一种差动变压器式位移传感器的建模仿真分析

郑西洋，许益民

（武汉科技大学 机械自动化学院，武汉430081）

差动变压器式位移传感器LVDT 是利用电磁感应原理来测量位移量，实现闭环控制的主要装置[1]，提高LVDT 位移传感器的灵敏度是改善高性能电液比例伺服阀设计的关键环节之一[2]，本文选择初级线圈长度、匝数，次级线圈的长度、匝数，来研究对输出电压的影响和对灵敏度的影响。

1 LVDT 的结构和工作原理

1.1 LVDT 的结构

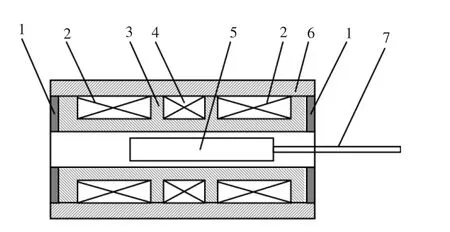
图1 LVDT 的结构Fig.1 Structure of the LVDT

LVDT 的结构如图1所示， 铁芯平时处在两线圈的对称位置上，使两边线圈的初始电压相等。当铁芯因被测物体位移在线圈里移动时，感应电压将反应被测物体的位移量的大小和方向。

1.2 LVDT 的工作原理

LVDT 线圈的内部是一个自由移动的柱状铁芯。当铁芯发生移动时，将引起线圈电感的变化，形成感应电压。图2为LVDT 的等效电路。

图2 LVDT 等效电路Fig 2 LVDT equivalent circuit

图中：U1、U2为初级线圈激励电压和次级线圈感应差值电压；E21、E22为次级线圈1、2 的感应电动势；L1、L21、L22为初级、两次级线圈电感；R1、R21、R22为初级、两次级线圈的有效电阻；M1、M2为初级与次级线圈1、2 间的互感。

2 LVDT 的建模仿真

2.1 建模仿真的参数设置

应用Ansoft Maxwell 对LVDT 进行仿真时，步骤如下：

步骤1LVDT 的等效建模。在进行仿真求解过程中，若所建模型与实际形状高度相符，则计算结果会更加准确。但实际操作中，受电脑计算能力的限制，在考虑计算效率的情况下，对模型进行合理的简化是必需的，也是必要的[3]。考虑到LVDT 为圆柱体结构，在不考虑结构误差和导磁不均匀的情况下，其内部磁场分布是均匀的，故可采用2D 模型代替3D 模型，且对仿真分析结果不会有太大的影响。

步骤2指定模型材料和定义磁化曲线。对于LVDT 瞬态电磁场分析，需要指定以下模型的材料，如表1所示。对于非线性的导磁材料，需要设置材料的BH 曲线。如图3所示。

步骤3添加外部电流激励。仿真时，为了让计算结果逼近实际，在仿真软件中选择外部电路激励，在ANSYS Electromagnetics 中使用Maxwell Circuit Editor 外部电路编辑专用软件添加各类元器件完成电路的绘制。如图4所示。

表1 模型的材料属性Tab.1 Material properties of the model

图3 BH 曲线Fig.3 BH curve

图4 LVDT 外部激励电路Fig.4 LVDT external excitation circuit

步骤4设置边界条件。LVDT 分析时，在LVDT的域外施加Ballon 边界即可。如图5所示。

图5 气球边界设置Fig.5 Balloon border settings

步骤5求解选项参数设置。在仿真软件中，执行Maxwell2 D/Analysis Setup/Add Solution setup命令，弹出求解设置对话框，如图6所示。本次仿真只针对一般设置与场信息保存进行设置，其他项均采用软件系统默认设置。在一般设置中，设置求解名称为setup1，设置求解终止时间为0.1 s。场信息保存时间步长设置为0.0005 s， 即场求解每2 步保存一次， 然后单击Add to List 按钮将具体设置增加到时间菜单中，具体设置如图7、图8所示。

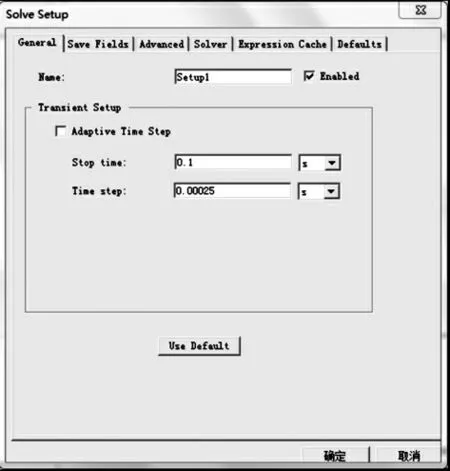
图6 计算参数设置界面Fig.6 Calculation parameter setting interface

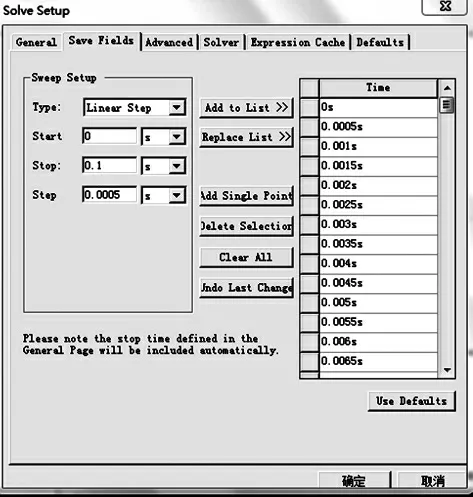
图7 设置求解步长Fig.7 Setting the solution step

2.2 仿真计算及后处理

根据之前叙述的工作原理可知，LVDT 中铁芯向两端次级线圈移动时的输出位移-电压曲线是关于Y 轴对称的，故在仿真计算时，只需进行，铁芯从中间位置向左端或右端次级线圈移动行程的求解，铁芯位移关系如图8所示。在铁芯从两端位置向中间位置移动时，输出电压与铁芯位移关系如图9所示。

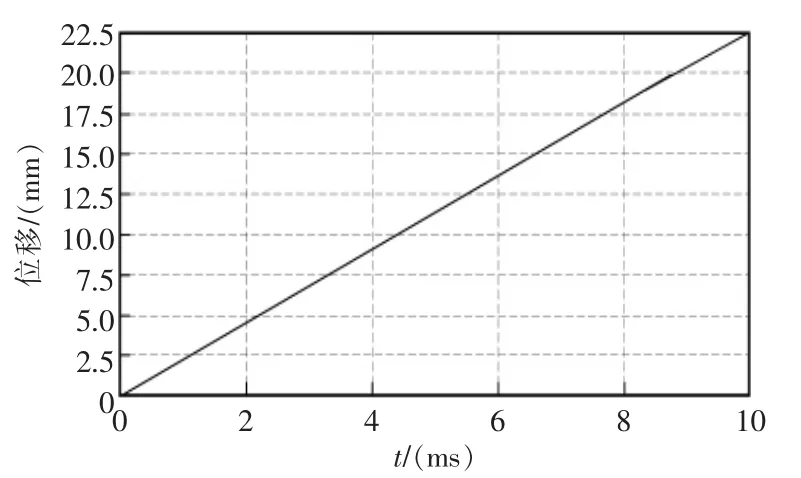
图8 铁芯位移关系Fig.8 Core displacement relationship

图9 输出电压与铁芯位移关系Fig.9 Relation between output voltage and core displacement

3 LVDT 的仿真结果及分析

Maxwell 是基于可视化操作交互式设置的电磁仿真软件[4]。同时，该软件的处理速度快，能快速进行有限元单元格剖分。有很多影响LVDT 灵敏度的因素，根据瞬态电磁场数值计算原理，在Maxwell 中建立LVDT 的二维仿真模型， 通过改变其结构参数和电气元件的数值进行仿真分析。在此，只分析结构因数的影响。

3.1 初级线圈长度对输出电压的影响

由于在电信号的激励下，随着铁芯的移动，输出电压也随之变化[5]。通过对仿真软件的设置，分别给定初级线圈为5 mm、15 mm、20 mm、25 mm、30 mm条件下， 位移为4 mm、2 mm、0 mm、-2 mm、-4 mm时，进行仿真求解，得不同位移量下不同初级线圈长度下的输出电压值，如表2所示。

表2 各位移量下不同初级线圈长度下输出电压值表Tab.2 Output voltage values for different primary coil lengths under various displacements

3.2 初级线圈匝数对输出电压的影响

通过对仿真软件的设置，分别给定初级线圈为600 匝、700 匝、800 匝、900 匝、1000 匝时，位移为4 mm、2 mm、0 mm、-2 mm、-4 mm 时， 进行仿真求解， 得不同移量下不同次级线圈匝数下输出电压值，如表3所示。

表3 各位移量下不同初级线圈匝数下输出电压值表Tab.3 Output voltage values for different primary coil turns under various displacements

3.3 次级线圈长度对输出电压的影响

通过对仿真软件的设置，分别给定次级线圈长度为20 mm、30 mm、40 mm、50 mm、60 mm 下， 位移为4 mm、2 mm、0 mm、-2 mm、-4 mm 时，进行仿真求解， 得不同移量下不同次级线圈长度下输出电压值，如表4所示。

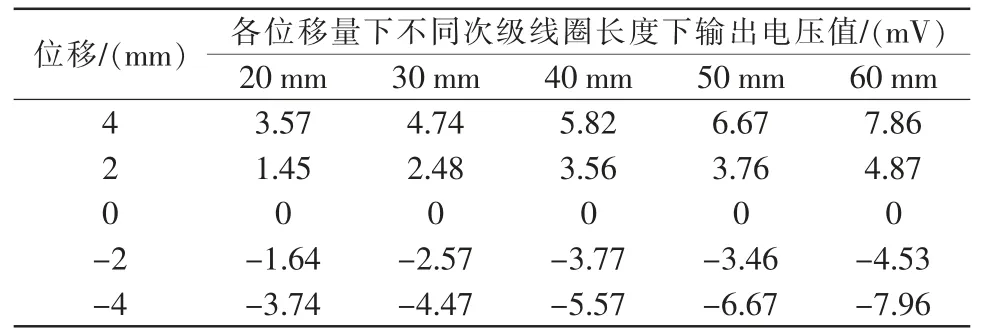
表4 各位移量下不同次级线圈长度下输出电压值表Tab.4 Output voltage values for different secondary coil lengths under various displacements

3.4 次级线圈匝数对输出电压的影响

通过对仿真软件的设置，分别给定次级线圈为600 匝、700 匝、800 匝、900 匝、1000 匝时，位移为4 mm、2 mm、0 mm、-2 mm、-4 mm 时， 进行仿真求解，得不同位移量下不同次级线圈匝数下输出电压值，如表5所示。

表5 各位移量下不同次级线圈匝数下输出电压值表Tab.5 Output voltage values of different secondary coil turns under various displacements

3.5 初级线圈长度、匝数与灵敏度的关系

对4 mm 至-4 mm 轴向范围的位移， 在初级线圈长度分别为10 mm、20 mm、30 mm、40 mm、50 mm，初 级 线圈匝 数 分 别 为500 匝、600 匝、700 匝、800匝、900 匝时的灵敏度，如表6所示。其灵敏度与初级线圈长度、初级线圈匝数如图10、图11所示。

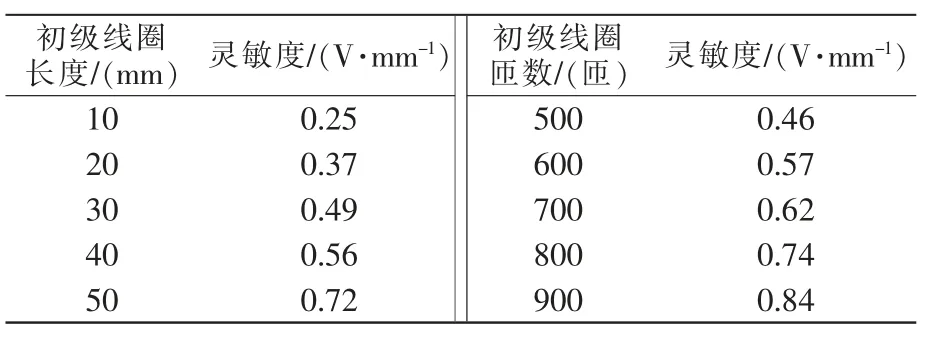
表6 初级线圈长度、匝数与灵敏度的关系表Tab.6 Relationships between the length，turns and sensitivity of primary coils

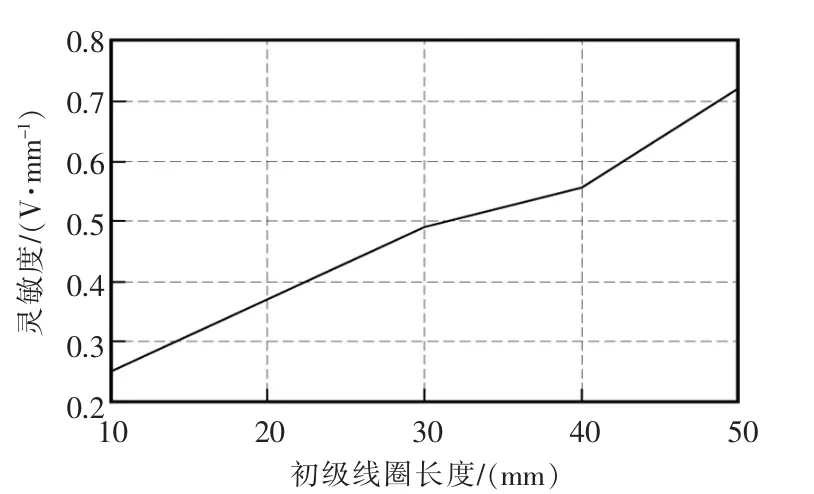
图10 初级线圈长度与灵敏度的关系Fig.10 Relationship between the length of primary coil and sensitivity

图11 初级线圈匝数与灵敏度的关系Fig.11 Relationship between the number of primary coil turns and sensitivity

3.6 次级线圈长度、匝数与灵敏度的关系

对4 mm 至-4 mm 轴向范围的位移， 在初级线圈长度分别为55 mm、65 mm、75 mm、85 mm、95 mm，初级线圈匝数分别为480 匝、580 匝、680 匝、780 匝、880 匝时的灵敏度，如表7所示。其灵敏度与次级线圈长度、次级线圈匝数如图12、图13所示。

表7 次级线圈长度、匝数与灵敏度的关系表Tab.7 Relationship between the length，turn number and sensitivity of secondary coils

图12 次级线圈长度与灵敏度的关系Fig.12 Relationship between secondary coil length and sensitivity

4 结语

本文通过建立LVDT 仿真模型利用Maxwell 进行了仿真分析，仿真结果表明随着初、次级线圈的长度、匝数增加，LVDT 的灵敏度逐渐提高，但由于在工程使用过程中受使用空间、材料成本和对实际使用精度的要求，LVDT 的初、 次级线圈的长度、匝数和整体尺寸应控制在合理范围内，才能满足实际市场要求。仿真结果对LVDT 的改进提供了参考依据，有助于LVDT 的结构改良设计，并具有一定的参考借鉴意义。

图13 次级线圈匝数与灵敏度的关系Fig.13 Relationship between the turn number of secondary coils and sensitivity