十年磨一剑——解码“集合问题”与“重叠问题”的教学理念

□ 高子林

2007年与2017年，笔者以同一内容先后参加教学比武，都获得了一等奖。不同的是，2007年以“集合”为题，2017年以“重叠”为眼。在教学改革风起潮涌的十年间，这两节课的设计分别反映了怎样的教学理念？有哪些变迁？笔者做了一番比较。

一、2007年，认知冲突中“了解集合知识”

（一）教学实录（部分）

师：（呈现材料）已知“班干部有9人，小组长有8人”，右边的小男孩却说“总人数没有17人”，难道求班干部和小组长的总人数不是“9加8”吗？

生：因为有些人是重复的，一个人做了两项工作，所以“9加8”是不对的。

师：“因为有些人一个人做了两项工作，所以总人数不能简单地相加”。你们同意这种观点吗？再想一想，同桌议一议。

生：最前面的3个人，他们既是班干部又是小组长。因此，总人数应该比17人少3人。

生：17人减去重复的3人，正好是我们班班干部和小组长的总数。

师：减3的道理是什么呢？

生：班干部里有这3个人，小组长里也有这3个人，“9加8”就多算了一个3。17人减去3人，正好把多算的去掉了。

师：大家说得很有道理。如果我用两个圈分别表示班干部和小组长的人员情况，怎样才能清楚地表示出“3人既是班干部又是小组长”？

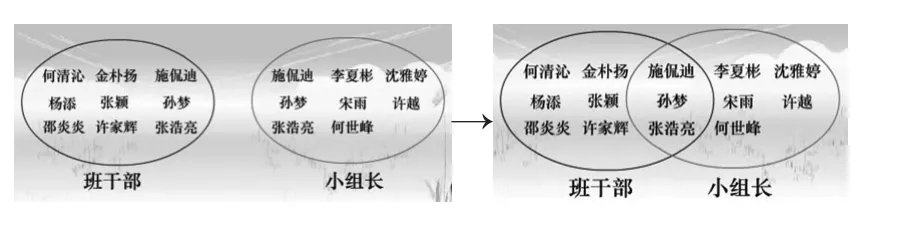
生：把重复的人连起来。（略）

生：把重复的人圈起来。（略）

生：（手势略）把两个圈重叠起来。

师：哪里重叠起来？

生：“既是班干部又是小组长”的那部分重叠起来。

（课件展示两集相交的过程，如上图右边）

师：哪部分表示班干部？哪部分表示小组长？哪部分表示既是班干部又是小组长？哪部分只表示班干部？哪部分只表示小组长？（生答略）

师：像这样的图，在数学中，我们把它叫作“集合图”。（板书：集合）

师：如图，已知班干部有9人，小组长有8人，既是班干部又是小组长的有3人，请你写出表示总人数的算式。

生：9+8-3=14。

生：6+5+3=14。

……

（二）解码教学理念

1.以“了解集合知识”为教学目标

2007年上“集合问题”一课时，实验版课程标准指导下的小学数学教材已使用3年，虽然有用“初步体会集合思想，解决简单实际问题”改进教学的声音，但实践中大多还是借鉴初中和奥数对“集合”知识的定位，仍然以“了解集合知识”为主要教学目标。

2.利用“认知冲突”发现“集合”的表征形式

笔者跟这个时期的大多数教师一样，忽视学生已有的知识经验、思想方法，教学设计以“教知识”为主。教学中通过呈现“班干部”和“小组长”的名单，设计了一个“班干部人数+小组长人数≠总人数”的知识冲突，使学生聚焦“有些人既是班干部又是小组长”这一“重叠现象”，进而引导学生“创造集合的形和式”。当时认为给“集合”套上一个背景故事就是在“解决问题”，就是在“发现数学思想”，实际上仅是用“圈”和“式”表征“重叠现象”而已。

二、2017年，解决问题中“体悟重叠思想”

（一）教学实录（部分）

师：（呈现材料）学校举行达标运动会，高老师派了5名同学参加跳绳比赛，6名同学参加跳远比赛，一共派了几人参加比赛？

生：5+6=11（人）。

师：（指下图）你说的是这个意思吗？

生：也有可能不需要11人……

师：“可能不需要11人”是什么意思？难道少派几人也能达到“5人参加跳绳比赛，6人参加跳远比赛”的效果？请像上图那样用画圈和算式来表达你们的想法。

（四人小组合作研究，并在纸上记录）

组1：有5人既参加跳绳比赛又参加跳远比赛，还有1人只参加跳远比赛，只需要派6人（如图1）。

组2：我们也是6人，但是画得不一样（如图2）。

图1

图2

师：还有派6人，但图画得不一样的小组吗？

（另两个小组出示作品，如图3、图4）

图3

图4

师：这些图都表示出了什么特点？

生：有5人既参加跳绳比赛又参加跳远比赛。

师：你们最喜欢哪个方案？（生答略）

师：（呈现图5）哪部分表示参加跳绳比赛的人？哪部分表示参加跳远比赛的人？哪部分表示既参加跳绳比赛又参加跳远比赛的人？5加6的结果为什么还要减去5？

图5

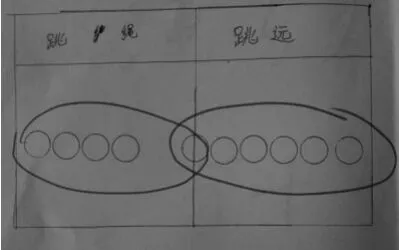
图6

（生答略）

师：还有其他方案吗？

生：1人既参加跳绳又参加跳远，总共派10人（如图6）。

师：算式怎么写？

生：5+6-1=10（人）。

师：还有其他想法吗？

（生出示如下作品，如图7、图8、图9）

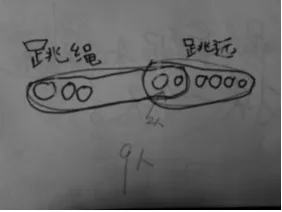
图7

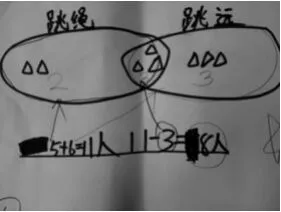
图8

图9

师：像以上这些问题，称为“重叠问题”。重叠问题有什么特点？怎么解决？

生：有一部分人既做这件事又做那件事。

生：总数里要去掉“重复”的部分。

……

（二）解码教学理念

1.以“体悟重叠思想”为教学目标

2017年上的“重叠问题”一课，是在2011年版课标指导下，体现了“人本主义”和“建构主义”，“了解集合知识”的教学目标已经退居后台，“通过解决问题体悟重叠思想”的教学目标进入了教师的视野和实践。

2.经历“解决问题”感受“集合”思想方法

跟十年前一样，这个时期的教学方案仍然有一个背景故事，但已经跟之前有了质的变化。如果说十年前的背景就是“交集现象”生活素材，那么十年后的背景真正是一个“解决问题”的开放场景：要派5名同学参加跳绳比赛，6名同学参加跳远比赛，一共要派几人参加比赛？这里既有如图10的已有集合经验的表达，又有如图11的未有经验的集合知识的呈现。

图10

图11

本课中，背景故事本身是一个需要解决的问题，既有“起点”（加法模型）又有“终点”（重叠问题），很有开放性和成长性。在这里，“集合思想”既是数学学习的对象，又是解决问题的方法，形象地讲，就是用“旧拐杖”做“新拐杖”，用“新拐杖”走“新路程”，实现从“A+B”到“A+B-C”的升华。

三、教学理念升华的意义和价值

2007年，教师把“集合”当成一种“新生事物”，以引导学生获取知识为主要目标。事实上，学生从入学开始就跟“集合”打上了交道，“加法就是求两个交集为空集的集合的并集的基数”。2017年这一课，学生通过某种途径“开放”了学习内容，“提升”了已有思想。从“集合问题”到“重叠问题”的演变，其意义和价值在于以下三个方面。

一、知识更具结构性

在“派人”这个真实情境下，学生既能展现原有“加法模型”，又能发现“重叠现象”，体现了集合思想的本质。由于新知识生长于旧知识，新思想升华于原思想，学习不是简单的顺应，而是结构性的“同化”，是在“搭积木”，便于记忆与迁移。

二、思想更具指导性

在解决问题的真实情境中，学生有意愿、有空间突破“A+B”加法模型的局限，去构造一个“A+BC”的重叠模型。“重叠问题”的思想，有效地拓宽了“求总数”的问题解决策略，让“A+B-C”这种重叠模型向下融合“A+B”加法模型，从而更具有解决问题的指导性。

三、学习更具挑战性

虽然2007年课的学习活动中，学生也有认知冲突，也有模型的建构过程，但完全没有2017年这一课学生在学习中的那种“解决问题”的冲动。“基于问题解决的重叠问题”的挑战性学习，是应用认知规律升华儿童认知的有效方式。

十年变迁，表面上看，那一头是知识为本，这一头是思想为要，但深层次上，它反映了小学数学界对学生数学学科核心素养培养的孜孜追求，是小学数学课程不断成熟的标志之一。