核心问题引领，把握运算本质——《分数乘整数》教学实践与思考

⦿徐玉平

计算教学是数学教学的重要内容，通过教学不仅要让学生掌握算法，更要促进思维的发展。引导学生理解算式的意义、尝试运算的方法，思考运算的道理，无疑是计算教学中，发展学生思维的三个主要切入点。基于这样的认识，几乎所有的计算教学初始课，都可以围绕着运算的意义、算法和算理这三个核心问题展开学习。这样的计算教学既简，又准，学生可以在自主探索中，打通不同运算之间的联系，深刻把握运算的本质，促进运算知识结构化，使思维走向通透。《分数乘整数》一课就是基于这样的思考，以“问题解决”模式展开的一次教学尝试。

【教学片段】

一、以旧引新，自主提炼核心问题

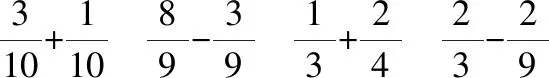
回顾：同分母分数加减法，怎样计算？异分母分数呢？计算结果要注意什么？师：我们已经会计算分数加减法了，你还想学习分数的哪些运算？生：分数乘法和除法怎么算。师：这节课我们就来学习分数乘法，先从分数乘整数开始。你能说几个分数乘整数的式子么？面对这种新的计算，你想研究些什么呢？生1：这些式子该怎么算？生2：这些式子表示什么意义？解决什么样的问题就要用这种运算？生3：我不仅想知道怎么算，还想知道为什么这么算？……师：同学们提的问题对于理解分数乘整数都很有价值。主要是这样三个核心问题：分数乘整数的意义、算法、算理。我们就围绕这三个问题展开探索和学习。

二、自主探索，初步理解乘式的意义和算法

学生独立列式解决，互相交流。：

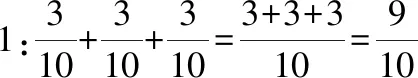
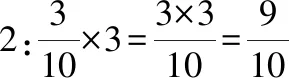
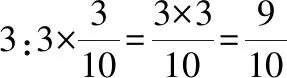
师：同学们能运用学过的整数乘法来解释新的分数乘法，真会思考！这两个乘法式子的计算过程有道理么？谁能解释解释。生1：可以用连加式子来理解：同分母分数相加，分母不变，分子相加。所以分母就是10，分子3个3相加，就是3×3。

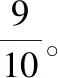
三、沟通比较，加深对乘式的理解

四、总结概括，回答三个核心问题

师：课一开始同学们提出来研究三个核心问题：分数乘整数的意义、算法和算理。通过刚才的学习，现在能回答这三个问题了么？可以在小组里互相讨论一下。生1：我们认为分数乘整数跟整数乘法本质是一样的，是求几个相同分数的和的简便计算。生2：我们总结分数乘整数应该这么算：分母不变，分子与整数相乘的积做分子，结果一定要是最简分数。生3：这样算是根据同分母分数计算方法来的：分母不变，分子相加。整数是几，就有几个分子相加，所以就用分子乘整数。师：分数乘整数的式子有很多，我们能不能用一个字母式子把总结的计算方法简洁的表示出来呢？

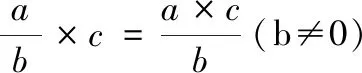
反思：

(一)核心问题引领计算教学，有利于“以生为本”的理念落到实处

意义、算法、算理这三个计算教学的核心以往都在教师心里，化成教学设计，最终促使学生掌握。基于问题解决教学的模式，把这三个知识问题化、显性化，课堂就一直围绕这三个问题反复展开思考，让学生深刻领会学习计算就是要探寻这三个问题的答案。把握住这一点，学生完全可以自主的进行计算知识的学习。没有了琐碎的提问，没有了亦步亦趋的引领，课堂上老师把探究的时间和空间让位给学生，既有学生的独立思考，又有生生之间交流碰撞，当然更少不了教师机智的适时介入，追寻的核心问题答案逐渐明朗，直至水落石出。这样教学，学生不仅能学到计算的知识，更能感受到自主探究的乐趣，体会思维豁然开朗的通透，这样的学习一定是有意义、有意思的。

(二)打通运算知识前后联系，有利于促进运算知识结构化

学生任何新知的学习都离不开相关的已有知识基础。要能真正掌握分数乘整数，必须打通与整数乘法以及同分母分数加法等知识之间的联系。事实上学生对分数乘整数的意义、算法和算理的理解，都是基于这些基础之上的。只要纳入了原有知识结构，学生就能领悟到所谓“新知”，不过是原有知识结构的不断生长扩充而已。不仅是计算教学，任何板块的教学，如果教师都能始终关注前后知识的联系，以知识系统的整体性、关联性、结构性指导教学实践，那么学生的基础学力和数学素养一定能得到有效的培养。数学在学生眼里不再是枯燥的知识叠加，而是有趣的沟通生长，相信会有更多的孩子爱上数学。