强化运算素养 提升思维品质*——以椭圆中的运算为例

高新柠 郭建华(指导教师)

江苏省南京市第二十九中学 (210036)

解析几何的运算给人们的感觉是繁琐，有的同学遇到解析几何问题就会感到畏惧，不敢去算，也不愿意去算，或者是没有掌握运算的技巧和方法，算不下去，于是导致解析几何题得分较低，因此，很有必要在平时的训练中加强对解析几何题的各种题型进行归类和反思.尤其对解析几何题要在运算上多下功夫，因为它是解决问题的基本手段.其实数学运算主要表现以下四个方面：理解运算对象，掌握运算法则，探究运算思路，求得运算结果.通过椭圆中运算的培养，进一步发展数学运算能力，不断促进数学思维的发展，提升规范化思考问题的品质.下面通过例题浅谈一下解析几何运算中思维品质的提升.

1.理解运算对象，提升思维的敏捷性

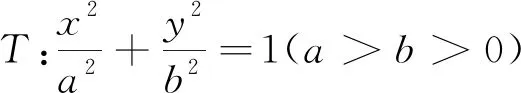
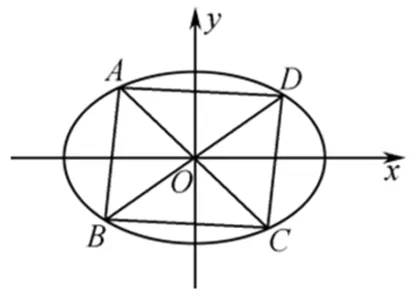
图1

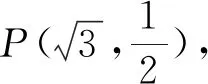
(1)求椭圆T的方程；

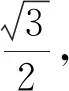
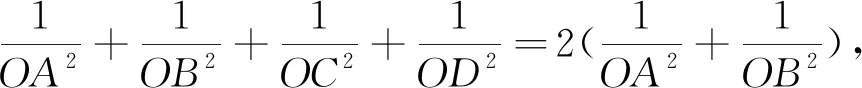
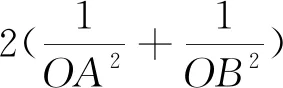
2.探究运算思路，激活思维的灵活性

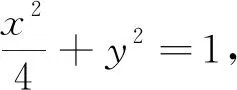
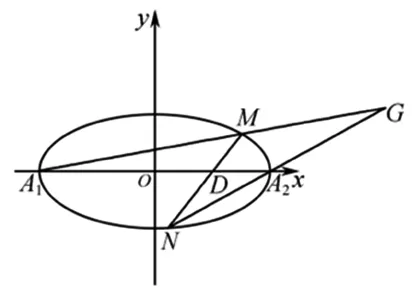
图2

证明：(方法1) 设直线A1M的方程为y=k1(x+2)，直线A2N的方程为y=k2(x-2)．联立方程组

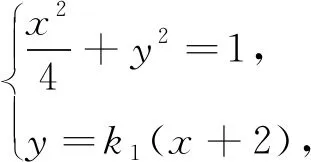
下面证明对于任意的实数m，直线A1M与直线A2N的交点G均在直线x=4上．

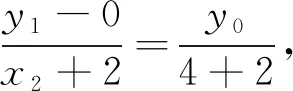
点评:思维的灵活性是指思维活动的灵活程度，善于根据事物的发展变化，及时地用新的观点看待已经变化了的事物，并提出符合实际的解决问题的新设想、新方案和新方法.也就是能从不同角度观察、不同层次思考、利用不同方法依据新的条件迅速确定探究运算思路，探寻解决问题的最优方案.证明思路1通过设直线A1M与直线A2N的方程求解点M,N的坐标，再利用M、D、N三点共线找出k2,k1关系，从而得证，在运算上较为繁琐；由于要证明的目标很明确，因此思路2选择特殊法处理，其实这是优先考虑的一种解法.另外根据直线MN过x轴上的定点，设其方程为x=my+1，这样不仅提高了解题的速度和准确度，而且降低了思维的难度.在椭圆的运算中要从不同角度分析问题，加强解题方法的对比，才能探寻到更好的求解方案，更有利于培养思维的灵活性.

3.选择运算方法，培养思维的独创性

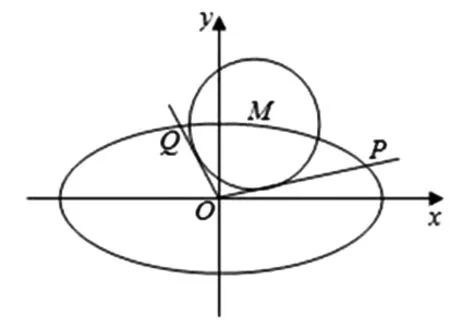
图3

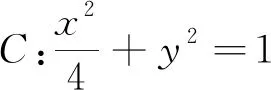
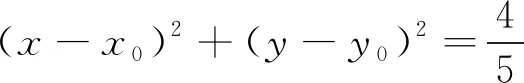
(2)求OP·OQ的最大值．

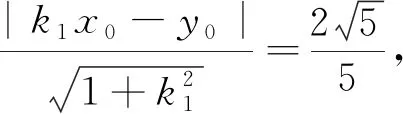
(2)设P(x1,y1),Q(x2,y2)，联立

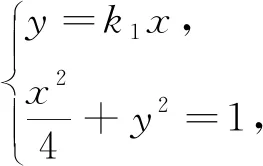
算法1 由于目标函数为齐次式，先将其进行常数分离，再用基本不等式求解.

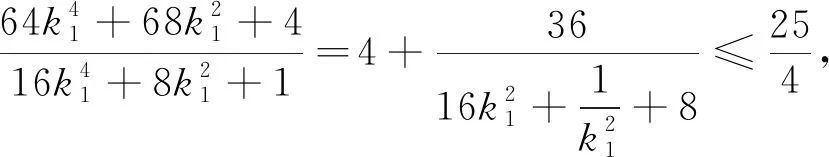
算法2 利用换元法，再结合二次函数求解.

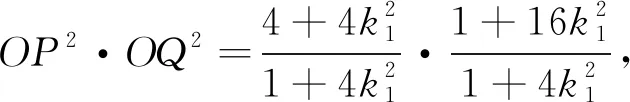
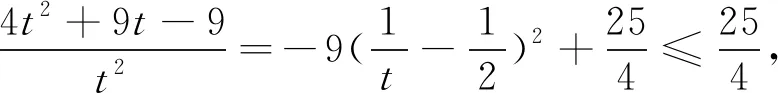
算法3 通过分析、观察分式目标函数的结构，对分子用基本不等式求解即可.

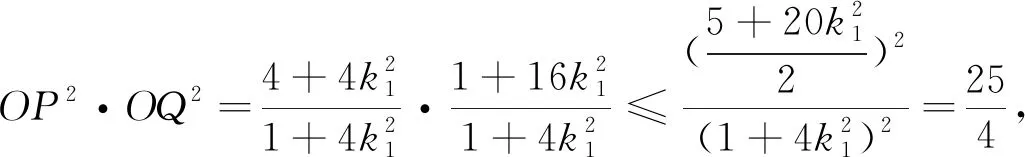
算法4 采用先特殊后一般的方法，再结合基本不等式求解.

(1)当直线落在坐标轴上时，显然有OP2+OQ2=5；

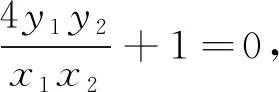
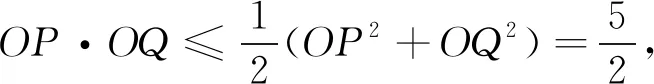
点评:算法1和算法2都是常规方法，运算较烦，算法3最简洁，需要很强的观察力，算法4先特殊后一般，也是处理解析几何的常用方法.椭圆中分式求最值问题是很繁琐的，要想更快的求得运算结果，必须学会选择最优的运算方法，在方法的选择和比较中会不断的发现问题、提出问题，才会在解题中养成更全面、深刻、完整的思考问题的习惯，才会在新情景中采取新对策培养分析问题和独立解决问题能力，进而培养思维的独创性.

4.求得运算结果，提升思维的深刻性

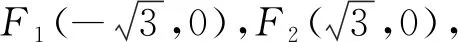
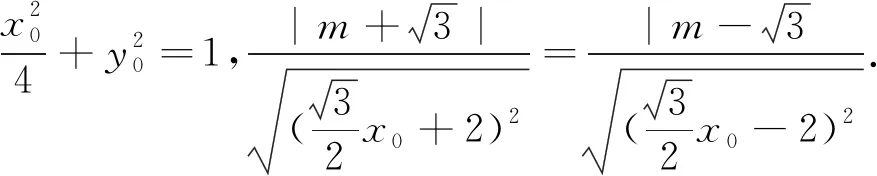
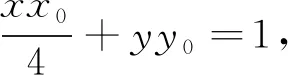
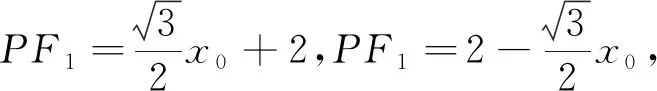
点评:思维的深刻性是指能深入到事物的本质里去考虑问题，它是以思维的批判性为前提的.三角形内角平分线的性质是本题考察的核心，也是求解该问题的切入点，也为在关联的情景中准确确定运算对象，运算法则和明确运算方向提供前提.解法1是利用其对称性求解，运算繁琐，解法2是在综合情景中联想到光学性质求解，利用椭圆的切线方程迅速求得结果，解法3借助于焦半径和角平分性质求解也是一个很好的选择，在求得运算结果的过程中，加深问题的深刻理解，把握问题的本质内涵，选择灵活的方法，发散思维，让思维在解题中真正发挥作用.

总之，在处理椭圆的典型运算问题时，不仅要掌握算法，而且要明白算理，在运算上多下功夫，对一道典型的问题要深入研究，探究解法的多样性，加强运算素养的培养，从而提升思维的品质.