单元复习课教学中存在的问题与建议——以《数列》单元复习为例

丁益民

江苏省苏州实验中学 (215011)

最近，笔者参与了我区招师活动的课堂教学考核环节，教学内容为苏教版·必修5教材(下称教材)数列单元复习课，从参与应聘的30位教师的课堂展示情况来看，发现很多教师并没有准确认识单元复习课的教学功能.为什么要上单元复习课？学习论认为，经过一阶段的新课学习，学生获得的是一些简单概念和单一的解题技巧，对这些零散的点状知识容易产生遗忘和混淆.因此，需要对已学知识进行梳理与整合，单元复习是将本单元的相关知识进行梳理、归类、巩固，理清知识间的逻辑关联，构建出系统的知识网络，从单元的角度理解数学知识.

一、单元复习课教学中的存在问题

从应聘教师的课堂展示可以看出当前有些教师对单元复习课的课型功能认识并不准确，或上成知识罗列课，或上成解题教学课，或上成专题复习课，给人一种简单堆砌、偏离目标之感.主要存在以下问题：

问题1 教学达成目标的层次偏低

一些教师在制定单元复习课的教学目标时，简单地将本单元各课时目标进行汇总，更多关注知识点的“全”，却不能整合知识点间的逻辑要素，导致单元复习成了一种“炒冷饭”式的知识点回顾，课堂教学始终在低位目标徘徊.

很多教师在知识回顾时都采用“数列的定义→数列的通项公式→等差数列的通项与求和→等比数列的通项与求和”的复习线路，这样的过程就是单纯地按照知识顺序进行无意义的回顾，并不能帮助学生形成上位的整体认知，这样复习的效果自然不够理想.实际上，根据学生已有的认知，提炼出知识间的逻辑主线，将整章内容串联到这样的逻辑主线中去，从整体上形成知识的逻辑架构.

问题2 教学处理的深度不够

有些教师在单元复习时中只关注识记性知识和程序性知识目标的落实，却对基本数学活动经验的构建、重现以及关键能力的培养不予重视，导致课堂教学的深度不够.

如有些老师都选择教材P68第12题作为“错位相减法”的复习载体：

题目 已知等差数列{an}满足a2=0,a6+a8=-10.

(1)求数列{an}的通项公式；

绝大部分老师是这样处理的：引导学生分析问题(2)中的处理方法(错位相减法)后口头强调该法容易出错，却鲜有老师将本题的完整过程重现出来.学生在没有切身体验下的认知是不深刻的，口头强调式的教学手段并不能强化学生认知结构中的活动经验.

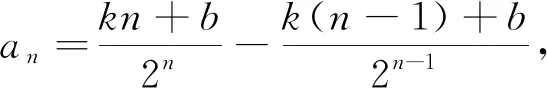
问题3 组织方式比较低效

单元复习课中常见的教学组织方式有两种：一是讲知识点为主，把本单元所有知识点罗列在一起，重新再讲一遍，这种直叙式的组织形式让学生觉得索然无趣，效果可想而知；二是讲题为主，根据本单元知识点选择一些习题让学生练习后再讲评，这种组织形式没有依据学生的实际认知，复习并没有针对性.

师1的组织方式：

习题1：……知识点拨1：……

习题2：……知识点拨2：……

师2的组织方式：

知识提要1：…… 习题1：……

知识提要2：…… 习题2：……

以上两位老师的教学组织都没有关注知识、能力与经验的内在关联，无助于学生构建单元的知识、思维能力和数学活动经验体系.其实，可以将上述教学组织中“知识点拨”、“知识提要”设计为“知识梳理”，再引导学生独立完成、交流完善，从中体现习题间的逻辑关联和层次性.

二、单元复习课的教学建议

1.准确认识“本章回顾”的设置意图

为了减少单元复习的随意性和盲目性，教材在每章末都设置了“本章回顾”.主要包括：知识结构，学习要求(包括知识、技能、思想方法)以及内容提要.在知识结构的呈现方式上采用的是框图形式，直观形象地反映了知识的来龙去脉，并且框图可以进一步开发整合(比如常可拓展成思维导图).学习要求不同于课时要求，是对整个单元的宏观要求，内容提要则采用提纲形式将本章主要内容予以回顾，目的是抓住主干知识，舍末求本，其目的是防止扩张教学范围，杜绝深挖教学内容，这是单元复习的行动纲领.

就“数列”一章而言，在复习时应引导学生从两个认知视角进行梳理，一是函数视角，数列是以“数”为研究对象的特殊函数，整个数列教学体系中，应始终以函数的视角来审视数列的性质，比如数列中的项是如何变化的(如单调性)？数列的项与项之间有怎样的关系(递推关系)？等等.另一个是运算视角，即建构合适的运算规则来研究数列中的运算，比如，通过“累加”的运算方式得到等差数列的通项公式，进一步地这样的运算规则还适用于形如递推关系“an-an-1=f(n)”的通项公式求解问题.以这两条线索可进行以下梳理：

函数视角

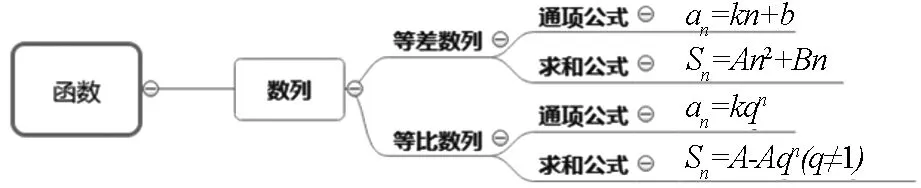
运算视角

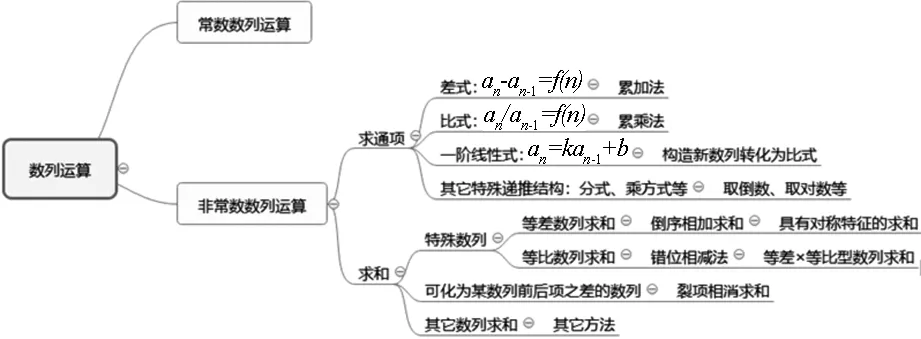
通过从这两条认知视角来整合已学内容，形成新的认知块，加深知识的关系系理解，促进深度理解.

2.实施有效的教学组织

教学组织方式决定了单元复习的质量，单一罗列知识和逐一讲解例题的实际教学效果往往高耗低效，学生的数学理解水平淹没在题海之中.在复习时可以围绕核心概念展开，引导学生运用已有知识来论证核心概念；或者寻找支撑核心概念的一般概念与相关具体问题，试图对原有知识进行必要的拓展与深化，建立起知识间的逻辑联系，并确定知识的运用范围，实现知识的深度理解.

导学模式是进行单元复习时十分有效的组织形式之一，将复习内容以问题的形式呈现出来，问题可由学生先行解决.问题设计时要关注问题的起点、层次与跨度，起点不宜太高，适当高于新授课要求，逐层推进，思维跨度不宜太大，要具有一定的启发性与针对性，通过问题链着力构建出完整的知识框架.

要提高学生在解决问题时目标任务的达成度和效度.在“前置练习”中设置有关核心概念、重要性质的基础题，通过前置练习梳理出相关概念与性质，进而拓展出与之相关的外延知识.在此过程中那些无关紧要的知识坚决舍去(如等差数列的某些识记性的结论)，抓住重点，摈弃杂质，太多太空的结论性知识易将学生带入务虚空洞的知识梳理，这样就成了无意义的数学活动.梳理出的知识应与选择的例题相匹配，例题讲评的目的是加深核心知识的理解.最后再对整节课的进行小结.所以，整节课就是核心概念主线下进行的教学组织.

3.精心选编适合学生的典型例题

单元复习课离不开例题的选择与讲评，很多老师在单元复习时完全照搬高三复习资料中的成品例题，这就导致教学起点过高，教学难度过大，发生了教学重心偏移，起不到应有的复习效果.因此，在选题时要有一定的针对性、适度性和思考性.实际上，教材中有很多典型且适合学生认知特点的典型例题，可以借助这些例题进行复习提升.

如教材P68第17题：在等差数列{an}中，已知Sp=q,Sq=p,(p≠q)，求Sp+q的值.

很多老师在讲评此问题时仅仅将之定位成一个“结论”让学生记住，其实这道题的教学功能很多.

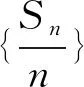
由此可见，选择合适的例题并从整体性中寻找问题解决的要素，对学生的思维训练与能力提升是有益的.

单元复习课教学研究任重道远，针对不同的知识类型，不同的学生群体，探索出适合的单元复习课教学模式和教学策略，提高单元复习课的教学深度，促进学生思维水平的发展和知识的理解深度.