直线与椭圆、双曲线相切的性质探究
2019-06-11 12:34:30龙光鹏涂燕青
中学数学研究(江西) 2019年5期
龙光鹏 涂燕青
江西省南昌市第十五中学 (330039)
1.源由
我们知道直线和圆相切的一条性质是:若直线与圆相切,则圆心到直线的距离等于圆的半径.同时,我们也知道当椭圆的离心率e接近0时,其形状越接近于圆.换而言之,圆可以视为一种“特殊的椭圆”.然而,有一个困惑顿时在笔者脑海里浮现:直线与椭圆相切时,有关距离会有哪些结论呢?
2.探究
2.1 直线与椭圆相切的性质
我们知道,椭圆的中心到椭圆的切线的距离是变化的,当椭圆的离心率e接近0时,即椭圆的焦点无限靠近椭圆中心时,椭圆趋近于圆,故探究椭圆的两个焦点到椭圆切线的距离会存在什么结论.
以焦点在x轴上的椭圆为例:
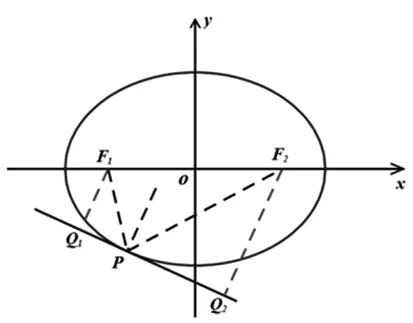
图1
首先,尝试直线l为特殊的切线x=a,则d1=a+c,d2=a-c,故d1+d2=2a,d1·d2=a2-c2=b2.
其次,尝试直线l为另一条特殊的切线y=b,则d1=b,d2=b,故d1+d2=2b,d1·d2=b2.
于是形成了一个猜想:当直线l与椭圆相切时,必有2b≤d1+d2≤2a,且d1·d2=b2.

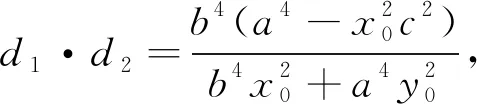
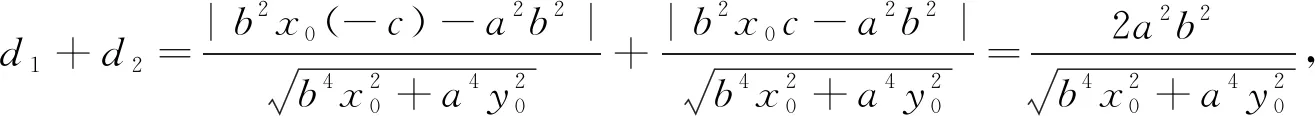
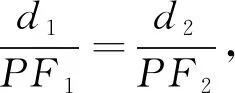
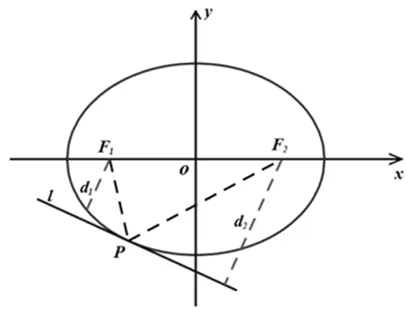
图2

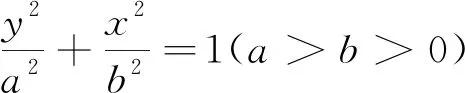
2.2 直线与双曲线相切的性质
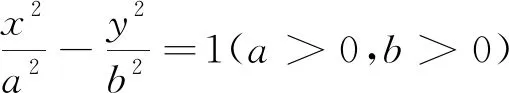
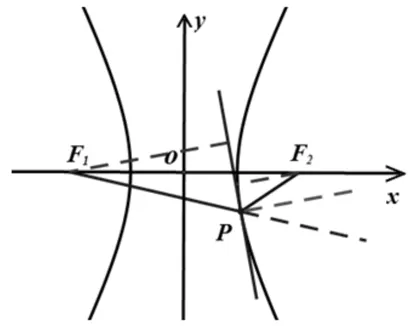
图3
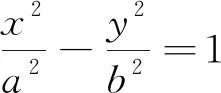
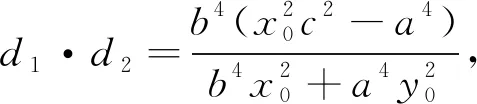
(Ⅱ)由双曲线的对称性,不妨假设点(x0,y0)在双曲线上的右支上,∴d1+d2
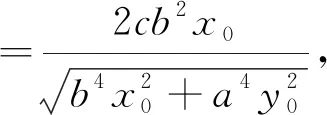
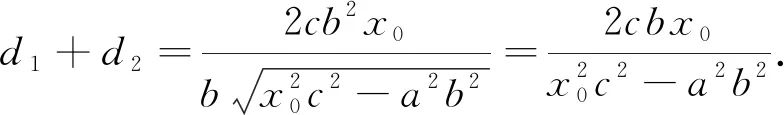
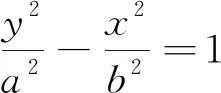
3.应用
笔者以上述的性质为基础,尝试编创以下2道试题:
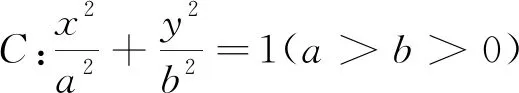
(Ⅰ)若过点A的直线l与椭圆C有且只有一个交点,求直线l的方程;
(Ⅱ)若点P是椭圆上任意一点,过点P的直线m与椭圆相切,求证:焦点F1,F2到直线m的距离的乘积为一个定值,并求出这个定值.
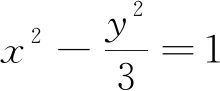
(Ⅰ)若过点M的直线与双曲线相切,且交x轴于点Q,求证:∠F1MQ=∠F2MQ;
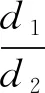
猜你喜欢
中学生数理化(高中版.高二数学)(2021年2期)2021-03-19 08:54:12
新世纪智能(数学备考)(2020年12期)2020-03-29 02:15:34
河北理科教学研究(2020年4期)2020-03-09 03:34:52
课程教育研究(2017年26期)2017-08-02 08:56:02
中学生数理化(高中版.高二数学)(2017年1期)2017-04-16 05:33:43
高中生·天天向上(2016年8期)2016-11-22 09:22:46
中学数学杂志(2015年9期)2015-01-01 09:00:16
今日中学生(初三版)(2013年6期)2013-07-30 06:29:40
好孩子画报(2013年5期)2013-04-29 14:14:00
中学生数理化·高二版(2008年11期)2008-06-17 09:25:42

