带有弹性网络惩罚的自适应多项式回归学习机及其特征选择性能

王小玉，贾 杰，常明明

(1.郑州工商学院 公共基础教学部，河南 郑州 450001；2.河南师范大学 数学与信息科学学院，河南 新乡 453007)

0 引言

逻辑损失函数在数学上具有二阶可微的特点，同时在统计学方面应用意义较为良好，从而使得正则化的逻辑回归模型在二分类以及多分类问题中具有广泛的应用[1-5]。

在解决二分类问题的过程中，通过结合不同的损失函数以及惩罚函数，可以形成不同优化性能的模型，从而解决二分类问题中的稀疏性问题。文献[1]通过将逻辑回归损失与L2范数惩罚函数结合起来，提出了一种正则化逻辑回归模型，该模型可以产生离散因子，又能准确描述重要的基因及其内在结构。通过从平衡数据集中提取相关的训练样本，文献[2]提出了一种新的混合k-mer逻辑回归模型，该模型潜在的显示出了不同基因所携带的DNA序列特征。利用引入内点的方法，文献[4]提出了一种新的L1正则化逻辑回归，并以此为依据，证明了L1正则化逻辑回归方法，在稀疏性能方面更优于其他模型。通过将逻辑回归与L1/2范数惩罚函数相结合，文献[5]进一步提出了稀疏性能更优异的逻辑回归模型。

若将逻辑回归函数推广并应用于多分类问题中，就转化为多项式回归模型问题。由于微阵列技术可以生成的样品数量相对较少，而且每一个样品都包含有成千上万个基因，因而产生的结果就是，基因数目远远多于样本的数量。因此，严格进行特征识别是微阵列数据多分类研究的一大特点[6-8]，而稀疏的多项式回归模型的产生，为此类问题提供了合理的应用及方法。通过构造出具有soft-max连接函数的泛化线性函数，文献[6]提出了一种稀疏多项式逻辑回归模型，该模型采用了拉普拉斯算子，因此大大提高了自身的稀疏性能。利用带有高斯潜在变量的数据增强的方法，文献[7]提出了一种变异的贝叶斯多项式概率回归模型，该模型的特点是可以减少预测中误差。通过引入弹性网络惩罚，文献[8]提出了一种相关突变的正则化多项式回归模型(Correlated Mutations via Regularized Multinomial Regression)，简称RMRCM，将该模型应用于蛋白质多重序列比对中，可以有效的确保在多重序列数据中预测链数目的有限性，防止过度预测情况的发生。基于上述思想，并结合多类自适应弹性网络惩罚函数本身具有自适应群体基因选择性能的特点，我们将多类自适应弹性网络惩罚函数与多项式似然损失函数拟合，从而得到了一种新的自适应多项式回归学习机。

1 问题描述

(1)

对于二分类问题中通常的线性回归模型，输出响应Y能被预测为：

(2)

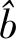
其中，偏差向量用b=(b1,…,bK)T表示，参数矩阵用w表示，即：

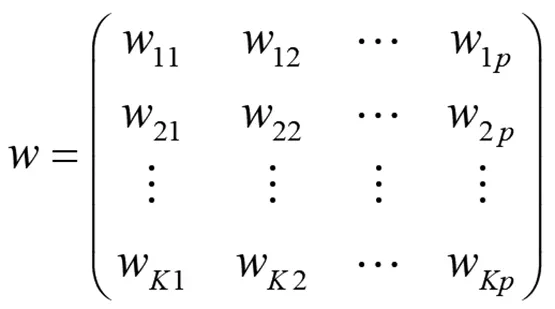
其中wk=(wk1,…,wkp)T和w(j)=(w1j,…,wkj)T分别表示参数矩阵w的第k个行向量和第j个列向量。从而上面的线性逻辑回归函数可形成一个多分对数模型。

现将其推广为K个分对数的情形。那么就可以得到通项公式：

(3)

其中(bk,wk)表示对应于样本(Y=k|x)的一对参数，bk∈R1,wk∈Rp。多分类问题中，已知类条件概率为：

(4)

建立模型，首先我们利用正则化的多项式似然函数,拟合前面所提出的已知类条件概率模型。即pk=Pr(Y=k|xi),yi∈{1,2,…,K}分别表示第i个响应值。则有：

令Y表示n*K阶的响应矩阵，其中的元素为yik=I(yi=k)，即：

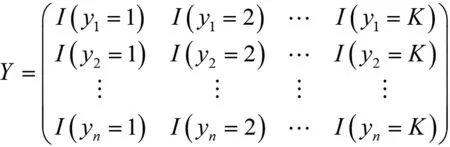
由于logpyi(xi)<0，我们选择-logpyi(xi)做损失函数。即：

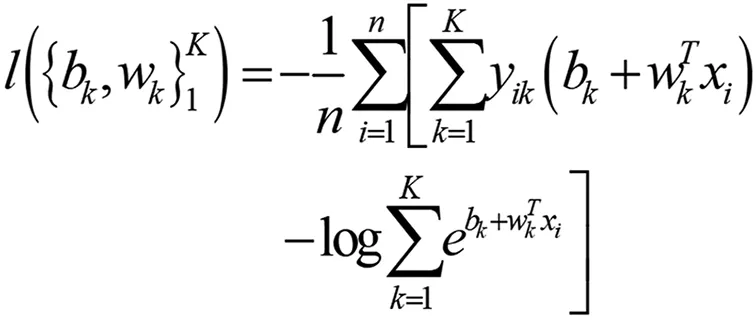
(5)

其中yik=I(yi=k)即：

yik=I(yi=k)={1,yi=k0,yi≠k

2 自适应多项式回归模型

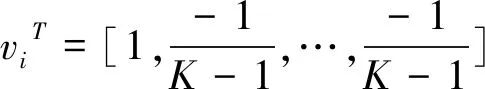
其中k=1,2,…,K,j=1,2,…,p

因此，多分类弹性网络惩罚可以表示为：

(6)

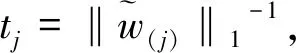
然而在上述过程中，我们发现，对应非重要基因的惩罚因子较大，而对应重要基因的惩罚因子却较小，由此产生的结果使得在实际应用会形成较大的误差。

改进模型的过程中，我们通过将上述自适应弹性网络惩罚函数，应用于多项式损失函数中，提出了一种新的自适应多类多项式回归模型：

(7)

s.t1Tb=0,1Twj=0,(j=1,2,…,p)

3 自适应群体基因选择效应

微阵列分类研究中，识别数据中相关的基因是非常重要的。而自适应多类多项式回归模型中，所有对应基因j的参数可以采用相同的权重tj。由于加权的L1惩罚的意义在于自适应的将所有对应于不重要基因的参数收缩为0，与此同时，可以减小对应重要基因的参数偏差，从而产生良好的稀疏性能。加权的L2范数惩罚的意义在于通过估计K类分类的重要性的基因排序来成群的选择基因。接下来，我们将通过下面的定理1，证明所给自适应多类多项式回归模型，在实际应用中可以进行群体基因选择，从而达到在基因群组中成群的辨识重要基因的效果。

首先，化简模型。将约束条件代入自适应多类多项式回归模型(7)，可以化简得到：

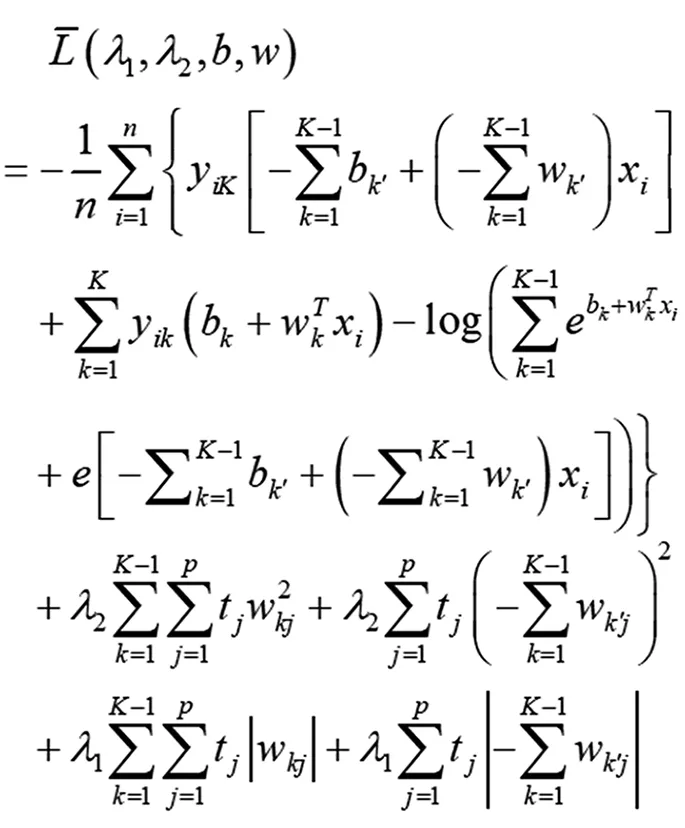
(8)

(9)

证明：首先，构造向量和矩阵指标如下：

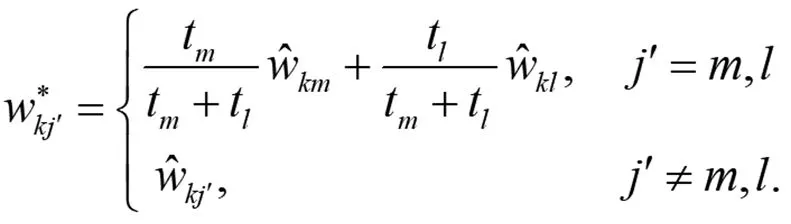
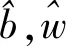
(10)

注意到Lki满足利普希茨条件，从而有：

运用反证法，易证不等式

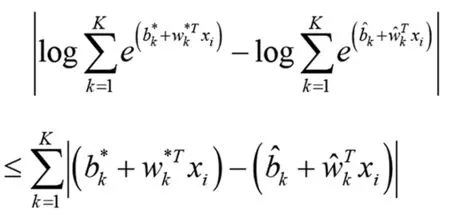
(11)

成立。因此可得:

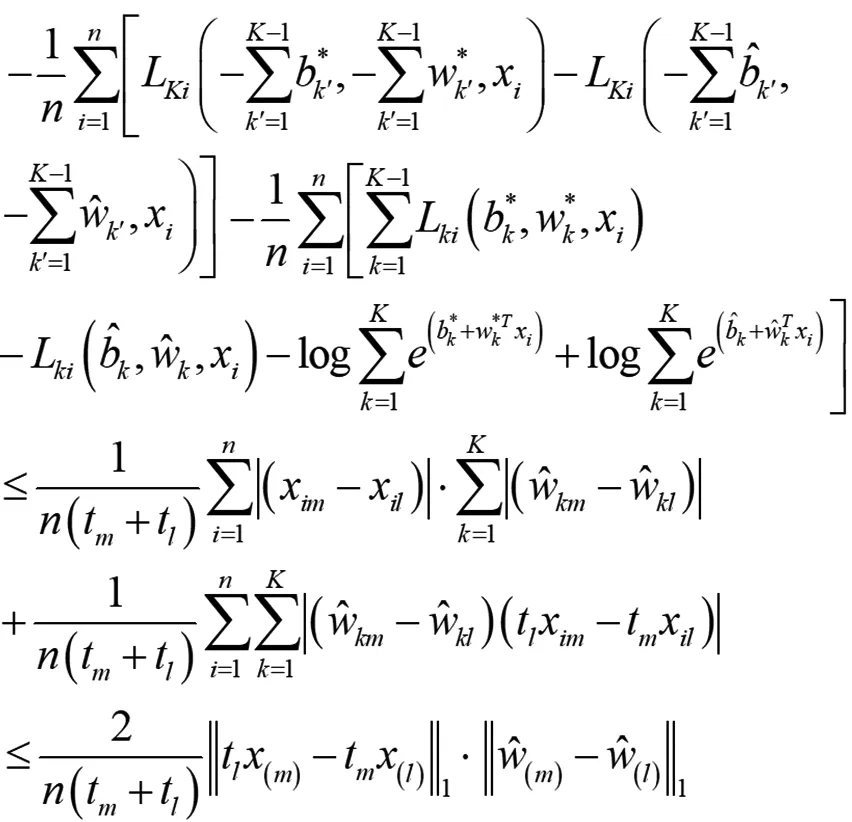
(12)

放大惩罚函数，从而一范数惩罚项可化为：

(13)

二范数惩罚项可以转化为：

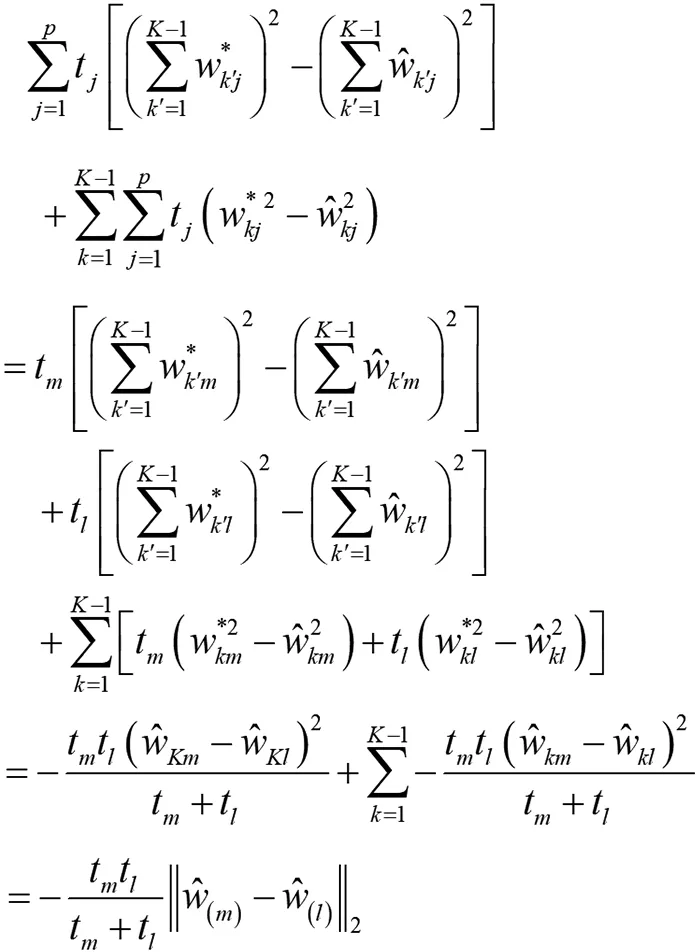
(14)

结合(10)，(12)，(13)，(14)可得：

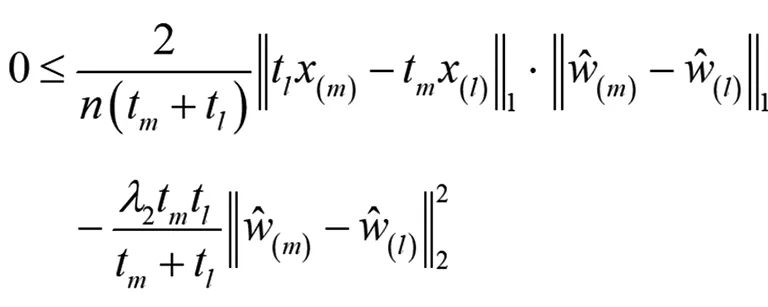
(15)

即：

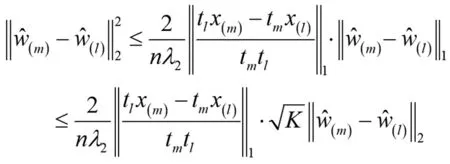
(16)

等价于：

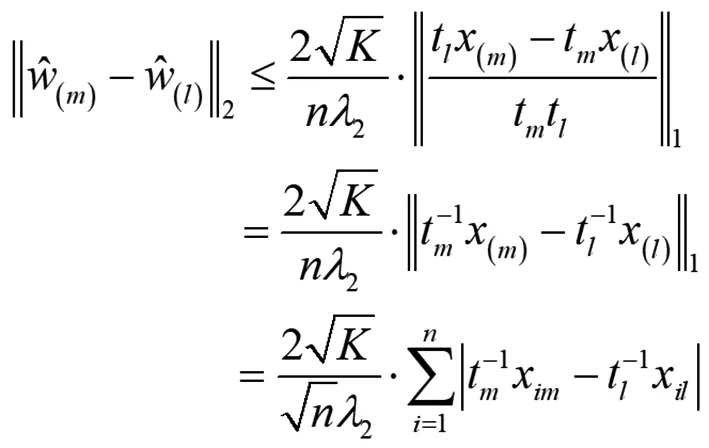
(17)

(18)

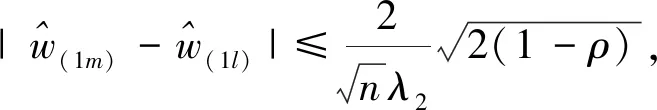
求解算法：我们在这里选用顺向坐标下降算法来求解上述自适应多项式回归模型。解决步骤如下：首先，将模型转换为：

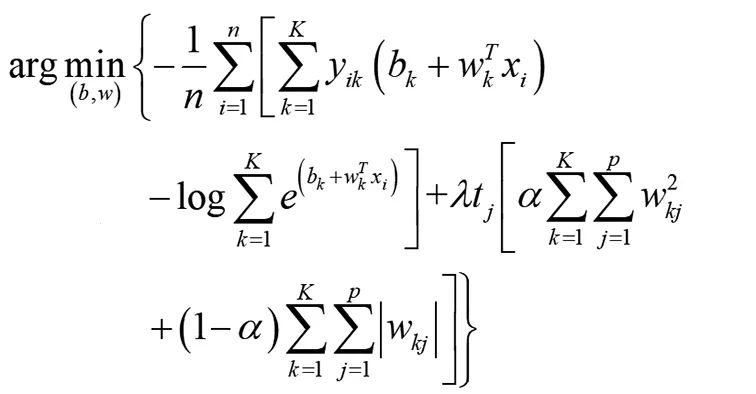
(19)

然后固定参数α，在参数λ的取值范围中计算正则化路以求解自适应多项式回归模型关于参数的解路。通常在解决线性回归或者多项式回归问题的过程中，针对常见的惩罚函数分别为L1范数和L2范数惩罚或者弹性网络惩罚函数类的模型问题，通常选择使用坐标下降算法。该算法可以应用于大型数据集如微阵列数据，通过利用特征集合稀疏性的优势以及顺向坐标下降算法来计算正则化路的方法，可以快速并有效地求解弹性网络的相关模型。

逻辑回归模型在二分类问题以及多分类问题中有着广泛的应用，但是该模型存在一定局限性。针对这一问题，本文通过在模型中引入具有自适应群体基因选择性能的多分类自适应弹性网络惩罚函数，提出了一种新的自适应多项式回归学习机器，并且证明了该学习机器可以在构建分类器的过程中有效地激励群体效应，并成群地选择相关的重要基因。