Haar小波求解时间-空间变系数分数阶偏微分方程

许海山

(郑州理工职业学院,河南 郑州 450000)

[关键字] Haar小波;算子矩阵;阿达马乘积;变系数;分数阶偏微分

0 引言

分数阶微积分作为对整数阶微积分的扩充,在物理、化学、生物和流体力学等学科领域有着非常重要的应用。因此,分数阶微积分受到越来越多数学家和物理学家的关注,这也在一定程度上推动了分数阶微积分理论不断地完善和发展[1]。分数阶微分方程的优势在于它能更精确的描绘自然界的动态系统过程。但一般情况下,我们很难直接求得分数阶微分方程的解析解,因此获得其数值解具有一定的理论意义和应用价值。在此之前很多学者对分数阶常微分方程、偏微分方程、积分方程提出了很多数值解法,比如分离变量法﹑同伦摄动法﹑有限差分法等[2-4]。

近年来,小波理论作为一门新兴的数学理论,在计算数学中在逐渐受到关注。小波是一种满足特定性质的函数,已被广泛应用于信号分析、图像处理、数值计算、信号处理等诸多方面[5]。在数值计算方面,其主要研究给定函数的近似表示,即把函数表示成一组“基函数”之和,这组基函数称之为小波函数。而近来,小波函数被用来求解分数阶微分方程。根据不同的函数性质,主要用到的有Haar小波[6-7]、Legendre小波[8]、Chebyshev小波[9]等，其中,最简单、最实用的小波是Haar小波。Haar小波具有形式简单、操作方便、相互正交等特点,使得人们通过分解系数刻画函数时,可以分析函数的局部性质和整体性质,有利于高效地得到高精度解。

利用Haar小波函数相关性质与算子矩阵思想,考虑下述形式系数为时间-空间变量的分数阶偏微分方程:

(1)

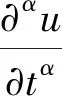
1 预备知识

定义1.1:Riemann-Liouville分数阶微积分定义分别为[1]:

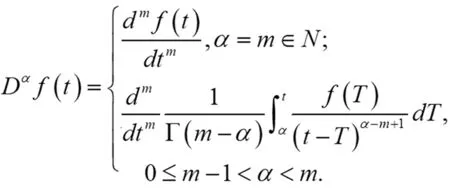
(2)

(3)

定义1.2:Caputo分数阶微分定义为[1]:

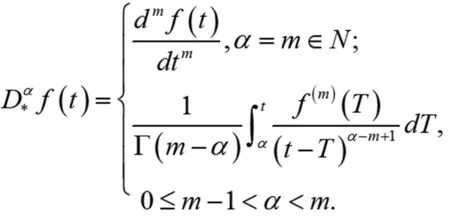
(4)

Riemann-Liouville分数阶积分与Caputo分数阶微分的关系如下:

(5)

定义1.3:Haar小波在t∈[0,1]定义为:

(6)

(7)

其中,i=0,1,2,…，m-1,m=2l,t是正整数,j,k表示i的整数分解,即i=2j+k-1。

2 算法的提出

Chen和Hsiao[10]在1975年提出了算子矩阵思想,Wu等[12]给出了一般意义下的积分算子矩阵。即对矩阵φ(t)的积分可近似表示为

(8)

其中Qφ为φ(t)的一重积分算子矩阵,可以推导得到φ(t)的n重积分算子矩阵Qφn。Wu等[11]给出了求任意矩阵在不同基下的积分算子矩阵的方法。

如φ(t)的算子矩阵可以表示为

Qφ=ΦQBΦ-1

(9)

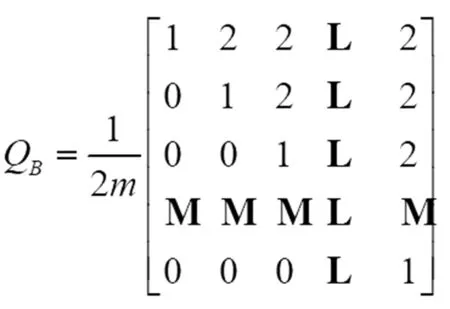
(10)

若Φ(t)为正交矩阵,那么QΦ=ΦQBΦT

对任意函数y(x,t)∈L2(R)可展开为小波积形式

=H(x)TCH(t)

(11)

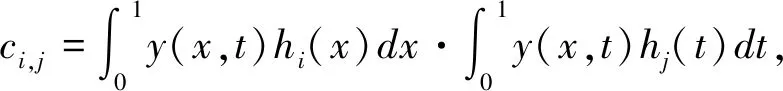
Y=HTCH

(12)

这里Y为y(x,t)的离散形式,即有

其中,hi,j=hi((j+1/2)/m),y(x,t)的系数矩阵为

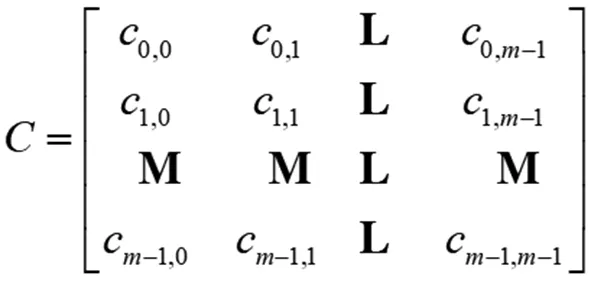
并可由公式C=(HT)-1·Y·H-1求得,由Haar小波性质可知H为正交矩阵,因此有

C=H·Y·HT

(13)

考虑如下分数阶方程:

(14)

其中d(x,t),g(x,t)∈C(D)为已知函数,u(x,t)∈L2(D),这里D=[0,1]×[0,1]。由于u(x,t)为平方可积函数,可设

=HT(x)CH(t)

(15)

于是由(8)～(10)式可得

=HT(x)CQH-αH(t)

(16)

=(QH-βH(x))TCH(t)

(17)

将(16),(17)代入到(14)得

HT(x)CQH-αH(t)

=-d(x,t)·(QH-βH(x))TCH(t)+g(x,t)

(18)

HTCQH-αH=-[d(xi,tj)]m×m∘(QH-βH)TCH

+[g(xi,tj)]m×m

(19)

其中∘表示阿达马乘积[13],它满足如下形式:

如果A=[aij]m×m,B=[bij]m×m,则A、B的阿达马乘积A∘B=[aijbij]m×m

方程(19)可通过MATLAB解出矩阵C,进而方程可解。

此方法的收敛性已在文献[12]中证明，由于篇幅限制不再赘述。

3 数值算例

考虑如下时间-空间分数阶偏微分方程

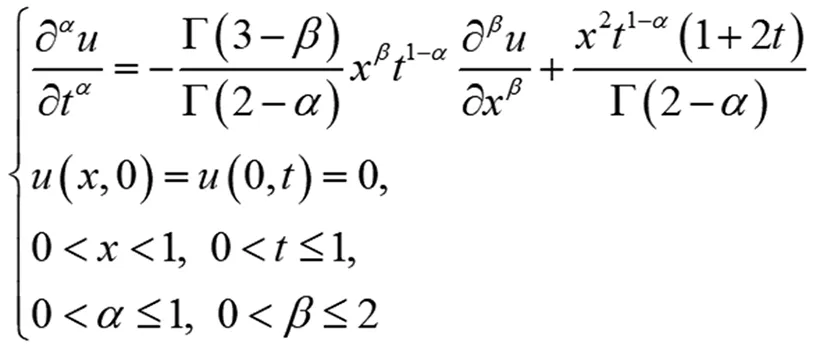
(20)

结合上述方法利用MATLAB软件进行数值计算,取不同的α,β得到表1～3。

表1 α=0.2,β=1.2时数值解与精确解的误差

表2 α=0.6,β=0.8时数值解与精确解的误差

表3 α=0.6,β=1.2时数值解与精确解的误差

对于α=0.2,β=1.2,取m=8,m=16,m=32时,用MATLAB求解精确解和数值解之间的绝对误差与比较如图1～4。

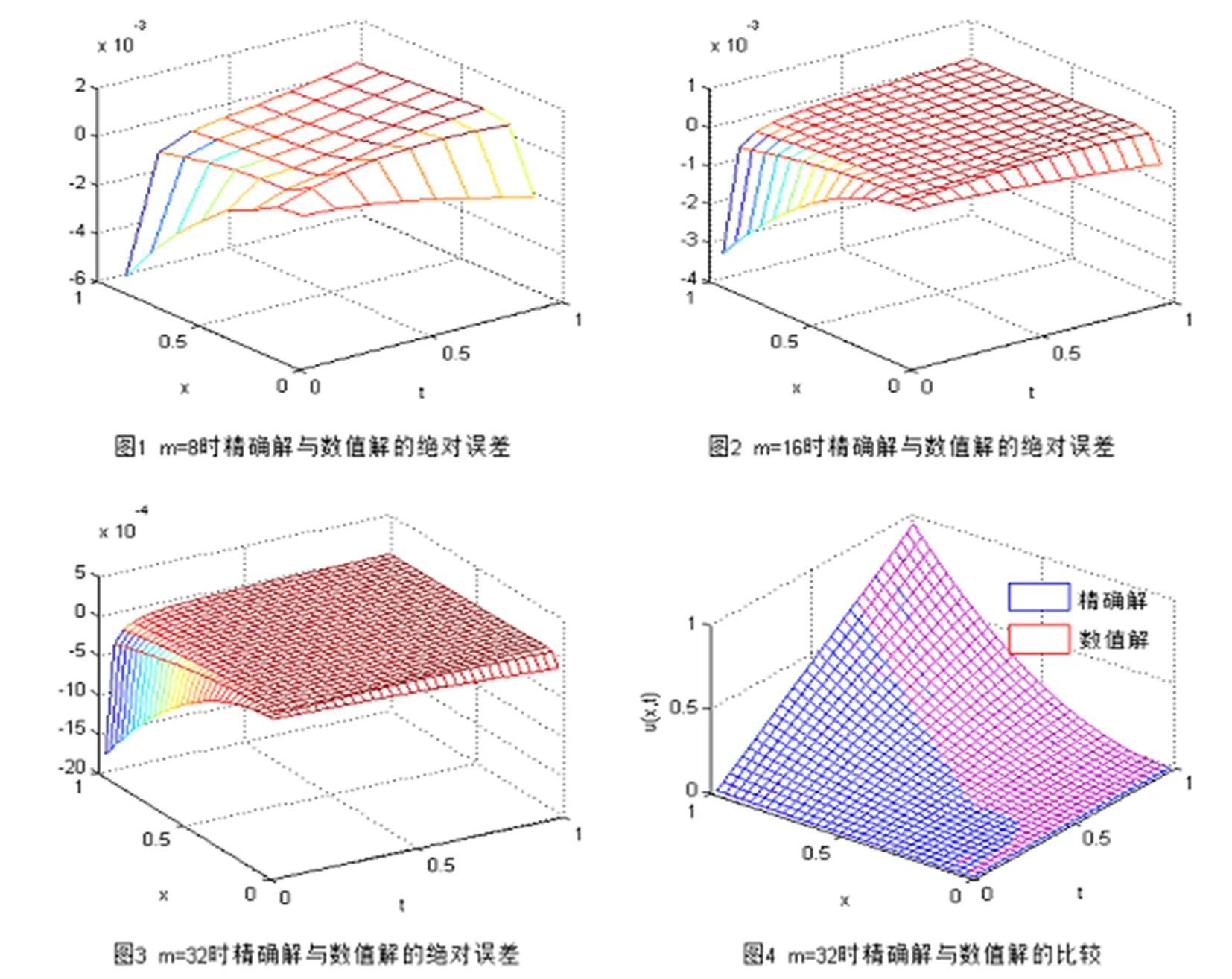
计算结果表明,Haar小波可用来求解系数为时间-空间变量的分数阶偏微分方程。表格通过α,β对比不同,取值时,精确解与数值解之间的L2,L∞验证了方法的可行性和有效性。从图中可以更清晰的看到,随着m的增大,精确解和数值解的绝对误差逐渐变小,逼近度逐渐变高。同时本文方法要比直接采用差分格式更简便,计算量更小。

4 结论

本文运用Haar小波与算子矩阵有效结合的思想,将原问题转化为求解矩阵代数方程的问题,更加有利于计算机求解。在处理时间-空间变系数时,引入阿达马乘积的概念,提高了运算的精度。同时由于Haar小波矩阵本身具有稀疏性和正交性,所以本文提出的数值方法更能简单有效地解决一类分数阶偏微分方程的初值问题。