线性分数自排斥扩散的收敛性

李洪伟， 葛 勇， 闫理坦

（东华大学 理学院，上海 201620）

1991年，Durrett 和Rogers[1]首先研究了一种用于模拟聚合物形状变化的数学模型。他们考察了下列随机微分方程解在满足一定条件时的渐近行为

其中B 是d-维标准布朗运动，Φ 是Lipschitz 连续函数。在1995年，Cranston 和Lejan[2]在此基础上提出了自吸引扩散模型，并重点研究了下面的两种一维情况：

（1）线性自交互型：Φ 为一个线性齐次函数Φ（x）＝ax

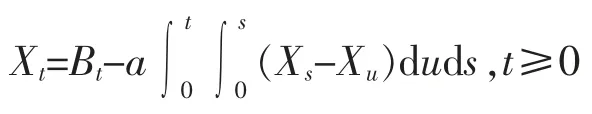
其中a＞0。

（2）常自交互型：Φ（x）＝σsign

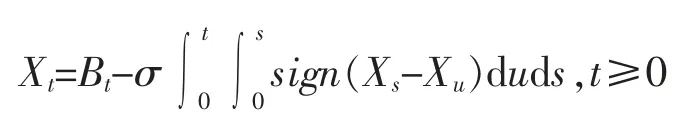
其中σ＞0。他们证明了上述两种情况下，方程的解Xt是几乎必然收敛的。对于方程（1），如果对函数Φ 不加任何限制，那么它就是一个自交互扩散过程；特别地，如果对任意的x∈Rd，有x·Φ（x）≥0，称方程（1）的解是自排斥的；相反地，如果对任意的x∈Rd，有x·Φ（x）≤0，称方程（1）的解是自吸引的。如果想更多地了解自交互过程的相关研究，可以参见文献[3-7]。

另一方面，利用分数布朗运动的随机性质，可以建立一个路径积分，用于模拟聚合物生成时的形状变化。因此，在文献[8－9]的基础上，闫理坦等在文献[10]中考察了如下方程

其中BH是一个Hurst 指数为H∈（0，1）的d-维标准分数布朗运动。不难证明上述方程具有唯一的强解，同时他们重点讨论了如下方程

他们证明了当a<0 且H>1/2 时该方程的解（称为分数自吸引扩散）是均方收敛的，同时也是几乎必然收敛的，并给出了该方程在离散形式下的收敛性定理。甘姚红与闫理坦研究了a，v 在a>0 时的最小二乘估计[12]。笔者主要研究a>0 时方程（3）解的收敛性。

1 预备知识

在这部分中，简要介绍分数布朗运动的概念、基本性质以及相关的随机积分，除特别声明外，以下通篇假设H>1/2，且是一个定义在（Ω，FH，P）上的一维分数布朗运动，其Hurst 指数为H，其中FH是由BH生成的σ 代数。Hurst 指数为H 的分数布朗运动是一个均值为零的高斯过程，其协方差函数为

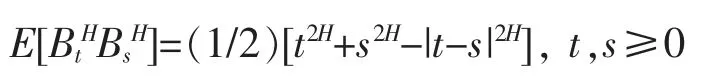
当H＝1/2 时，BH为标准布朗运动。由于分数布朗运动在H≠1/2 时， 它既不是半鞅也不是马尔科夫过程，因此，很多随机分析中的方法并不适用，但作为高斯过程，可以构造BH的基于随机变分法的随机分析。

假设ε 是由示性函数1[0，t]，t≥0 张成的线性空间，而是ε 的基于如下内积的完备化

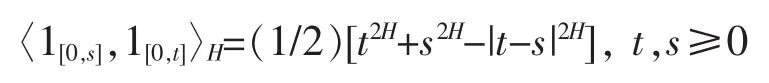
考虑如下定义在ε 上的线性映射

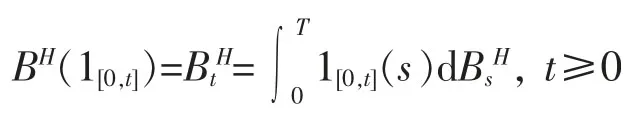
可以证明，这个映射在ε 上是线性的并且它也是一个ε 到BH生成的高斯空间的一个等距，这个等距可以被扩张到上。称这个等距映射为关于BH的Wiener 积分，记成

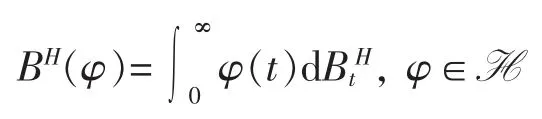
2 主要结果与证明

假设C 是一个正常数，其值可能依赖于H、a、v，并且它们的值在不同位置可能不同。显然方程（3）的解可以表示为

其中，

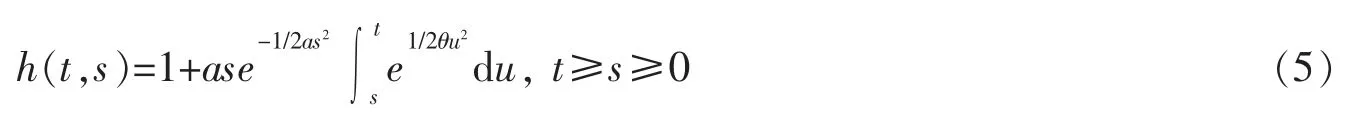
当t趋于无穷大时，显然方程（4）是发散的，但由洛必达法则，下式成立

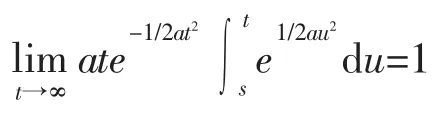
于是，有

定理1设是方程（3）的解。则当t趋于无穷大时为L2（Ω）收敛，且收敛于如下的随机变量

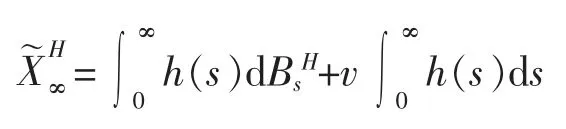
证明为了叙述简单，记，利用洛必达法则，对于任意的s＞0，下式均成立

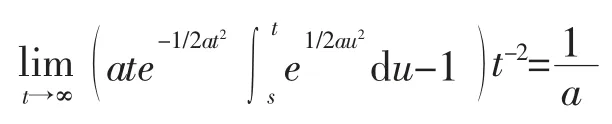
所以存在一个正常数C，使得对于任意的0＜s≤t 均有

注意对所有t＞0，

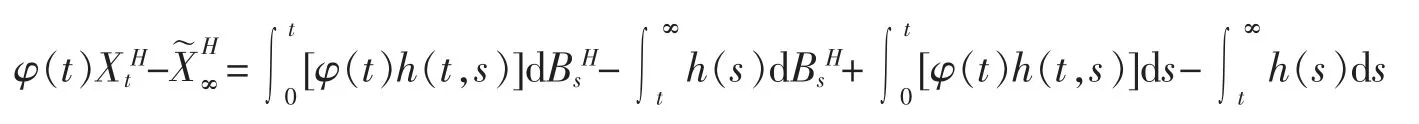
所以，有

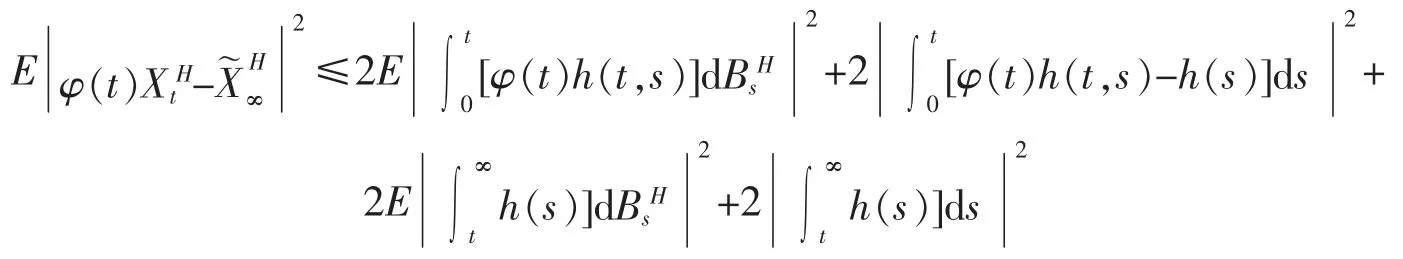
当t趋于无穷大时，显然上式中最后一项趋于0，而倒数第二项满足

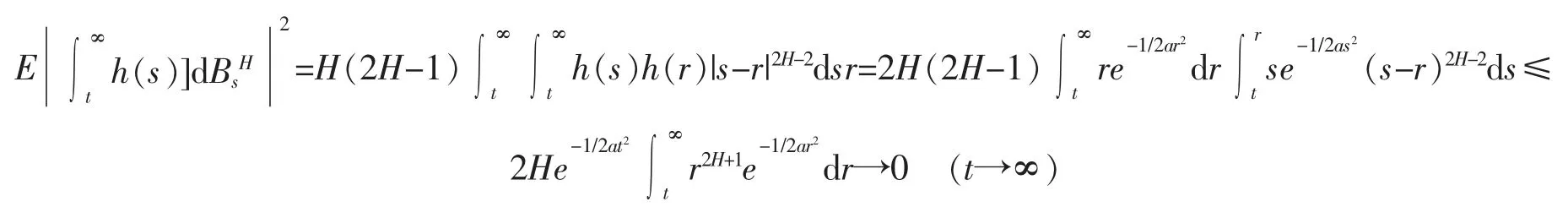
现在证明前两项当t 趋向于无穷大时也趋向于0。由式（7），得到如下不等式

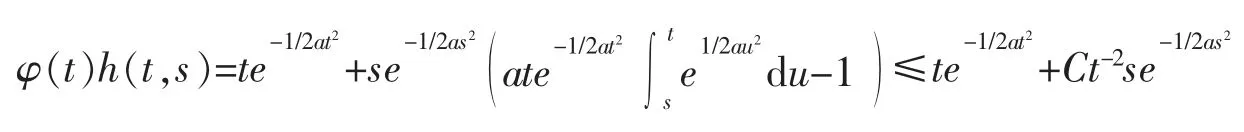
由此可得

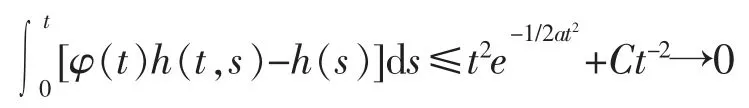
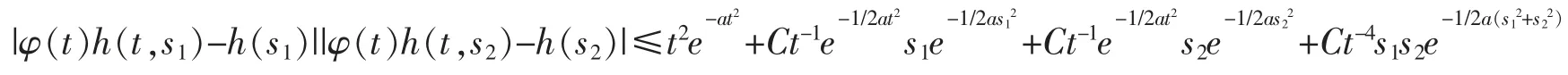
所以，有

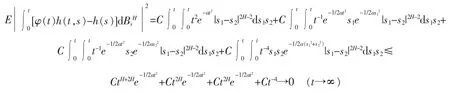
证毕。

定理2当t 趋向于无穷大时几乎必然收敛于

证明不失一般性，这里假设v＝0，由方程（3），有

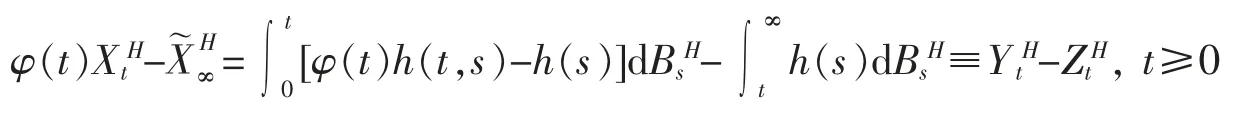
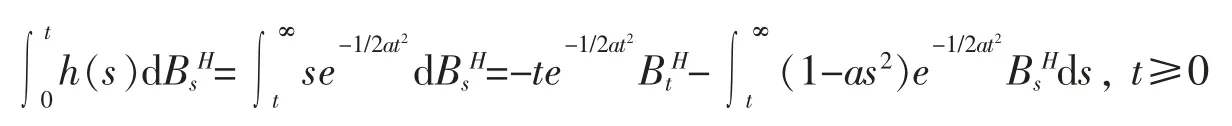
由事实

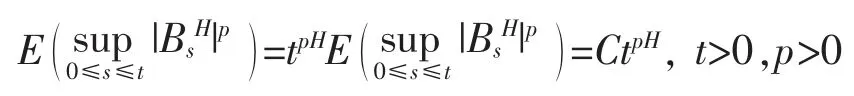
及

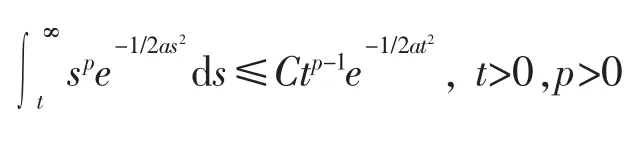
得到以下估计

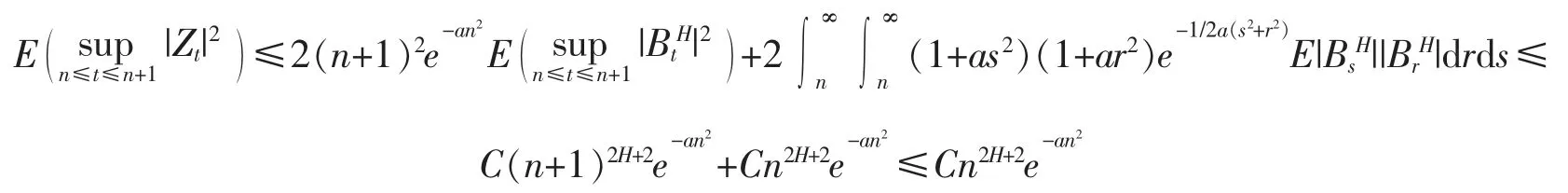
对任意的n≥1 均成立，所以

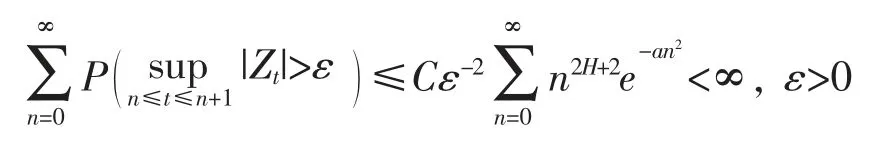
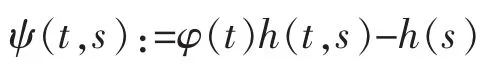
这里t≥s＞0，则有

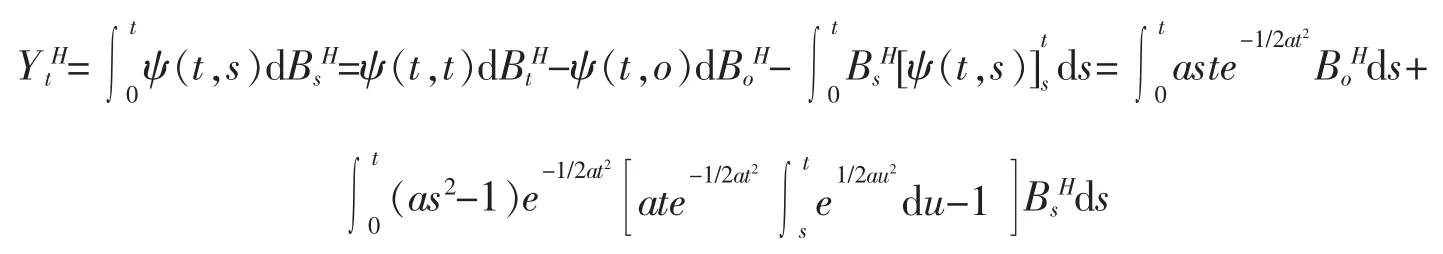
对于上述第一项积分，有

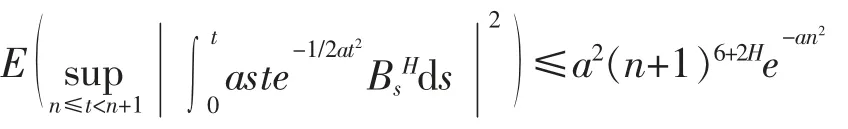
对于方程（7）中的第二项积分，也有

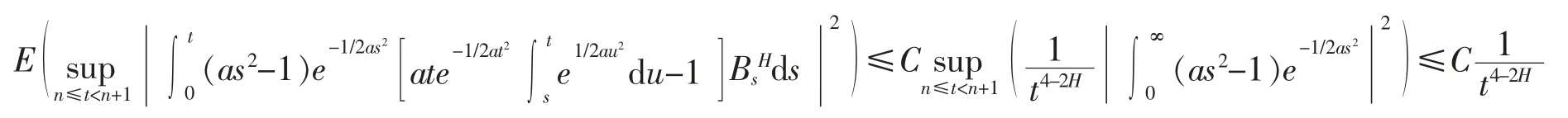
于是，结合Borel-Cantelli 引理，同样证明了当t 趋向于无穷大时几乎必然收敛于0。证毕。