A note on weak 2-local isometries on differentiable function spaces

LI Lei

（School of Mathematical Sciences，Nankai University，Tianjin 300071，China）

Abstract： Let C1[0，1]be the Banach algebra of complex valued continuously differentiable functions with the norm ||f||L＝max{|f（x）|+|f ′（x）| : x∈[0，1]} or ||f||s＝||f||∞+||f ′||∞.The weak-2-local isometries between C1[0，1]are linear maps.

Key words： weak-2-local isometries；differentiable functions；spherical Kowalski-Słodkowski theorem

1 Introduction

Recall that a map Φ between the algebra A is a 2-local automorphism （respectively，2-local derivation） if for every a，b∈A there exists an automorphism （respectively，derivation） Φa，b:A→A，depending on a and b，such that Φa，b（a）＝Φ（a） and Φa，b（b）＝Φ（b）.P.Šmerl[1]proved that every 2-local automorphism of the Banach algebra B（H） of all bounded linear operators on an infinite dimensional separable Hilbert space H is an automorphism，and a similar assertion was stated concerning the 2-local derivations.Later，Sh.Ayupov and K.Kudaybergenov[2]introduced a new technique to generalize the above results for arbitrary Hilbert spaces.Moreover，K.K.Kudaybergenov，T.Oikhberg，A.M.Peralta，B.Russo[3]studied the 2-local triple derivations on von Neumann algebras.

Motivated by these results，Molnár[4]extended the notion of 2-locality to isometries as follows.Given a Banach space X，a map Φ:X→X is said to be a 2-local isometry if for every x，y∈X there is a surjective linear isometry Φx，y:X→X，which depends on x and y，such that Φx，y（x）＝Φ（x） and Φx，y（y）＝Φ（y） （neither linearity nor surjectivity on Φ is assumed）.Molnár[4]showed that every 2-local isometry of B（H） is a surjective linear isometry.

Furthermore，Molnár[4]strated the study of 2-locality for function algebras.In this direction，Györy[5]showed that if X is a first countable σ-compact Hausdorff space then every 2-local isometry of C0（X） is a surjective linear isometry.Later，H.Al-Halees and R.J.Fleming[6]studied the 2-local isometries on vector-valued continuous function spaces.Hatori，et al[7]considered 2-local isometries on uniform algebras including certain algebras of holomorphic functions of one and two complex variables.A.Jiménez-Vargas and M.Villegas-Vallecillos[8]gave a complete description of all 2-local isometries on scalar-valued Lipschitz function spaces Lip（X） when X is bounded and the isometry group of Lip（X） is canonical.A.Jiménez-Vargas，L.Li，A.M.Peralta，L.Wang，Y.-S.Wang[9]gave a description of the 2-local （standard） isometries on vector-valued Lipschitz function spaces Lip（X，E） under some conditions on a compact metric space X and on a Banach space E；and then proved that these mappings are both linear and surjective.

More generally，Niazi and Peralta[10-11]gave the general definition of weak 2-local maps.

Definition 1Let S be a subset of the space B（X，Y） of all bounded linear maps between Banach spaces X and Y.A（not-necessarily linear nor continuous） mapping Δ:X→Y is a weak-2-local S-map if for each x，y∈X and φ∈Y*，there exists Tx，y，φin S，depending on x，y，and φ，satisfying

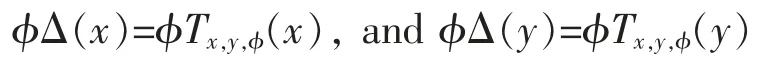
In the case of S＝Der（A），the subspace of all derivations on a Banach algebra A，Niazi and Peralta[10]proved that every weak 2-local derivation on a finite dimensional C*-algebra is a linear derivation.Sh.Ayupov，K.Kudaybergenov[12]showed that every 2-local derivation on a von Neumann algebra is a derivation.For more recently results about 2-local derivations，one can see[13].When S＝Iso（X，Y），the space of all surjective linear isometries from X onto Y，Li，Peralta，L.Wang and Y.-S.Wang[14]studied the weak-2-local isometies on uniform algebras and Lipschitz function algebras.

In this note，we will establish the weak-2-local isometries on the algebra of complex-valued differentiable functions.

2 Main results

Suppose that （C1[0，1]，||·||L） is the Banach algebra of all complex-valued differentiable functions on [0，1]，where

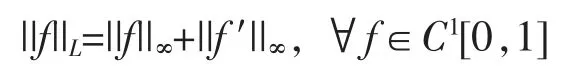
In order to study the weak-2-local isometry on （C1[0，1]，||·||L），we need the spherical variant of the Kowalski-Słodkowski theorem as follows.

Proposition 1[14]Let A be a unital complex Banach algebra，and let Δ:A→C be a mapping satisfying the following properties：

（a）Δ is 1-homogeneous；

（b）Δ（x）-Δ（y）∈Tσ（x-y），for every x，y∈A.

Then Δ is linear，and there exists λ0∈T such that λ0Δ is multiplicative.

For any surjective linear isometry T:（C1[0，1]，||·||L）→（C1[0，1]，||·||L），it follows from [15，Theorem 4.1]that there exist λ∈T and a surjective mapping σ:[0，1]→[0，1]with σ＝id or σ＝1-id such that

Theorem 1Every weak-2-local isometry Δ from （C1[0，1]，||·||L） to itself is a linear map.

ProofLet Δ:C1[0，1]→C1[0，1]be a weak-2-local isometry with respect to the norm ||·||L.It is known that Δ is 1-homogeneous （i.e.，Δ（αf）＝αΔ（f），for all α∈C and all f∈C1[0，1]），and Δ（0）＝0 （compare [16，Lemma 2.1]）.We fix now an element s∈[0，1]，and we consider the mapping Δs:＝δs◦Δ:C1[0，1]→C.By the hypothesis and [15，Theorem 4.1]，given f，g∈C1[0，1]，there exist τf，g，s∈T and a surjective mapping φf，g，s:[0，1]→[0，1]such that

and

This implies that

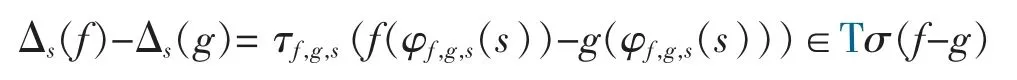
Since （C1[0，1]，||·||L） is a unital complex Banach algebra，we are thus in conditions to apply Proposition 1 to conclude that Δsis a linear map.The linearity of Δ follows from the arbitrariness of s.□

It is well-known that （C（n）[0，1]，||·||S），the scalar-valued n-times continuously differentiable function space，is also a Banach algebra，where

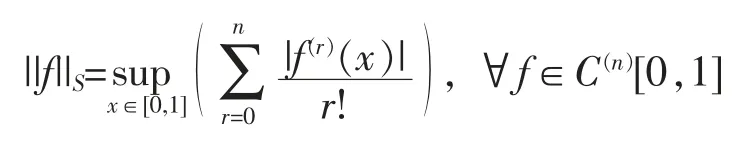
It follows from [17，Theorem 2.5]that every surjective linear isometry T:（C（n）[0，1]，||·||S）→（C（n）[0，1]，||·||S）can be written as the form （1）.So we can get the following theorem by a similar argument.

Theorem 2Every weak-2-local isometry Δ from （C（n）[0，1]，||·||S） to itself is a linear map.