剪切理论与经典理论的对称角铺设方板弯曲解析研究

张承宗

(空军某军事代表局，北京 100071)

0 引言

复合材料层合板壳结构元件具有轻质高强、可设计性好等诸多优点，在现代工业中获得了广泛应用。复合材料的各向异性为板壳力学研究增加了新的内涵[1]。人们早在1947年[2]就开始针对各向异性板力学问题进行系统研究，但因为数学理论的局限，对正交异性问题研究开展的较多，而对各向异性研究成果相对有限。针对板壳剪切效应，相继提出了Ressner一阶剪切理论(First-Order Deformation Theory， FSDT)[3]、Reddy简化高阶剪切理论(Reddy Simplified High Order Shear Deformation Theory， RSDT)[4]等。从数学上看，经典板理论(Classical Laminated Plate Theory， CLT) 是一个未知位移函数的4次偏微分方程边值问题，Ressner一阶剪切理论是3个未知位移函数的6次偏微分方程边值问题，Reddy简化高阶剪切理论是3个未知位移函数的8次偏微分方程边值问题，数学解析求解难度在提升。而对于复合材料对称角铺设层合板结构，各向异性还带来了奇次交叉刚度系数,不论是解析法求解，还是数值法求解均不容易。近年来，数学物理方法获得进步[5-10]，陆续发展了复数级数方法，基于经典理论[5]、Ressner一阶剪切理论[8]、Reddy简化高阶剪切理论[12]各向异性板弯曲力学问题一般解析解，使解析研究各向异性板壳结构力学响应问题成为了可能。应用复数级数方法求解了基于Reddy简化高阶剪切理论各向异性板弯曲力学问题，进一步研究发现[12],解的多项式补充解需进一步简化。由此，在此基础上，本文对Reddy简化高阶剪切理论的各向异性板弯曲问题重新进行了解析求解，得到了简化后的该问题一般解析解。

不同剪切理论与经典理论在各向异性情况下的适用范围是工程设计和理论分析所关心的。本文应用解析解方法分别采用Ressner一阶剪切理论、Reddy高阶简化剪切理论和经典理论板弯曲解析解，计算研究不同铺设角、铺设层数、板厚条件下四边固支对称角铺设层合板弯曲问题，通过分析比较其挠度、弯矩、扭矩变化情况，研究对于四边固支层合板弯曲问题的各理论适用范围和力学响应变化规律。计算发现，四边固支对称角铺设层合方板在h/a≤0.02时，经典理论和这两种剪切理论的板中心挠度、弯矩、扭矩计算值相差不大；h/a>0.02时，两种剪切理论和经典理论的板中心挠度计算值开始出现差距。对于四边固支层合方板，Ressner一阶剪切理论和Reddy简化高阶剪切理论的板中心挠度计算值相差不大。对于四边固支层合板，两种剪切理论的板中心弯矩和扭矩亦相差不大。为反映横向剪切影响程度，引入了横向剪切效应参数。数值算例表明，对于四边固支对称角铺设层合板弯曲问题，横向剪切效应与弯扭耦合效应存在交联。文中给出一批数值算例，可供有限元等数值计算程序校核参考。

1 基本理论

对于矩形板弯曲问题，引入以下无量纲量

其中,a、b、h分别为矩形板的长、宽、厚,q为横向载荷,(x,y,z)为直角坐标系坐标，z为平板中面法向坐标，x、y分别为长、宽方向坐标。

1.1 Reddy简化高阶剪切理论

基于Reddy简化高阶剪切理论的对称角铺设层合板在弯曲变形分析时的位移分量为

(1)

式中,w(x,y)为挠度，u(x,y)、v(x,y)分别为x、y方向位移，φx(x,y)、φy(x,y)分别为板广义位移参量。

该横向弯曲问题的平衡方程可写为如下形式

(2)

其中，微分算子L33,L34,…,L55见下文。

其中,广义刚度为

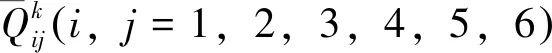
设

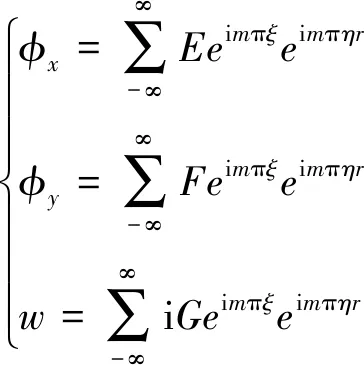
(3)

式中，i为虚数单位，m为整数(m≠0，实际计算中m是有限的，设最大项数为M)，r为复数特征根。E、F、G为复数常数。根据文献[12],可得实数形式的一般解析解

t1+t2(ξ-0.5)+t3(η-0.5)+t4(ξ-0.5)2+t5(η-0.5)2+t6(ξ-0.5)(η-0.5)+t7(ξ-0.5)3+

t8(ξ-0.5)2(η-0.5)+t9(ξ-0.5)(η-0.5)2+t10(η-0.5)3+t23(ξ-0.5)4+t24(ξ-0.5)3(η-0.5)+

t25(ξ-0.5)2(η-0.5)2+t26(ξ-0.5)(η-0.5)3+t27(η-0.5)4+

(4)

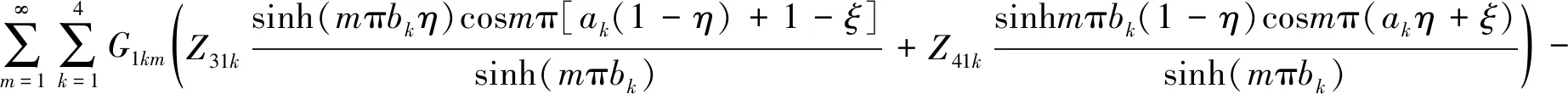
t11+t12(ξ-0.5)+t13(η-0.5)+t14(ξ-0.5)2+t15(η-0.5)2+t16(ξ-0.5)(η-0.5)+

t28(ξ-0.5)3+t29(ξ-0.5)2(η-0.5)+t30(ξ-0.5)(η-0.5)2+t31(η-0.5)3+

(5)

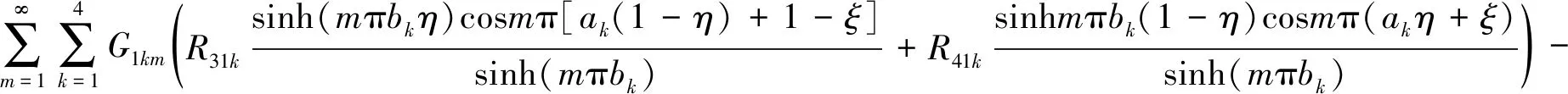
t17+t18(ξ-0.5)+t19(η-0.5)+t20(ξ-0.5)2+t21(η-0.5)2+t22(ξ-0.5)(η-0.5)+

t32(ξ-0.5)3+t33(ξ-0.5)2(η-0.5)+t34(ξ-0.5)(η-0.5)2+t35(η-0.5)3+

(6)

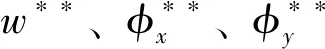
wp=t1+t2(ξ-0.5)+t3(η-0.5)+t4(ξ-0.5)2+

t5(η-0.5)2+t6(ξ-0.5)(η-0.5)+t7(ξ-

0.5)3+t8(ξ-0.5)2(η-0.5)+t9(ξ-0.5)·

(η-0.5)2+t10(η-0.5)3+t23(ξ-0.5)(η-

0.5)3+t24(ξ-0.5)3(η-0.5) +t25(ξ-

0.5)2(η-0.5)2

0.5)2+t15(η-0.5)2+t16(ξ-0.5)(η-0.5)+

t26(ξ-0.5)3+t27(ξ-0.5)2(η-0.5)+

t28(ξ-0.5)(η-0.5)2+t29(η-0.5)3

0.5)2+t21(η-0.5)2+t22(ξ-0.5)(η-

0.5)+t30(ξ-0.5)3+t31(ξ-0.5)2(η-

0.5)+t32(ξ-0.5)(η-0.5)2+t33(η-0.5)3

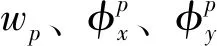
内力矩计算公式如下

[Mx,My,Mxy]T=[Di,j]{e2}+[Hi,j]{e4}
(i,j=1,2,6)

(7)

其中,刚度Dij、Hij定义见文献[12-13]。式中

1.2 Ressner一阶剪切理论

根据文献[3,8]，基于Ressner一阶剪切理论的对称角铺设层合板在弯曲变形分析时的位移分量为

(8)

式中，w(x,y)为挠度，φx(x,y)和φy(x,y)分别为板广义位移参量。Ressner一阶剪切理论的对称角铺设层合板横向弯曲问题控制偏微分方程组及其一般解析解见文献[8]。

一阶剪切理论板弯曲内力计算公式如下

[Mx,My,Mxy]T=[Di,j]{e2} (i,j=1,2,6)

(9)

其中，{e2}与公式(7)中定义相同。

本文计算沿用文献[8]中根据剪切余能相等原理推导出修正剪切刚度系数的做法，修正剪切刚度系数A55、A45、A44具体形式见文献[8,13]。

1.3 经典理论

经典理论各向异性板弯曲控制偏微分方程如下

(10)

采用复数级数法[5]可求解对称角铺设层合矩形板横向弯曲问题，具体解形式见文献[5]。

内力矩计算公式为

(11)

1.4 边界条件与角点条件

Reddy简化高阶剪切理论四边固支矩形板边界条件为

(12)

Reddy简化高阶剪切理论四边固支矩形板角点条件为

(13)

一阶剪切理论的四边固支矩形板边界条件为

(14)

一阶剪切理论的四边固支矩形板角点条件为

ξ=0,1η=0,1φx=0φy=0w=0

(15)

经典理论四边固支矩形板边界条件为

(16)

经典理论四边固支矩形板角点条件为

(17)

2 计算研究

下面采用解析解方法(经典理论解见文献[5]，Ressner一阶剪切理论解见文献[8]，Reddy简化高阶剪切理论解见文献[12])计算对称角铺设四边固支方形板在均布载荷q作用下的弯曲，评估有关理论解析解适用范围，并研究横向弯曲力学响应情况。本文设定板结构参数为a=b=1m(选定方板进行计算研究)，载荷参数为q=104N/m2，材料力学参数为:E1=276GPa，E2=31.05GPa，G12=G13=10.35GPa，G23=12.42GPa，ν12=ν13=0.25，ν23=0.28。

该弯曲问题中挠度中心对称；φx、φy反中心对称(对于剪切理论计算而言)，据此可降低计算量。挠度单位为m，弯矩、扭矩单位为N·m。铺设角θ的单位为(°)，铺设方式确定为对称角铺设，如[θ,-θ,θ]T，本文以下所提层合板均为对称角铺设层合板。铺设层数为N(注意斜体为变量-铺设层数)，计算假定层合板各层厚度一致，板厚h确定后，铺设层数N可以调整。

2.1 验证计算

为了检验本文式(4)～式(6)的收敛性和稳定性，针对11层[30°/-30°/30°/-30°/30°/-30°/30°/-30°/30°/-30°/30°]铺设四边固支正方形板(h=0.1m)，在均布载荷作用下的横向弯曲进行计算，改变M比较相应板中心挠度和弯矩，结果见表1～表2。

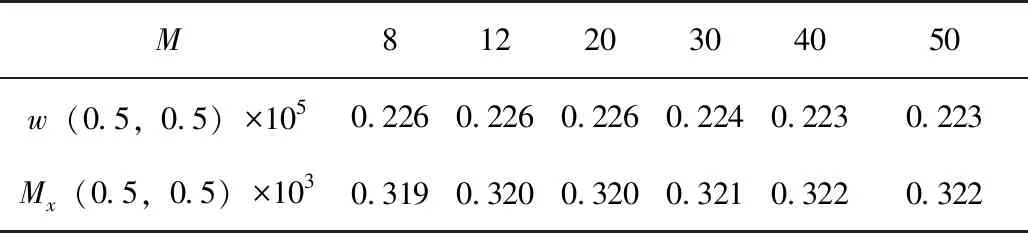
表1 M对板中心挠度、弯矩计算值影响

表1表明，当M增大时，本文解数值保持稳定。计算中发现，对于不同的材料、边界条件及铺层方式 ，也存在相同的趋势。

为检查本文解的边界条件符合情况，针对单层铺设角为30°的正方形板(h=0.1m)进行计算(M=60)。板挠度w、广义位移φx和φy计算结果见表2～表4。

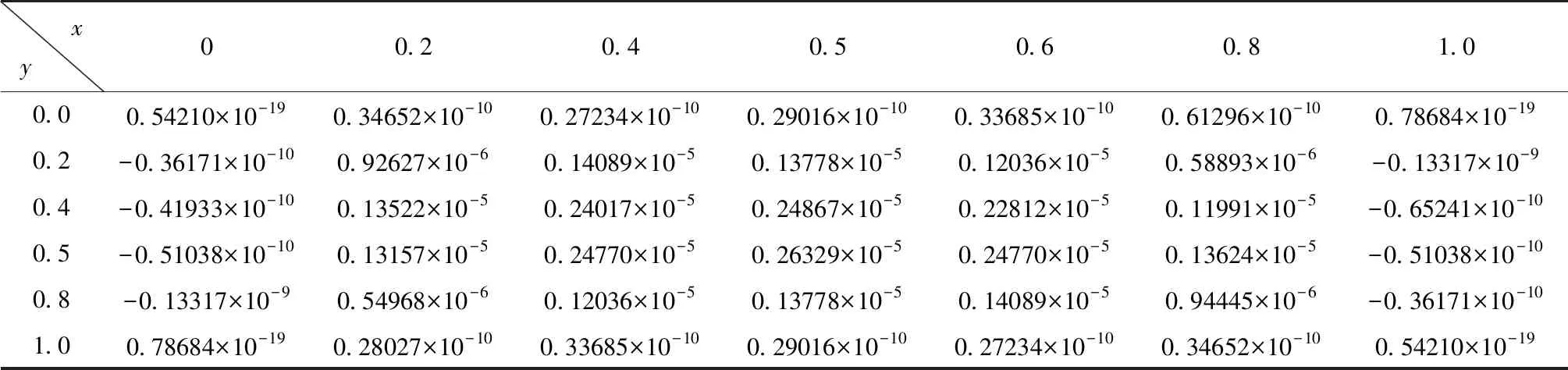
表2 [30°] CCCC层合板挠度w(x,y)分布

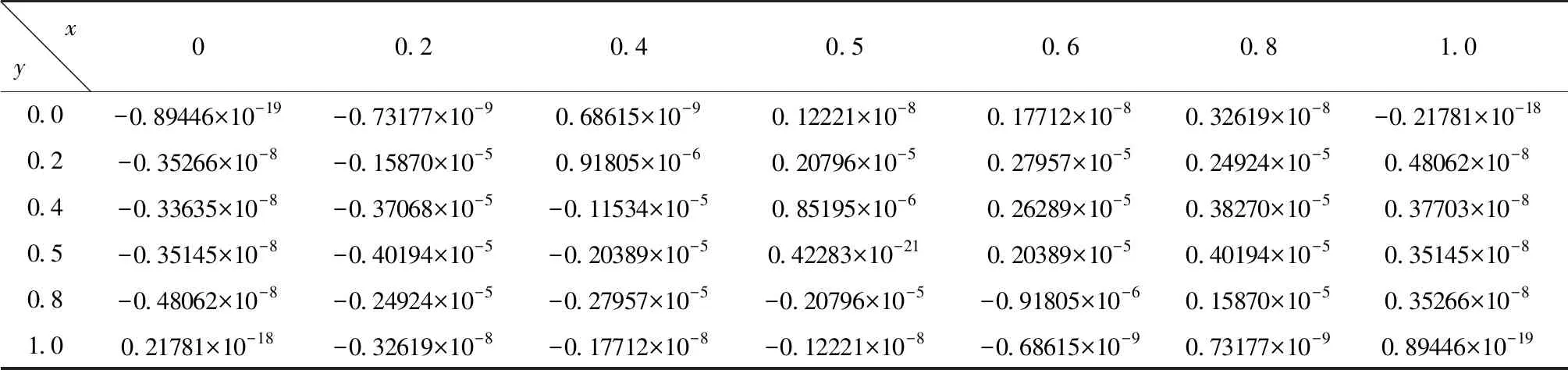
表3 [30°] CCCC层合板φx分布

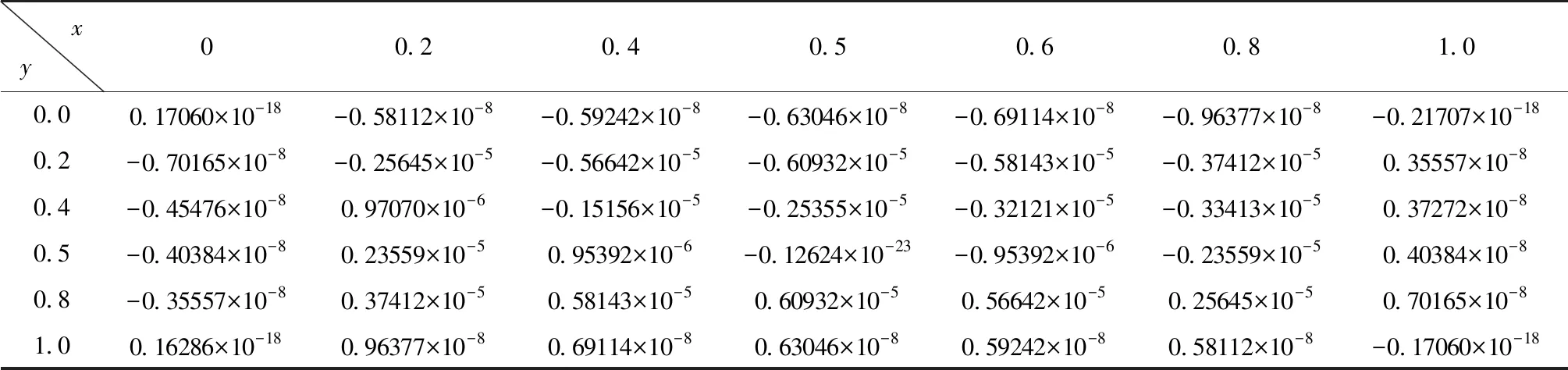
表4 [30°] CCCC层合板φy分布

由表2～表4可发现,本文解对位移边界条件符合程度较好。

为检验本文解与已有解符合情况，固定a=b=1m，改变h，结合不同a/h，针对具有CCCC边界条件[45°/-45°/45°]层合方板，计算板中心挠度和弯矩值，并将Reddy简化理论解与经典理论CLT[9]、修正剪切刚度的FSDT[12]进行对比(M取40)。计算结果见表5～表6。

表5 [45°/-45°/45°] CCCC层合板中心挠度RSDT解与CLT、FSDT解比较

表6 [45°/-45°/45°]T CCCC层合板中心弯矩Mx(0.5,0.5) RSDT解与CLT、FSDT解比较

由表5～表6可看出：当a/h增大到一定值时，RSDT解数值已经接近CLT、FSDT解数值；当a/h降低到一定值时，RSDT解与CLT解的挠度值、弯矩逐渐出现差距。在目前设定的边界条件、铺设方式、结构尺寸和板中心位置，RSDT解与FSDT解挠度值、弯矩比较接近，FSDT解挠度值一般要略大于RSDT解挠度值。以上的计算结果从不同的方面验证了本文解的正确性和收敛性。

2.2 挠度、弯矩和扭矩对比计算结果

对不同板厚h、不同铺层N和不同铺设角θ的对称角铺设层合板中心挠度、弯矩、扭矩进行计算，具体结果见表7～表10。对3种级数形式一般解析解计算时均选取M=60(项)。

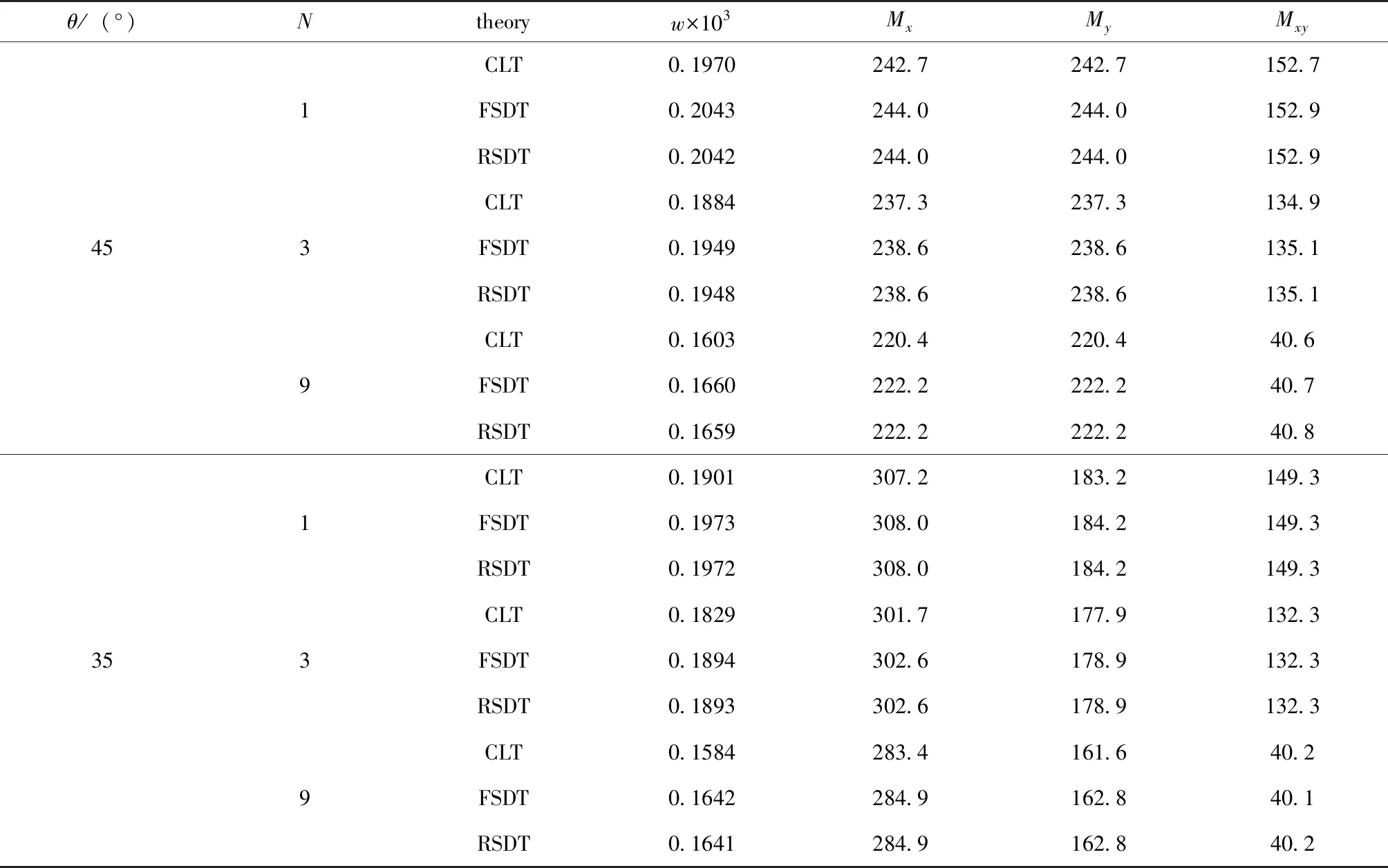
表7 四边固支层合板中心挠度、弯矩和扭矩的RSDT与FSDT、CLT计算值对比(h=0.02m,a=b=1m)

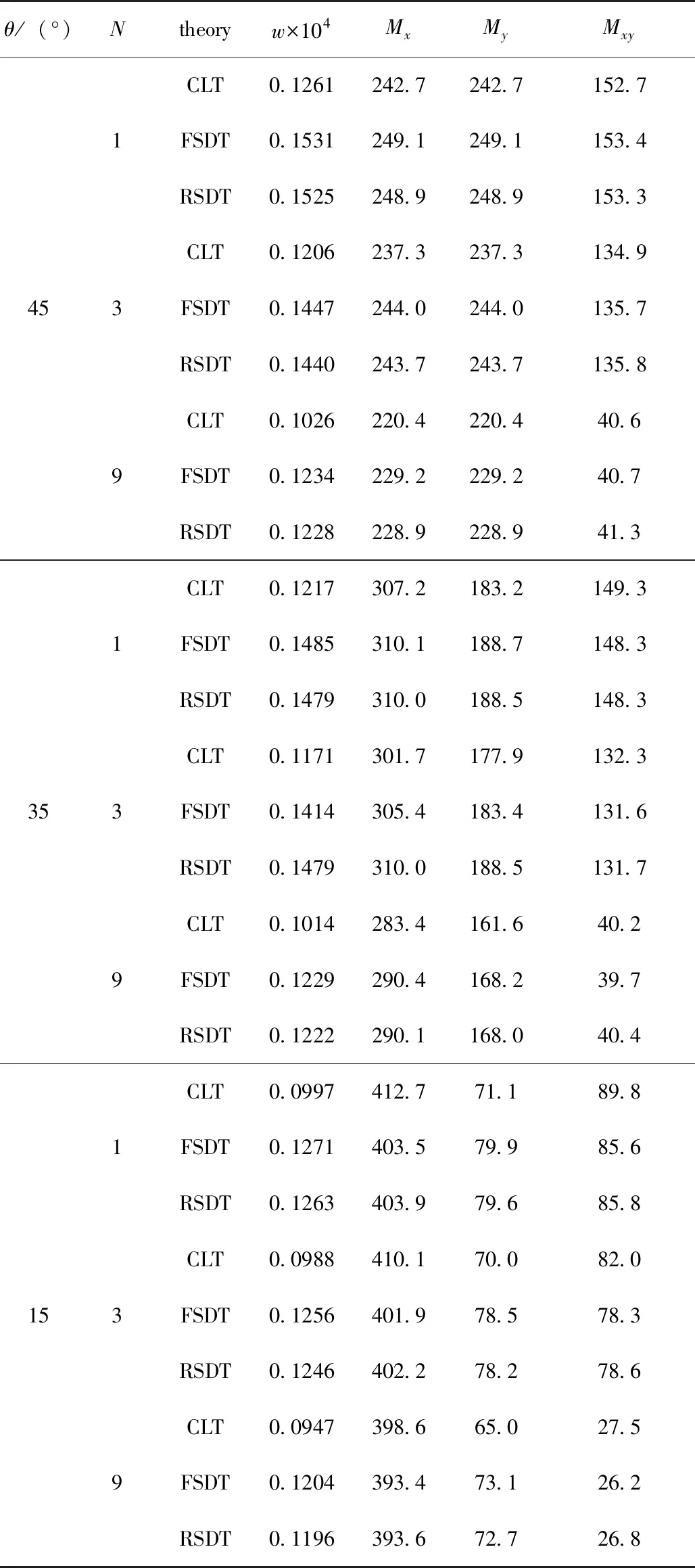
表8 四边固支层合板中心挠度、弯矩和扭矩的RSDT与FSDT、CLT计算值对比(h=0.05m,a=b=1m)

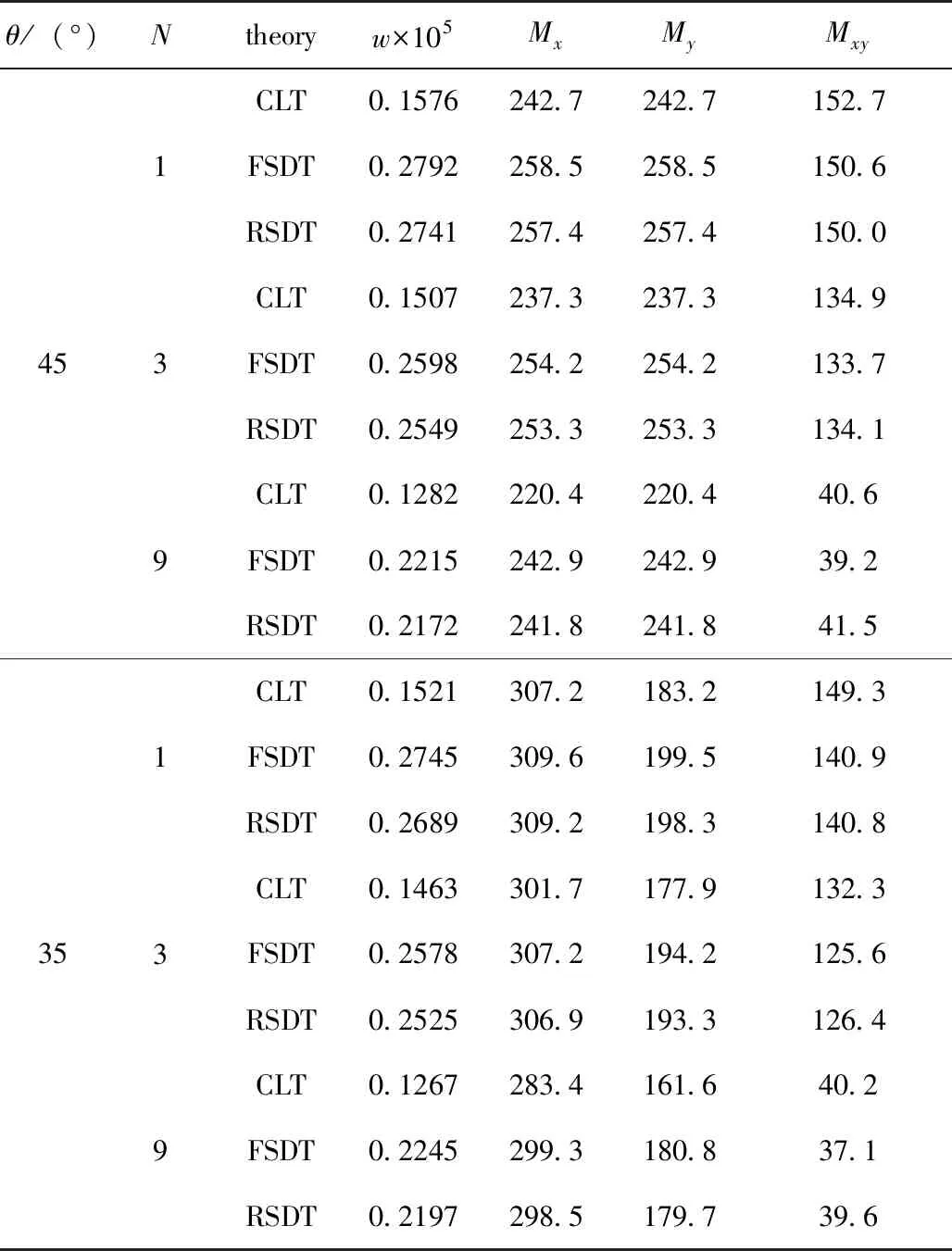
表9 四边固支层合板中心挠度、弯矩和扭矩的RSDT与FSDT、CLT计算值对比(h=0.1m,a=b=1m)

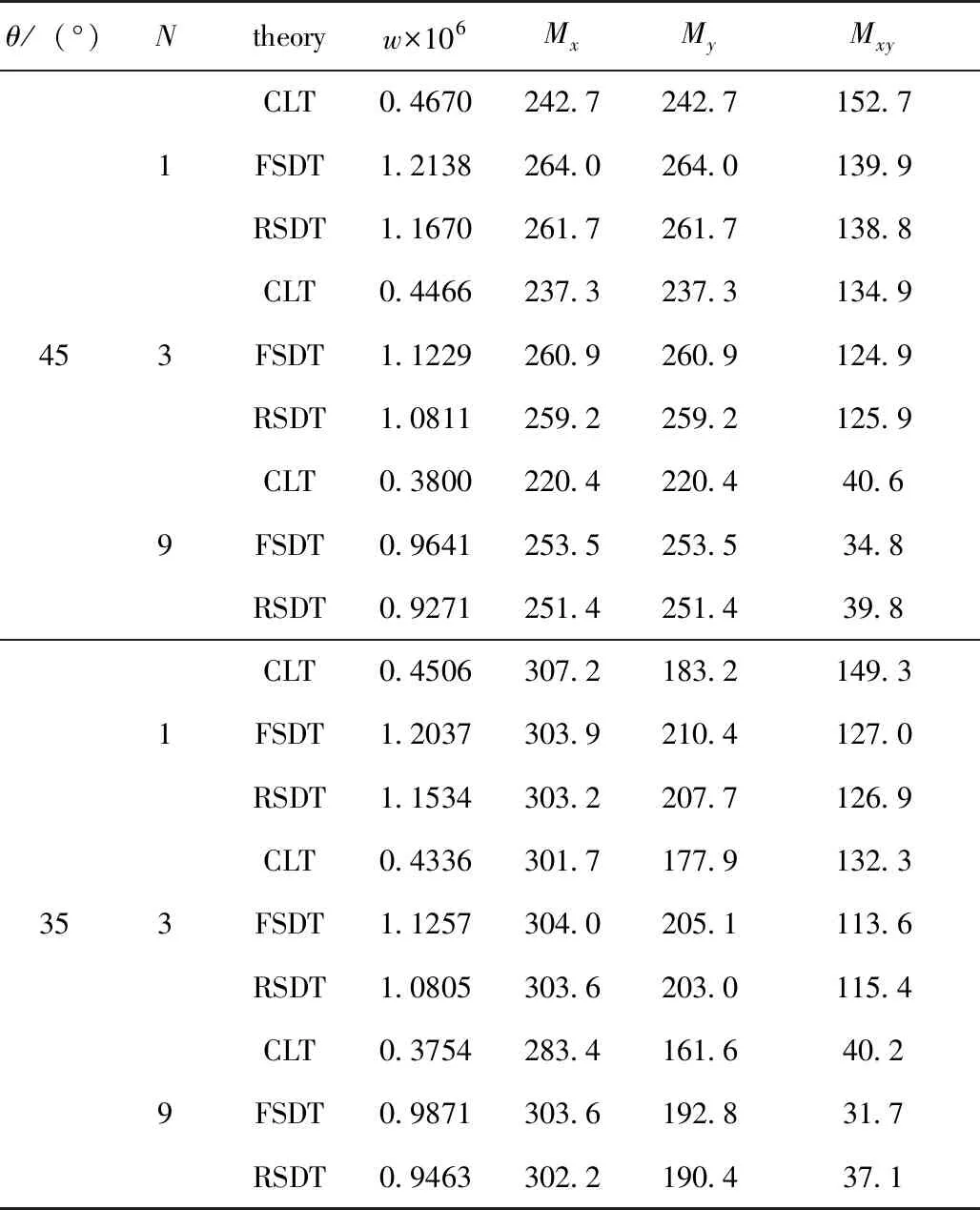
表10 四边固支层合板中心挠度、弯矩和扭矩的RSDT与FSDT、CLT计算值对比(h=0.15m,a=b=1m)

2.3 数值结果分析

通过对表7～表10的分析，可以得到以下结果：

1)横向剪切效应降低了板结构刚性。根据表1～表4，相对于经典板理论的板中心挠度值，Ressner一阶剪切理论、Reddy简化高阶剪切理论的板中心挠度值均有不同程度的增大。对于薄四边固支层合板弯曲(如h/a=0.02)，经典理论解与两种剪切理论解数值相差不大，横向剪切效应较弱，可以采用经典理论计算挠度和弯矩、扭矩。当板跨厚比h/a=0.05时横向剪切效应已不可忽略，应当按剪切理论计算挠度值，CLT理论不同程度地低估了结构挠度。

2)经典理论与Ressner一阶剪切理论、Reddy简化剪切理论计算结果存在不同程度的差异。对于四边固支层合方板中心的弯矩、扭矩，随着板厚度增加，经典理论和剪切理论(Ressner一阶剪切理论、Reddy简化高阶剪切理论)计算值差异逐渐显著起来:如h/a≤0.1时，弯矩、扭矩一般相对误差在10%以内;如h/a>0.1时，弯矩、扭矩相对误差可能超过10%，在20%之内。对于一阶剪切理论和Reddy简化高阶剪切理论而言，固支层合方板中心挠度与弯矩、扭矩计算结果基本相当，固支层合方板中心FDST的挠度值比RSDT挠度值稍大，固支层合方板中心RSDT的弯矩值、扭矩值与FDST的弯矩值、扭矩值基本相当并呈现上下波动的趋势。这表明对于四边固支层合方板，其板中心挠度、弯矩、扭矩计算采用一阶剪切理论足够精确。本文所说的Ressner一阶剪切理论是修正刚度以后的一阶剪切理论，且这一结论只对本文涉及的四边固支板中心处挠度、弯矩、扭矩计算有效。

3)铺设层数对层合板结构力学特性有较大影响。固定板厚并平均设定每层厚度，增大铺设层数N可以提高层合板的刚性和强度。具体表现为：一是增大铺设层数N，挠度值在降低，如根据RSDT理论解，对于厚度为0.1m的1层45°层合板中心挠度为0.2741×10-5m，9层[45°/-45°/45°]3对称角铺设层合板中心挠度为0.2172×10-5m，为单层板挠度的79%。二是增大铺设层数后弯矩、扭矩值在降低，扭矩值降低幅度相对更大，如根据RSDT理论解，对于厚度为0.05m的1层45°层合板中心扭矩为153.3N·m，9层[45°/-45°/45°]3对称角铺设层合板中心扭矩为41.3N·m，仅为单层板中心扭矩的27%。根据FSDT、CLT理论解计算，也能得到类似的结论。但增大铺设层数，层合板制造费用也在增加，具体层合板设计存在一个优化问题。

4)铺设角对层合板结构力学特性同样有较大影响。铺设角变化以后，层合板挠度、弯矩、扭矩都在不同程度地变化，从表1～表4均可发现这一现象。对于本文选择的四边固支边界条件，对板边界力学约束比较强，铺设角变化后各力学响应参数总体不是很剧烈，而对简支或有自由边的板结构情况会有所不同。

5)横向剪切效应和弯扭耦合效应有交联。本文引入横向剪切效应参数Ts(coefficient of transverse deformation)，以衡量横向剪切效应。

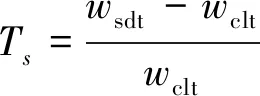
其中，wclt为经典理论的挠度值，wsdt为剪切理论的挠度值。显然，对于不考虑横向剪切效应的经典理论，Ts=0。Ts数值越大，横向剪切效应越强。以表3数据为例，对于h为0.1m的45°单层板时，根据FSDT计算板中心的Ts为0.772，根据RSDT计算板中心的Ts为0.739;而h为0.1m的35°单层板根据FSDT计算板中心的Ts为0.805，根据RSDT计算板中心的Ts为0.768。铺设角改变，板弯曲的弯扭耦合效应也随之变化，铺设角由35°增加到45°，弯扭耦合效应增大，Ts数值在下降，横向剪切效应在降低，显然这对于提高结构的刚性是有益的。对于四边固支层合方板，比较根据FSDT与RSDT计算所得的Ts，可知FSDT过度估计了板的横向剪切效应，而CLT忽略了板的横向剪切效应。

3 结论

解析法研究可过滤数值研究可能因数值方法不同带来的潜在结论不确定，本文研究实践表明了这一特点,解析法研究直接从板壳理论基础出发，比较、衡量各种板壳理论计算同一问题的精度。本文工作表明经典理论对于薄壁的复合材料板的宏观力学性能的分析是有用武之地的。对于相对厚的复合材料板，采用剪切理论计算分析是需要的。从本文研究来看，至少对于本文研究涉及的复合材料固支板，其中心的挠度和弯矩、扭矩等宏观力学性能分析，一阶剪切理论和简化高阶剪切理论计算值差异不大，这多少有些出乎预料。考虑到高阶剪切理论解析计算研究还不是很充分，本文研究复合材料板参数不够广泛，后续笔者拟再沿用解析研究的方法，针对其他方向问题和边界条件情况，再深入比较一阶剪切理论和高阶剪切理论适用范围。从理论上看，相对一阶剪切理论，简化高阶剪切理论不需要修正剪切刚度，是个先天的优点，其独特的长处应可望在具体力学计算中体现出来。

本文引入的横向剪切效应参数Ts给研究横向剪切效应提供了一种标准参数，据此发现了复合材料结构横向剪切效应与各向异性的关联特性。与各向同性板结构相比，各向异性板结构有其自身特点，有许多未知力学特点和规律待探索。本文得到的结果有的可能是共性结果，也有的可能是阶段性(或个性)结果，后续将针对其他各向异性结构力学问题继续开展研究，具体结论再行报告。文中给出一批解析计算结果，可用以校核数值计算程序。