抛物面型聚风罩内非均匀时变流场的数值模拟与实验分析

黄惠兰，梁鹏，李刚，汤维，闫桂林，文翔

(1.广西大学机械工程学院， 广西南宁530004；2.广西大学电气工程学院， 广西南宁530004)

0 引言

随着时代的发展，能源的紧缺问题已经变得不可忽视，太阳能、风能作为储量丰富、分布广泛和清洁干净的可再生能源，已经逐渐受到新能源行业的重视[1]。碟式太阳能发电系统规模小，结构紧凑,但是光电转换效率高[2]。聚风发电是提高风速来提高风力发电效率的一种技术，风力发电机的功率与风速的三次方成正比，因此，提高风速是非常有效的提高风力发电效率的方法。田德教授[3]提出了浓缩风能型风力发电技术，日本大屋裕二等[4]也于2002年提出聚风的构想，并研发了聚风发电样机，CHIPO等[5]对聚风风力发电的现有技术进行了总结，指出了其可以有效的提高低风速环境中的发电机的输出功率。但现有的浓缩型风能发电装置都存在结构复杂且能源应用形式单一的问题，为此，本文提出了一种将碟式太阳能发电技术与浓缩型风力发电技术结合为一体的抛物面聚风聚光发电装置，采用结构简单的抛物面型聚风罩，这样不仅可以实现浓缩风能，还能聚光，对太阳能进行利用。本文主要对该装置内的非均匀时变流场进行了数值分析与实验研究。

1 聚风罩内非均匀时变流场的数值分析

1.1 抛物面聚风聚光器结构

碟式太阳能聚光器受到的风压主要集中在中心处[6]。本文设计的抛物面型聚风聚光发电系统，将碟式太阳能发电系统中的聚光器中部切开一个缺口作为风力发电叶轮的安装位置，这样聚光器不仅充当着碟式聚光发电的聚光器，还同时充当着浓缩型风力发电系统中的浓缩风能装置，并且可以有效的减少抛物面聚光器受到的风压。初始设计的抛物面聚风罩焦距为600 mm，入口直径为1 500 mm。

1.2 抛物面聚风聚光装置计算模型

图1 计算区域网格划分Fig.1 Computational domain mesh

建立抛物面聚风聚光装置的几何模型，因为只考虑均匀来流时装置内的流动特性，可将其简化为非传热稳态不可压缩流体问题[7]。数值计算的基本方程采用Navier-stokes 方程，湍流模型为sst k-ω模型。

模型的计算域为半径3 000 mm，高度4 000 mm的圆柱形。因为主要考虑的是聚风罩内部的流场特性，所以聚风罩内部的网格相对控制的密一些，而聚风罩外部的网格疏一些，以节省计算时间。计算域含3 551 571个单元，634 622个节点，网格划分见图1。

采用速度入口边界条件，来流风速10 m/s；出口采用压力出口，相对静压力为 0 Pa；计算域的其他边界均为对称边界；壁面为无滑移边界条件。

1.3 计算结果及分析

沿抛物面聚风聚光器轴向取9个截面，分别为抛物面收缩段截面1～4，圆筒段截面5～9，各截面位置见表1,将计算区域沿中心线剖开得到流速等值线，如图2所示，考察抛物面聚风聚光器径向的流速情况。

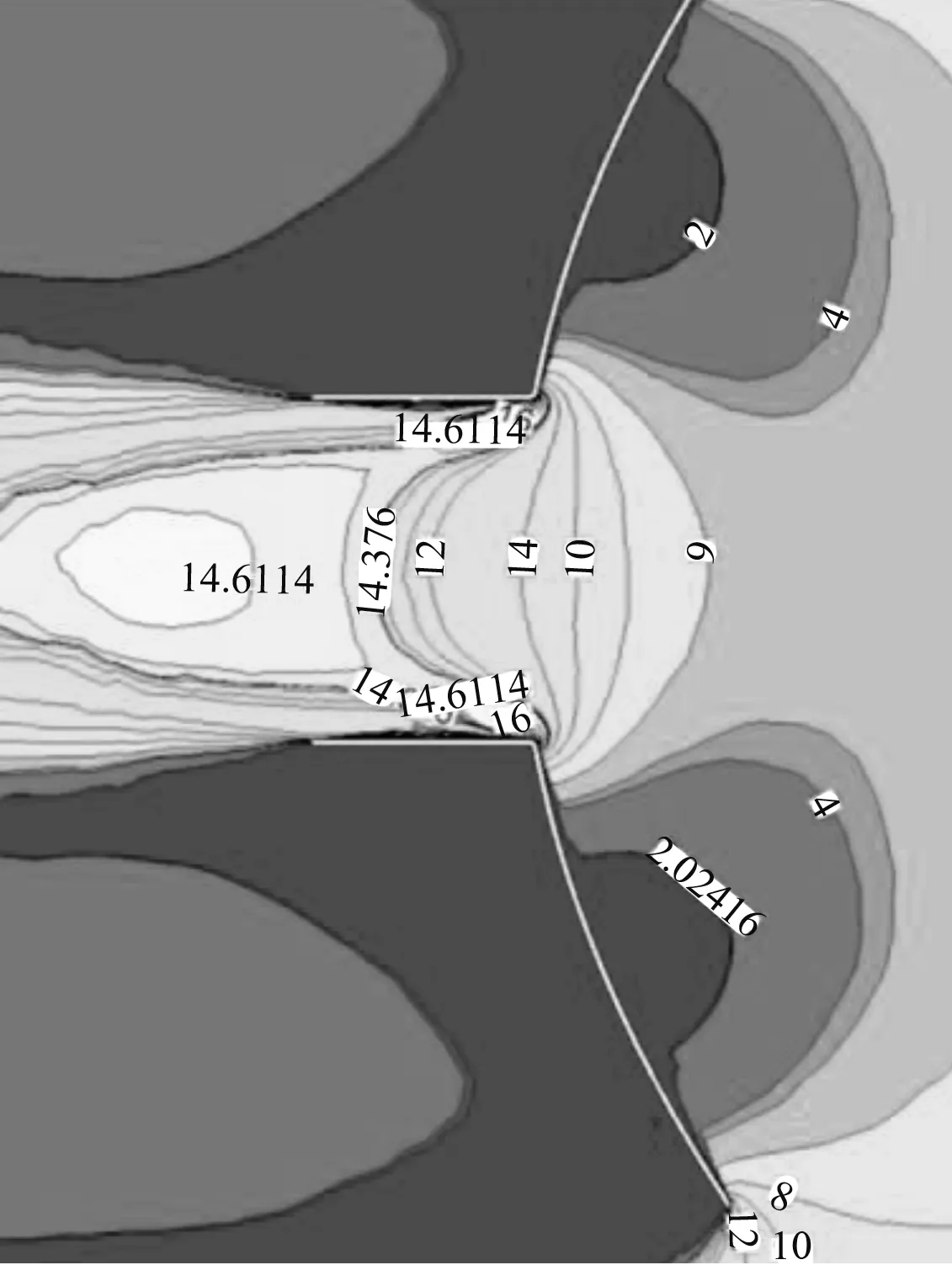
图2 流速等值线图Fig.2 Contour map of flow velocity

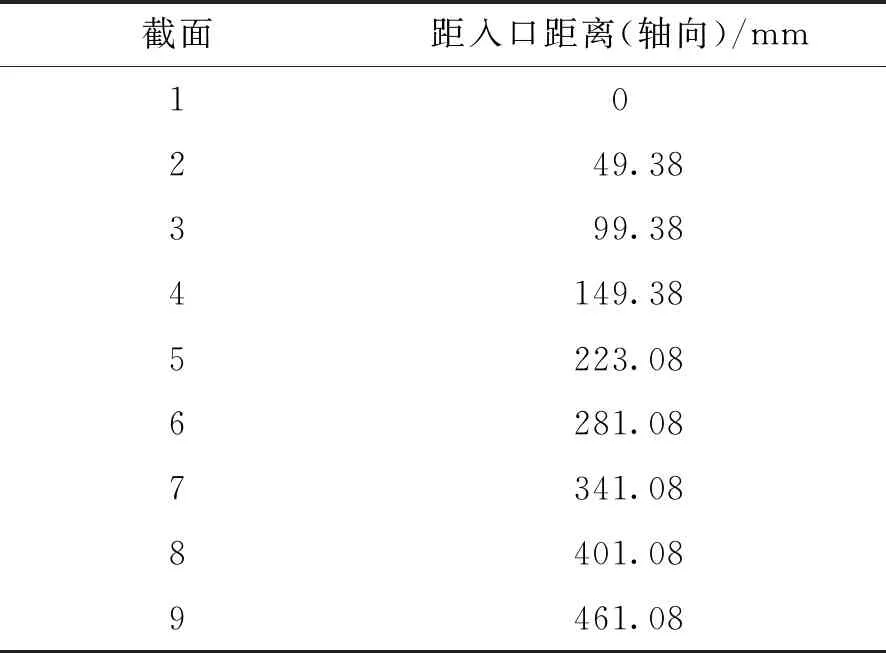
表1 轴向截面分布Tab.1 Axial cross section distribution

由于抛物面的结构特性，风并没有全部朝着中央圆筒处汇聚，来流在进入抛物面聚风罩前方区域时受到抛物面的阻挡而出现速度减小的现象。来流风在抛物面中点处出现分流，一半向中间聚风口处汇聚，一半向外扩散。在分流点处受到的压力最大，故该处的风速最小为2 m/s，风速沿着径向逐渐增大至中心轴处。在整个结构中，中央圆筒处风速最大，最高风速达到了16 m/s，有着很明显的聚风效果。浓缩装置收缩段呈现边缘流速低，且向中间慢慢增大的现象，这是因为抛物面聚风罩的结构特性，中央圆筒截面处的流速呈现边缘高中间低，这是适用于升力型风力发电机的非均匀流场特性。

聚风罩径向横截面流速分布特征如图3所示，由图3(a)可以看出，在聚风罩入口截面1处，风速先从边缘0.75(-0.75)m处的来流风速10 m/s逐渐降低至0.45(-0.45)m处的2.2 m/s，然后再逐渐增大，中心轴线处为5.7 m/s。抛物线收缩段的各截面风速变化趋势与截面1相似，且越靠近圆筒，轴线处的风速逐渐增大。这是由于抛物面漏斗状的结构特性，包裹住了大量的风，并对其形成阻挡效果，而中间由于开口的原因，风受到的阻挡作用比较小。

由图3(b)可以看得，圆筒入口处(截面5、6)的风速呈现边缘流速高，中间流速低的现象。但在圆筒后半段，接近出口处(截面7、8、9)呈现中间风速高，两边风速低的流场特性。对仿真的流场分析表明，本装置有着浓缩风能的效果，并且圆筒处的流场也符合升力型风力发电机的流场特性。

抛物面聚风装置虽然对风的流动有一定的阻挡作用，但是由于其结构特性可以兜住更多的风，所以聚风效果很明显，适用于浓缩风能发电技术。

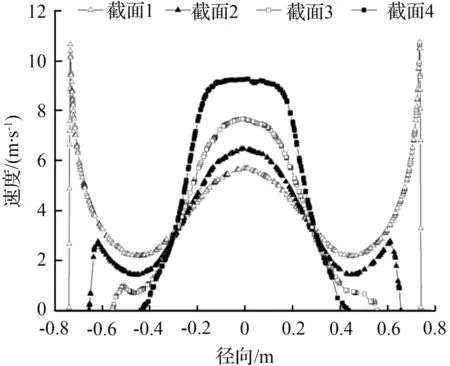
(a) 抛物面收缩段各截面上流速沿径向分布

(b) 圆筒段各截面上流速沿径向分布

图3 聚风罩径向特征横截面流速分布
Fig.3 Cross-sectional velocity distribution of radial characteristics of wind shield

2 抛物面型聚风罩试验分析

通过测量聚风装置中心轴线上的风速与模拟结果进行对比，验证其可靠性，为了方便比较，实验装置采用数值计算模型同样的尺寸。用风速仪对聚风罩中心轴线上的风速进行测量，验证数值模拟的准确性，本实验采用的是德图testo 405i手持式热敏风速仪，其测量范围为-20 ℃～+60 ℃，0～30 m/s。

2.1 实验方法

图4 试验装置图 Fig.4 Test equipment

采用4台700-4P管道式轴流风机搭建风墙作为试验的来流风场，风机的额定功率为3 kW，转速为1 450 r/min，风量为24 500 m3/h。将聚风罩置于风场的中央，与风墙距离为3 m，并在聚风罩前800 mm处用风速仪测量来流风速，以确保其达到验证试验的要求。试验装置如图4所示。

使用变频器对风机的频率进行调节以调节风速，当聚风罩前800 mm处的风度达到10 m/s时待风场稳定后，使用风速仪对聚风罩中心轴线上的风速进行测量。以聚风罩抛物面入口截面的中心点为起点，每隔80 mm设置一个测量点，共测量10个数据点的风速。

2.2 抛物面聚风罩中轴风速的测试

为提高试验准确性，共测量三组数据求平均值，来得到中心轴线上风速的实验值。实验值如表2所示：

表2 各测试点的风速测量值Tab.2 Measuremented wind speed at each test point

图5 中心轴线上的风速比较 Fig.5 Comparison of test simulation data

比较模型中心轴线上的风速与实验结果，如图5所示。

由图5可知，计算结果与实验结果趋势一致，计算得二者的最大误差为9.7 %，在可以接受的范围内，说明所用的模拟方法可行。

3 抛物面聚风聚光器的结构参数影响分析

碟式聚风罩是碟式太阳能聚风聚光发电系统中的主要部件，其结构对整机的输出功率有着很重要的影响，在保持抛物面入口直径为定值1 500 mm的情况下，通过对不同焦距及不同中央开口大小进行结构分析，得出使能源利用率达到最大的最佳结构。

3.1 抛物面聚风聚光器管道半径的影响

碟式聚光器充当着聚光器和聚风罩两个身份，故对聚光器的优化要考虑到聚风聚光两个方面，而随着聚光器中央开口的增大，其对聚光效果的影响要远小于其聚风效果的增益，所以这里对抛物面聚风聚光器的聚风效果进行优化。抛物面中央开口的半径即为圆筒的半径，而圆筒半径不同代表着风机叶轮的大小也不同，所以这里考虑的优化量是能量，而不是风速。单位时间内通过某一截面的风能计算公式为：

(1)

其中，W为风能，W；ρ为空气密度，kg/m3;ν为风速，m/s；S为风速截面积，m2。

在焦距相同时，对不同管道半径进行模拟。当焦距为600 m时，分别对管道半径为200 mm至700 mm间的聚风装置进行计算，取中央圆筒入口处截面的平均风速计算风能，结果如图6所示。由图6可知风能在开口600 mm处达到峰值，为1 202.4 W，而后逐渐减小又增大至没有聚风结构的1 081.8 W，所以在开口半径为600 mm时，在中央圆筒入口处，抛物面聚风后的风能最大。

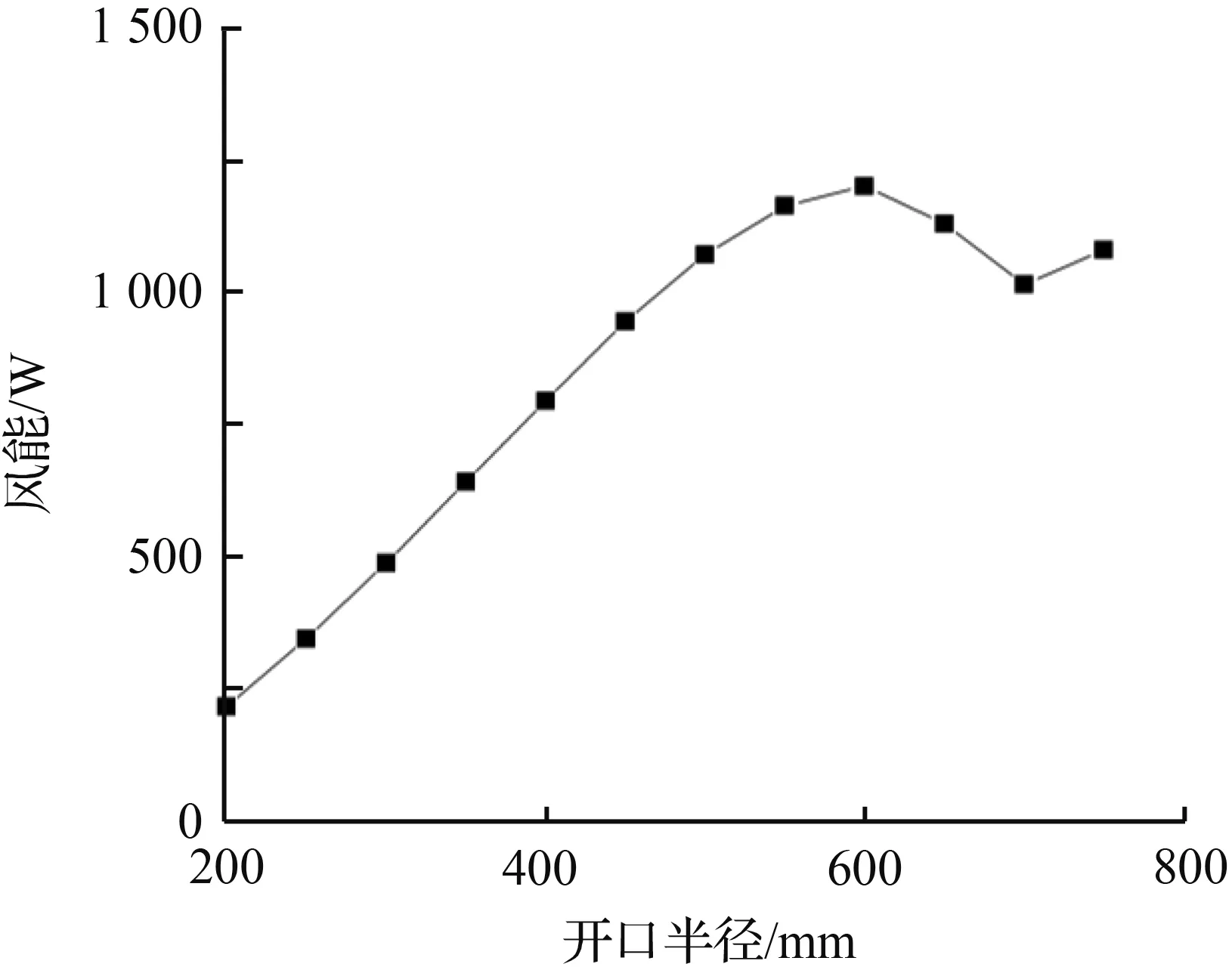
图6 开口半径对风能的影响
Fig.6 Influence of opening radius on wind energy

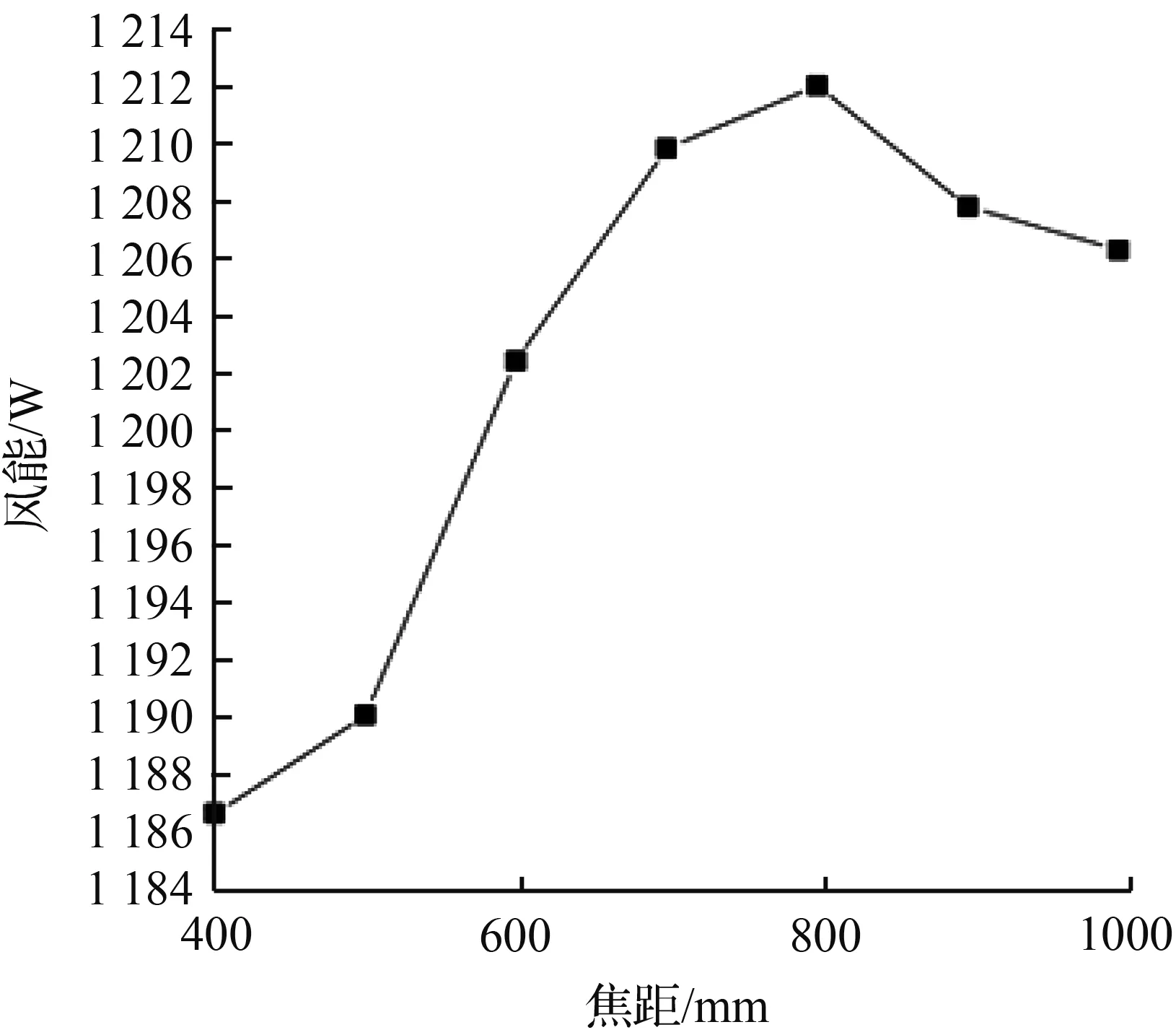
图7 焦距对风能的影响
Fig.7 Effect of focal length on wind energy

3.2 抛物面聚风聚光器焦距的影响

当抛物面入口直径确定，圆筒的直径确定，不同的焦距代表着不同的抛物面聚风罩的长度。由“3.1节”的结果可知，聚风之后，最大的能量值出现在圆筒半径为600 mm，现对焦距为400 mm至1 000 mm时，开口半径为600 mm的聚风罩进行流场模拟。结果如图7所示，由图7可知，当焦距为800 mm时，风能达到最大值为1 212.04 W，截面平均风速为12.05 m/s。

4 聚风装置内的旋转机械模拟

4.1 聚风条件下的叶轮设计

叶片设计是风力发电技术重要的一部分，主要包括气动与结构设计[8]。而叶轮的功率与风速的三次方成正比，所以风速是叶轮设计中的一个重要条件[9]。置于聚风装置内的叶轮受到聚风罩内非均匀时变流场的影响，其设计风速也对流场的非均匀性进行考虑。发电机风轮功率计算式为：

(2)

其中，P为风轮输出功率，W；Cp为风能利用系数；ρ为空气密度，kg/m3；ν为风机上游风速，m/s；A为风轮扫风面积，m2。

在第2、3节得到的最佳聚风罩结构基础上，本文采用Wilson模型[10]设计非均匀流场下的风力发电机叶片，即非均匀流场的特性，对处于不均匀流场中不同位置处的叶片叶素采用该处的风速进行设计。翼型采用NACA-4412，选取叶片长度为0.53 m，轮毂半径为0.05 m。根据计算得到叶片各截面的弦长与扭角。

4.2 带叶轮的聚风装置的滑移网格处理

滑移网格是属于动网格的一种特殊形式，其网格节点在给定的动态区域内做刚性移动，相对于一般的动网格，它不需要进行网格重构，节省了计算机资源，并且运动过程中整个计算域网格的品质不发生任何变化，避免了负体积网格的出现[11]。滑移网格技术中关于标量φ的守恒方程为：

(3)

当使用一阶后向差分公式时，时间导数向可以表达为：

(4)

体积的时间导数为：

(5)

用一小圆柱体包裹住叶轮作为旋转域，外部用大圆柱包裹住聚风装置与旋转域作为静止域，旋转域存在于静止域内部，二者通过三对interface连接，为了防止流体因区域间的过度而受到影响，对interface处的网格要求比较高。

4.3 计算结果及分析

用非稳态算法进行滑移网格计算，设定旋转域的转速为144.8 rad/s，时间步长为0.000 43 s，计算500个时间步，监控叶轮的扭矩系数。计算完成时，扭矩系数稳定可认为计算已经收敛。

由图8可以看出，叶轮正负面存在着很明显的压差，这正是推动叶轮进行旋转的动力。将计算结果导入CFD-POST中，利用torque公式计算得到叶轮Y轴上的扭矩为-2.18 N·m，与转速相乘可得功率为222.0 W。对同直径的浓缩型风力发电机与普通风力发电机的输出功率进行比较，是验证浓缩风能效果的一种方法。由参考文献[12]可知300 W普通型风力发电机的功率输出特性，利用功率与叶轮直径平方成正比的关系将其换算成直径为1 200 mm时的功率，结果如表3所示。利用滑移网格技术对聚风装置内叶轮在不同的自然风速下进行旋转机械模拟，得到功率输出特性。

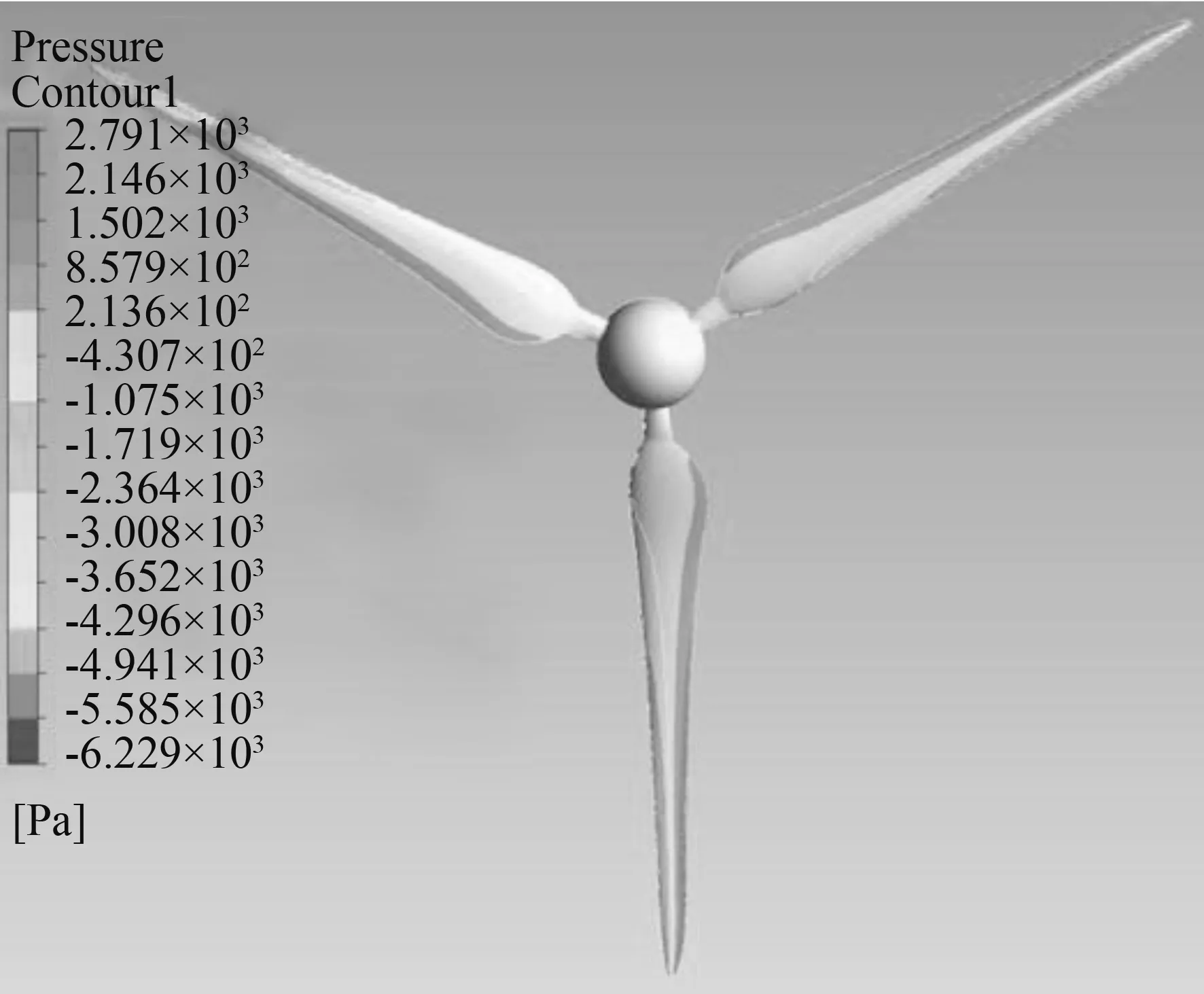
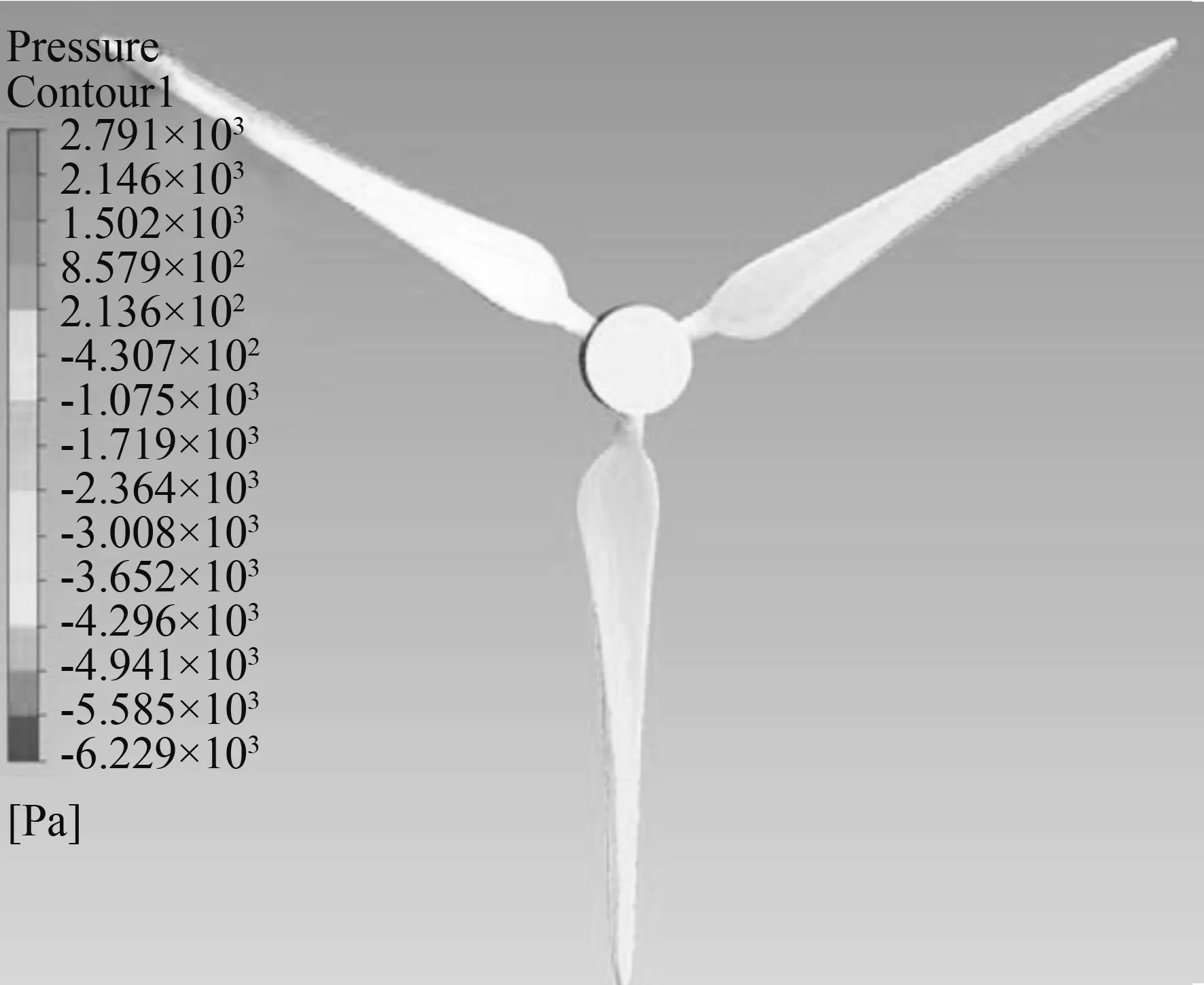
图8 叶轮正负表面压力图Fig.8 Surface pressure of impeller

10 m/s的自然来流风经过抛物面型聚风罩的浓缩风能作用后，在叶轮前的截面平均风速为12.05m/s，而本文考虑到抛物面聚风罩内流场的非均匀性设计的叶片，使得抛物面型聚风罩内的风力发电机功率较同直径下的普通型风力发电机有着很明显的提高。其结果分别如表3、表4所示。由表3、表4可得知，抛物面聚风罩内的叶轮在自然风速为10 m/s时，输出功率为222.0 W，同直径下的普通型风力发电机的输出功率为100 W，功率相对提高了122 %。可见抛物面聚风罩对风能品级的提高效果显著。

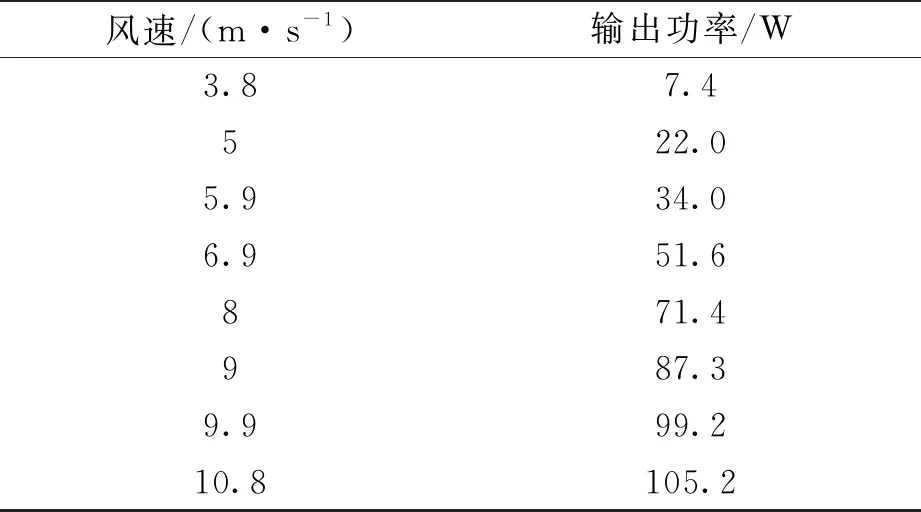
表3 300 W 普通型风力发电机功率输出特性Tab.3 Power output characteristic of 300 W wind energy turbine

表4 聚风罩内的叶轮功率输出特性Tab.4 Power output characteristics of the impeller in the poly hood

5 小结

提出一种集风能、太阳能利用于一体的发电装置，通过数值模拟与试验分析，验证了该新型蝶式聚光聚风发电系统的聚风性能，运用滑移网格技术对装置内的叶轮旋转情况进行了仿真研究，主要得到以下结论： ①抛物面聚风聚光装置收缩段边缘流速低，中间慢慢增大的现象，这是抛物面的结构特性导致的；②在原设计的基础上，对抛物面聚光聚风罩的结构进行优化，得知当抛物面的焦距为800 mm，中央开口半径为600 mm时，抛物面聚风罩聚风后的风能最大，为最佳结构；③利用Wilson模型设计了非均匀时变流场内的风机叶轮，并用滑移网格技术对抛物面聚风聚光装置内叶轮进行了旋转机械模拟，计算结果表明在自然风速为10 m/s时，叶轮的输出功率为222.0 W，与同直径下的普通型风力发电机相比，功率提高了122 %。