一类有限变时滞微分系统的一致渐近稳定性研究

丁黎明

（江苏财会职业学院 基础部，江苏 连云港 222061）

时滞现象在自然科学与社会科学的许多学科中普遍存在，如核物理学、电路信号系统、遗传问题、商业销售问题、工业生产管理等。人们从事各种生产实践活动要求所在的系统都能够保持时滞的稳定性。各种工程系统中特别是自动控制系统的时滞现象更为普遍，近年来微分系统的稳定性问题逐渐引起国内外控制界的关注[1-5]。由于在实际问题中，系统会受到各种各样的干扰，时滞也会受到各种各样的影响以随时间的发展而变化，因此研究变时滞微分系统具有更多的现实意义，取得了广泛的研究成果[6-15]，许多学者对无界变时滞系统解的稳定性也进行了深入研究[16-18]。下面利用Lyapunov方法和稳定性有关理论[19-20]，研究一类有限变时滞微分系统零解的一致渐近稳定性。

1 引理

考虑RFDE(f)

其中f∈C(R×C,Rn)，假定(1)满足解的整体存在与唯一性条件。

引理 1[1]设u,v∈k,w:R+→R+，若存在一个R×C→R的连续泛函V(t,φ)使得存在反函数，记。

定理1 如果存在正数β1，β2，…，βn及ω使得

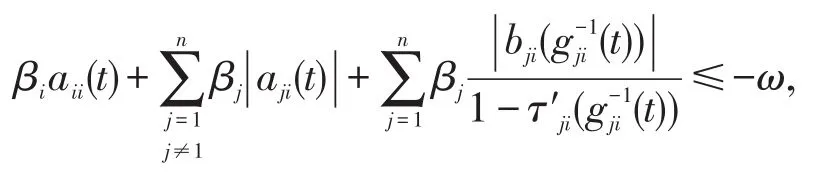
对t∈R+都成立，则系统(2)的零解是一致渐近稳定的。

证明构造Lyapunov泛函

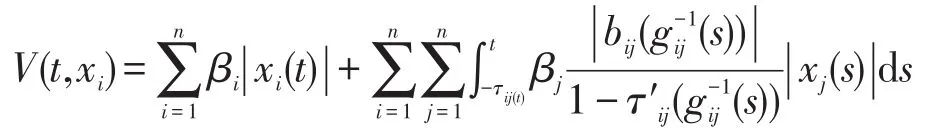
则V(t,xi)沿系统(2)的解的导数为

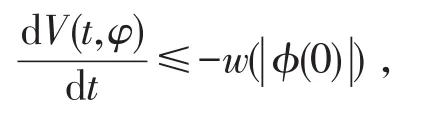
则方程（1）的零解是一致稳定的。若当s＞0时w(s)＞0，则方程（1）的零解是一致渐近稳定的。

2 线性系统的一致渐近稳定性

考虑具有限变时滞的线性微分系统

其中aij(t)，bij(t)都是R+上有界连续函数，τij(t)是R+上非负有界可微且 0≤τ′ij(t)＜1，gij(t)=t-τij(t)

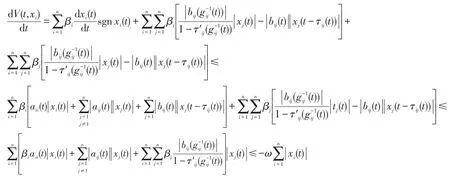
由aij(t)，bij(t)的有界性可知，存在常数K＞0，使得

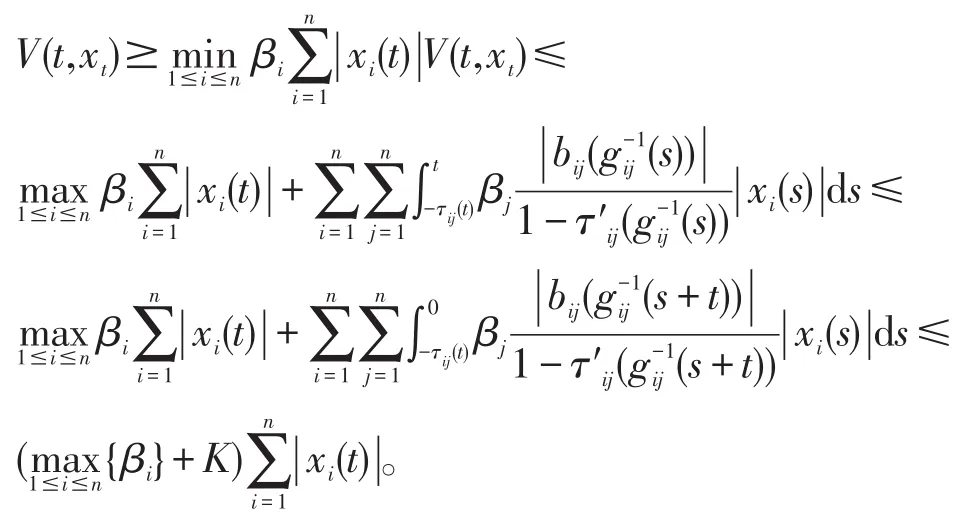
因此由引理1可知系统(2)的零解是一致渐近稳定的。

唯一，Fi(t,0,…,0,0,…,0)=0,τij(t)在 R+上非负有界可微且 0≤τ′ij＜1，gij(t)=t-τij(t)存在反函数，记。

如果存在R+上非负有界连续函数aij(t)(i≠j)，bij(t),i,j=1,2,…,n，使得

对t∈R+都成立。我们有

定理2如果存在正数β1，β2，…，βn及ω使得

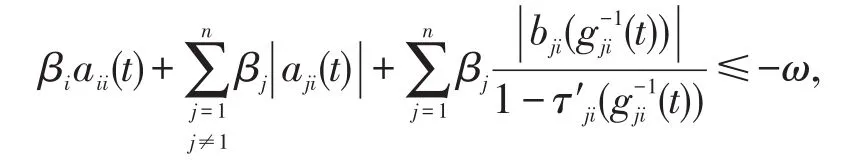
对t∈R+都成立，则系统(3)的零解是一致渐近稳定的。

证明构造Lyapunov泛函

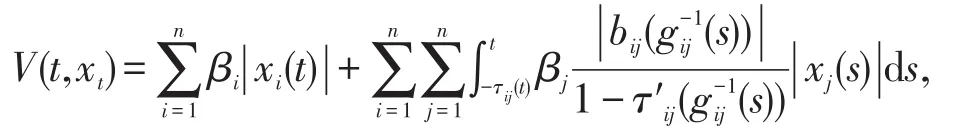
3 非线性系统的一致渐近稳定性

考虑具有限变时滞的非线性微分系统

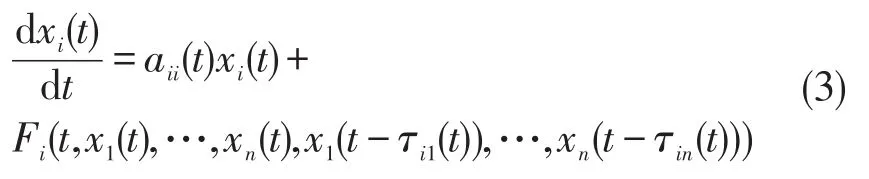
其中aii(t)都是R+上有界连续函数，Fi:R+×Rn×Rn→Rn连续，满足初值问题解的存在则V(t,xi)沿系统(3)的解的导数为

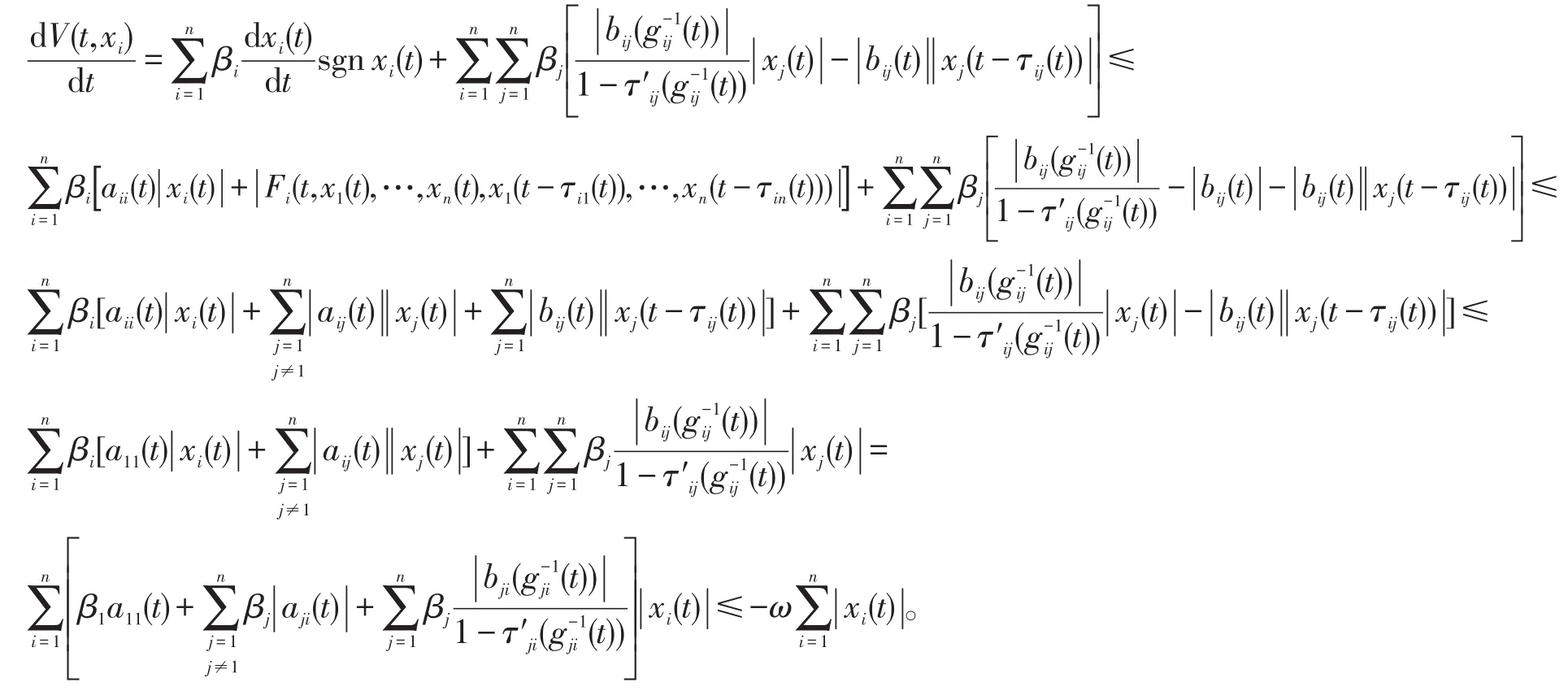
因此由引理1可知系统(3)的零解是一致渐近稳定的。

4 小结

在实际模型中，要准确地描述客观实际，就必须考虑随时间的发展而变化的时滞影响，从而进一步的建模、设计、分析和应用。人们可以通过时滞来控制系统的稳定性，进而运用到控制理论中的反馈系统去探讨有关问题。当研究的系统情况更复杂，具多元与叠加性时还可讨论无限时变时滞系统的稳定性问题。