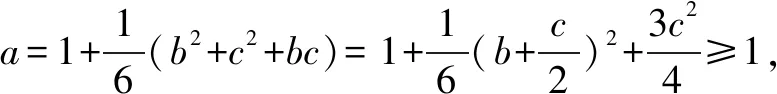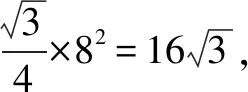数学解题需重视培养八种“非常规”意识

蔡勇全

(四川省资阳市外国语实验学校 641300)

一般来说，各种数学问题都有适合它的最基本的解答策略与思路，即所谓的“常规解法”或“通性通法”，这也是我们日常教学的重心所在.但我们也应该清醒地认识到，一方面，高考命题越来越重视考查学生的思维能力和知识的迁移能力；另一方面，对于有的数学题目，若仅按常规方法来处理，不但过程繁琐冗长，费时费力，事倍功半，而且极易出现错误，甚至有时难以凑效.此时若转换思维视角，运用“非常规”策略解答，往往思路新颖，方法巧妙，过程简明，事半功倍，起到了化难为易的效果.基于此，笔者认为，学生仅仅掌握基本的解题思路和常规技巧是不够的，还需在对基础知识、基本技能、基本思想方法掌握的基础上，培养其具备适当的“非常规”解题意识，掌握一些“非常规”的解题技能，帮助其培养思维的灵活性、发散性和多样性.本文结合实例谈一谈数学解题需要培养的八种“非常规”的意识，以期抛砖引玉并引起重视，供大家参考.

一、递推意识

数学中的递推关系是反映问题内在联系的一种形式.许多与正整数有关的组合几何、实践操作等问题，表面看似乎与递推式毫无联系，实际上，当我们仔细挖掘题目中的隐含信息，巧妙构造递推关系，然后对递推式进行适当的变形处理，是能够实现有效、快捷的解题目的的.

例1 有一楼梯共10级，每步只能跨上1级或2级，问要登上最后一级共有多少种走法？

解析因为每步只能跨上1级或2级，所以最后一步可能从第9级也可能从第8级跨上第10级，向前递推关系不变，设登上第k级有ak种走法，显然a1=1，a2=2，当k>2时，登上第k级台阶的走法可以分两种情况得到:从第k-1级台阶跨一级登上第k级，或从第k-2级台阶，一步跨两级登上第k级，故当k≥3时，有ak=ak-1+ak-2，所以a10=a9+a8=2a8+a7=…=34a2+21a1=89.

变式1四人互相传球，由甲开始发球，并作为第一次传球，经过6次传球后，球仍回到甲手中，那么共有多少种传球方式？

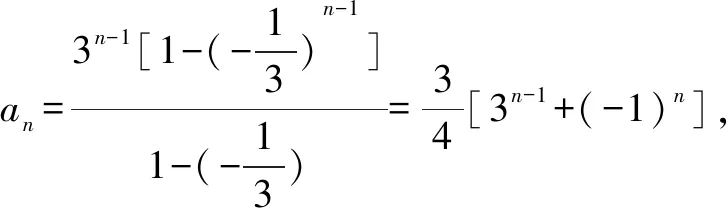
变式2 平面内有n个圆，其中每两个圆都相交于两点，且任意三个圆不相交于同一点，求证:该n个圆把平面分为n2-n+2部分.

提示设n个圆把平面分为an部分，再增加一个圆C，根据题意新增加的圆C和原来的n个圆有2n个不同的交点，这2n个交点把圆C分为2n段圆弧，这2n段圆弧又把原来的一部分分为了两部分，因此an+1=an+2n，即an+1-an=2n.因此an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=2+2[1+2+…+(n-1)]=2+n(n-1)=n2-n+2.

评注表面上看，上述题目仿佛属于排列组合范畴，但在精心提炼题意后将其转化为递推数列问题，不能不说，这样的处理方式让人耳目一新.从递推角度分析处理问题，关键是要根据题意找到能揭示问题内在联系的递推关系，在此基础上利用数列的知识进一步解决问题.当然，在不同的问题中应该归纳不同的递推关系.

二、反推意识

有些数学问题，若按常规思路直接从正面寻求解答，往往由于无法找到解题思路而使思维一时受阻或需要考虑的因素太多致使求解过程纷繁冗长，这时若调整思维方式，从问题的反面进行推证，往往能使陷入僵局的解答思路“柳暗花明”，达到化繁为简、化难为易的解题效果.

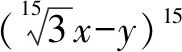
分析若正面求解本题，必须从二项式的展开式出发，先找出所有无理数系数，再求其和，这显然十分麻烦.若从反面思考，先研究二项式的展开式中所有有理数系数，不难发现，其中含有有理数系数的项只有两项.

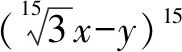
变式1已知集合A={(x，y)|y=4x2-2(p-2)x-2p2-p+1}，B={(x，y)|-1≤x≤1，y>0}，若A∩B≠∅，求实数p的取值范围.

变式2λ为何值时，二次方程(1-i)x2+(λ+i)x+1+λi=0(λ∈R)有两个虚根？

提示二次方程有两个虚根，即无实数根，若将能使方程有实根的λ的值排除，即得本题的结果，所以先求使方程有实根的λ的值.若方程有实根，设α是方程的实根，则(1-i)α2+(λ+i)α+1+λi=0，即(α2+λα+1)+i(-α2+α+λ)=0.因为α，λ∈R，所以α2+λα+1=0，且-α2+α+λ=0，两式相加可得(α+1)(λ+1)=0，解得λ=-1或α=-1.若λ=-1，则α2-α+1=0无实根，舍去；若α=-1，则λ=2，即当λ=2时方程有实根.故当二次方程(1-i)x2+(λ+i)x+1+λi=0(λ∈R)有两个虚根时，λ∈R且λ≠2.

评注反推意识实质上就是一种逆向思维、补集意识，其常见的表现形式就是“正难则反”，它极大地简化了运算，避免了繁琐的过程，明显提高了解题效率.

三、配对意识

某些数学问题，从一般思路入手，常常由于繁琐的运算而极易出错，甚至思维受挫，这时需及时调整解题视角，如根据题设条件或所求结论中某些式子的结构特征，联想并构造出能与之形成和与差、积与商、正与负、互为有理化因式、互为共轭因式、正弦与余弦、正切与余切、奇函数与偶函数等配对的代数式，然后将这两个配对式通过合理的变换与运算，简捷高效地完成问题的解决，使陷入僵局的解答过程“拨云见日”.

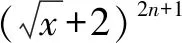
变式1已知实数x，y满足x2-3xy+y2=2，求x2+y2的取值范围.

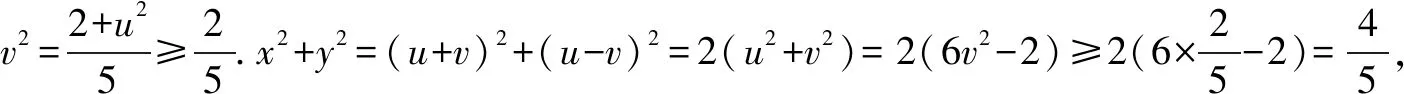
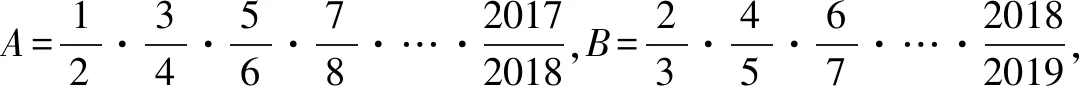
评注通过构造配对式解决相关数学问题，不仅可以极大地减少运算量，优化解题过程，起到化繁为简、化难为易的效果，而且可以较好地体现数学的对称美、奇异美、和谐美与统一美.

四、方程(不等式)意识

方程与不等式犹如一对“孪生兄弟”，可以说是最普通、最常见的两个数学对象，二者看似平凡熟悉，但常常并不是最先为大家所想到的解题媒介，因而从这个方面来说，它们并不常规.有时题目中各类元素之间的内在联系通过方程或不等式抽象出来，借助方程或不等式的知识，可以很快得到所要求的结果.

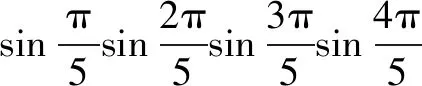
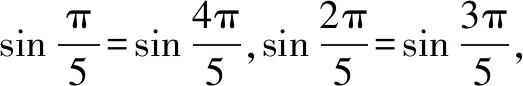
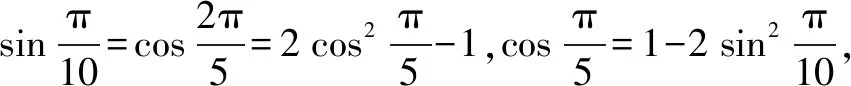
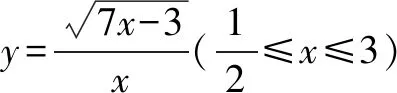
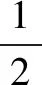
变式2一个口袋内装有4个不同的红球，6个不同的白球，若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的取法有多少种？

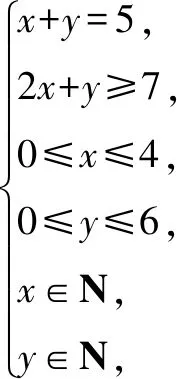
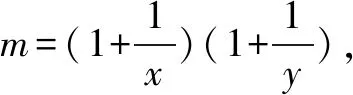
评注方程(不等式)意识实际上是从构造角度解答问题，是一种创造性思维，带有试探性和不规则性，根据题设条件的特征、运用数学语言将问题转化为方程或不等式模型是解决此类问题的关键.

五、夹逼意识

夹逼意识是指在解决某些数学问题时，可由题意列出若干个不等式，在解题中，然后运用夹逼性质“挤”出某个变量的值，从而实现由不等向相等、由变量向常量的转化，这是在“不等”中寻找“相等”的重要途径.这种意识的外在表现常常是：若a≥x0且a≤x0，则a=x0；若A≤B≤C且B∈Z，则可得到B的整数值.

例5已知函数f(x)的定义域为R，f(1)=1，对任意x∈R，都有f(x+5)≥f(x)+5，f(x+1)≤f(x)+1，若g(x)=f(x)+1-x，则g(2018)=.

解析因为f(x+5)≥f(x)+5，所以f(x+5)-5≥f(x)，从而有f(x+5)+1-x-5≥f(x)+1-x，即g(x+5)≥g(x)①.又因f(x+1)≤f(x)+1，所以f(x+1)-1≤f(x)，从而f(x+1)+1-x-1≤f(x)+1-x，即g(x+1)≤g(x)②.由①、②知，g(x)≤g(x+5)≤g(x+4)≤g(x+3)≤g(x+2)≤g(x+1)③.又由②知，g(x)≥g(x+1)④，所以由③、④可知，g(x+1)=g(x)对任意x∈R都成立.因此g(x)是周期为1的周期函数，从而g(2018)=g(1)=f(1)+1-1=1.

变式1已知函数f(x)的定义域为R，f(0)=2016，对任意x∈R,都有f(x+2)-f(x)≤3·2x，f(x+6)-f(x)≥63·2x，则f(2016)等于( ).

A．22014+2013 B．22015+2014

C．22016+2015 D．22017+2016

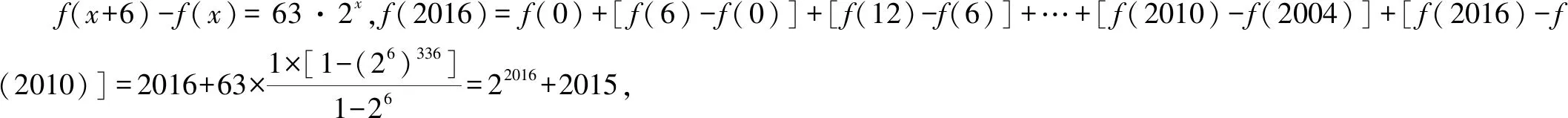
变式2已知a，b，c∈N，且29a+30b+31c=336，则a+b+c=( ).

A.10 B.12 C.14 D.16

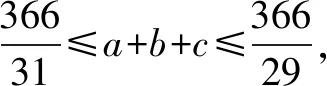
评注从上面的实例可以看到，利用“夹逼”可以挖掘得到一些隐含信息，运用“夹逼”使问题得到实质性的突破.当然，根据题设条件创造性地挖掘隐含的不等关系列出不等式是夹逼策略能否成功运用的关键.

六、添凑意识

添凑意识是指在解题过程中，要善于观察，通过恰如其分的添与凑，使问题考查的实质变得清晰、明了，从而使问题的解决变得容易.一般来说，添与凑总是相辅相成、互为依托、互为补充的，恰当的添与凑，不仅会给人赏心悦目的感受，而且会使解答事半功倍.

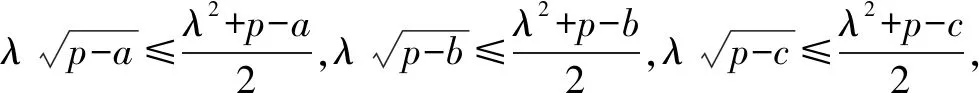
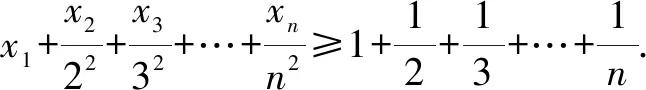
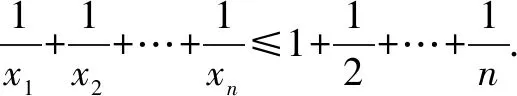
变式2 已知正数x，y满足3x+2y=xy，求2x+3y的最小值.

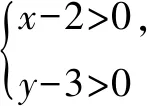
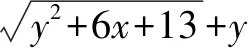
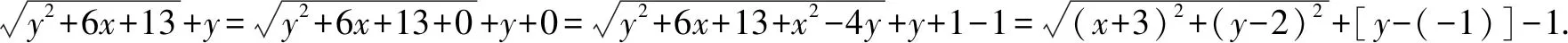
评注通过上面的实例，我们不难看到，从添凑视角解答问题，需要解题者适当具有洞穿问题本质的能力，只有不断锤炼这样的能力，才能在需要添或凑的地方运用自如、妙笔生花，而不至于画蛇添足.

七、对应意识

对应意识源自于教材中的一个重要概念——映射，当题目中研究的对象数量较多，而且它们满足的条件具有比较统一的规律性，此时不妨从对应视角切入，抓住局部或个体的一致性要求，将这种要求转化为数量关系并推而广之.

例7圆周上有15个不同的点，过任意两点连一条弦，这些弦在圆内的交点最多有____个.

变式1在平面直角坐标系xOy中，x轴的正半轴上有5个点，y轴的正半轴上有3个点，将x轴正半轴上这5个点和y轴正半轴上这3个点连成15条线段，这15条线段在第一象限内的交点最多有( )个.

A.105 B.35 C.30 D.15

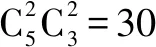
变式2从正方体的八个顶点中任取三个顶点作三角形，其中直角三角形的个数是( ).

A.56 B.52 C.48 D.40

提示由正方体的四个顶点所确定的每一个平面都对应四个直角三角形，而正方体的顶点所确定的平面共有12个，因此所求的直角三角形的个数为48个，故应选C.

变式3从集合P={1,2,3,…,10}选出5个数组成的子集，且子集中5个数的任两个数之和都不等于11，则这样的子集有( )个.

A.32 B.48 C.96 D.112

提示集合中的两个数之和等于11的数可形成一种对应关系:(1,10)，(2,9)，(3,8)，(4,7)，(5,6).因而选出5个数中的任两个数之和都不等于11，这5个数应分别从上述的每组数中各取1个，因而所求的子集个数为25，故应选A.

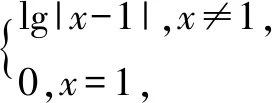
A.b<0且c>0 B.b>0且c<0

C.b<0且c=0 D.b≥0且c=0

提示令t=f(x),将方程f2(x)+bf(x)+c=0与t2+bt+c=0相对应，设方程t2+bt+c=0的两根为t1,t2，结合函数f(x)的图象，易知关于x的方程f(x)=m(m>0)有4个实根，关于x的方程f(x)=0有3个实根，所以t1>0,t2=0,t1+t2=-b>0,t1·t2=c=0，即b<0且c=0，故应选C.

评注从上面的实例中可以看到，找准量与量之间的对应关系并合理利用它乃解题的关键，抓住了这一关键，就抓住了问题间联系的纽带，就能使解题的线索迅速明朗，使解题的思路更加清晰.

八、估算意识

估算，顾名思义，估摸着计算，是以正确的算理和对所研究的问题的本质已深刻理解为基础，通过大体估值、合情猜想或特值探路等手段，进行粗略、近似的计算而获得正确答案的过程.在数学解题中渗透估算意识，有效地避开了以往“小题大作、费时费力”的逻辑推理过程，达到了简洁、快速、合理、准确的解题目的，恰到好处地契合了当前高考命题倡导的“多考点想、少考点算”这一基本理念.

例8 若实数x1满足方程2x+2x=5，实数x2满足方程2log2(x-1)+2x=5,则x1+x2的值可以是( ).

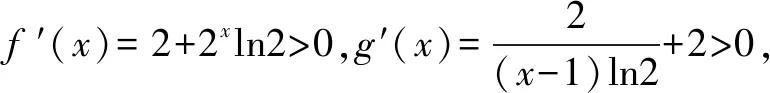
A.一切实数 B.a≤1或a≥9 C.0

变式2已知三棱锥P-ABC的侧面与底面所成的二面角均为60°，底面三角形三边长分别是7,8,9，则此三棱锥的侧面面积为( ).

变式3三棱柱ABC-A1B1C1的所有棱长均为a，且侧面A1B1BA⊥底面A1B1C1，则直线C1B与平面A1B1BA所成角的范围是( ).

评注以上实例不仅可以从估算角度得到解决，事实上，也能用其它一些方法予以解决，但相比之下，用估算法解决这一系列客观题更显得事半功倍.因此在平时学习中要注意多观察、多积累、多巩固，让估算成为重要的辅助解题手段.