Bloch型空间到调和权Dirichlet型空间的复合算子
刘佐灵
(汕头大学理学院,广东 汕头 515063)
0 引言
在Cowen和MacClue的著作中[1],具体讨论了复合算子在某些函数空间上的有界性和紧性的问题.在文献[2]中,解决了经典Hardy 空间和Bergman空间上的复合算子的有界性紧性问题.Shapiro 在文章[3]中首次引入了复合算子的本性范数.近年来,复合算子在各类函数空间上的问题得到了丰富发展.其中与Bloch空间相关的复合算子的文章有文献[4-10].与Bloch 空间相关的关于复合算子的本性范数刻画的文章有文献[11-13].本文主要也是考虑从Bloch 型空间出发到新一类空间的复合算子,主要讨论在其上的有界性、紧性和本性范数的问题.
2005年,乌兰哈斯在文献[8]中讨论了Bloch 空间到Qk空间的紧性问题.2007年,Marko Kotilainen 在文献[5]中研究了复合算子从Bloch 型空间到Qk型空间的有界性和紧性问题.2009年,Jordi Pau 在文献[7]中考虑了复合算子从Bloch 型空间到Qk型空间的本性范数的问题.从以上文章中受到启发,本文主要考虑复合算子从Bloch 型空间到调和权Dirichlet 型空间上的有界性、紧性和本性范数的问题.
1 准备知识
如果f∈H(D),且范数定义为
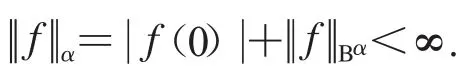
其中
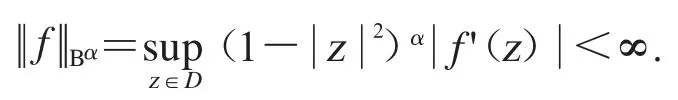
1991年,S.Richter 在文献[14]中引入了调和权Dirichlet 型空间D(μ).设μ 为圆周T 上的正Borel 测度,其中
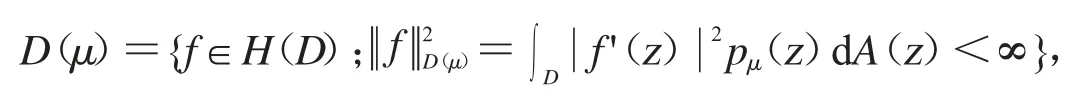
而dA 为单位圆盘上的Lebesgue 测度,其中
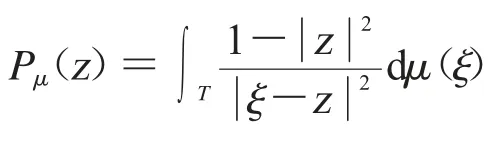
是在单位圆盘D 上关于μ的Poisson 积分.对Dirichlet 空间感兴趣的读者可以学习专著[15].
注:如果存在两个常数C1和C2使得C1A2≤A1≤C2A2,那么我们就说A1和A2等价,记作A1≈A2.Bx记作Banach 空间上的单位球.
2 引理及主要结果及其证明
引理2.1[16]设α>0 和为缺项级数,存在常数C>1 和所有K∈N,有nk+1≥Cnk.那么
(1)f(z)∈Bα当且仅当
引理2.2[17]设0<α<∞,如果{nk}是一个递增的正整数数列且对所有k的都满足设0<p<∞,那么存在一个只和有关的常数A,使得
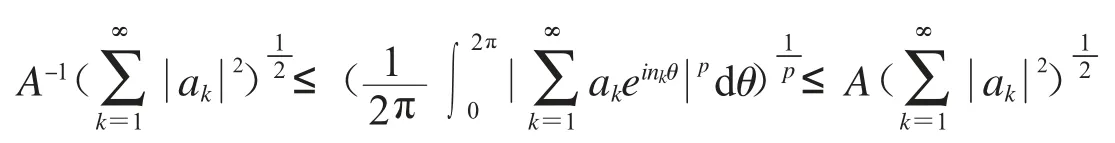
成立,其中{nk}为复平面上的任意数列.
定理2.3 设φ 为单位圆盘上的解析自映射,那么如下叙述彼此等价:
(1)Cφ:Bα→D(μ)是有界的;
证明:我们首先证明由(3)推出(1).对于所有的f∈Bα我们有
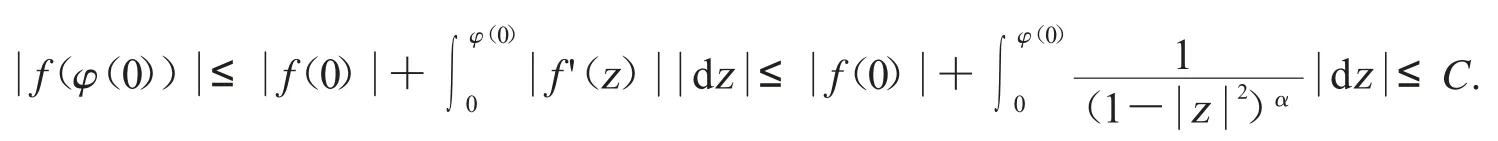
接下来我们证明对所有的f∈Bα且限定时,有如果f∈Bα,我们有
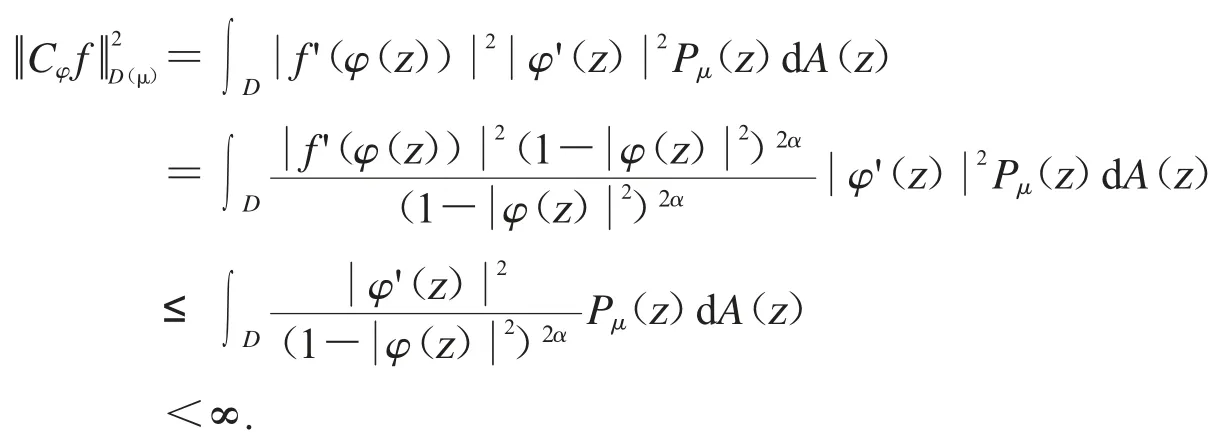
从而证明了(3)推出(1).
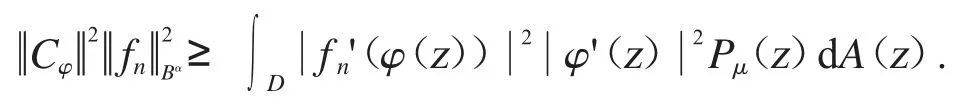
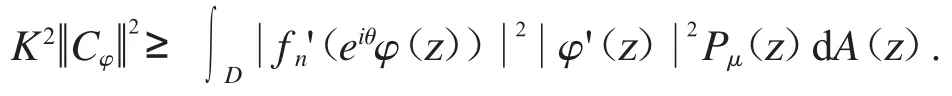
不等式的两边都对θ 进行积分和应用Fubini’s 定理可得
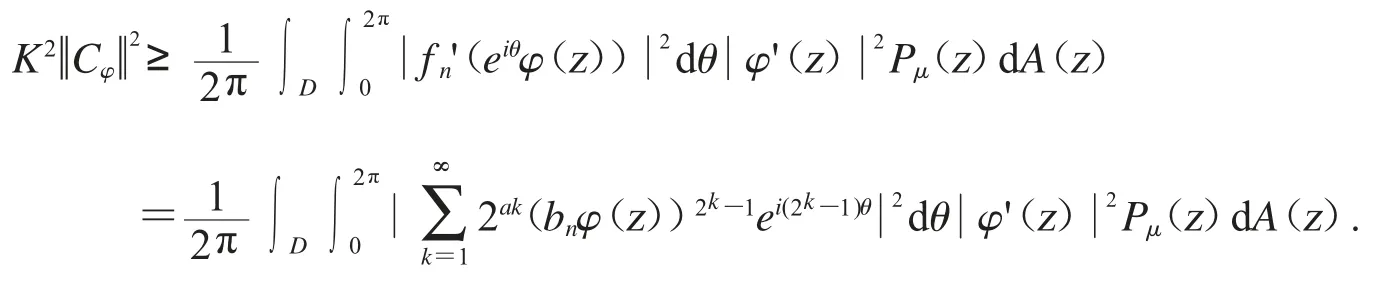
应用引理2.2 可得
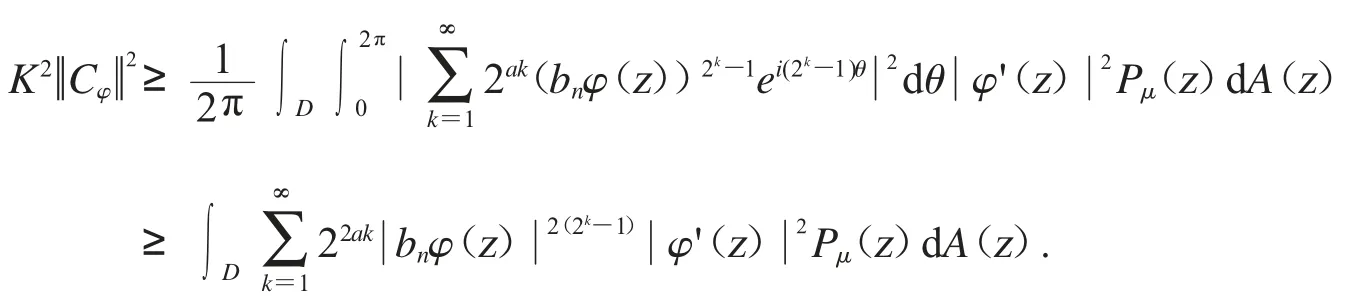
注[9]:其中对任意的r∈(0,1)和α>0 有
所以我们可得
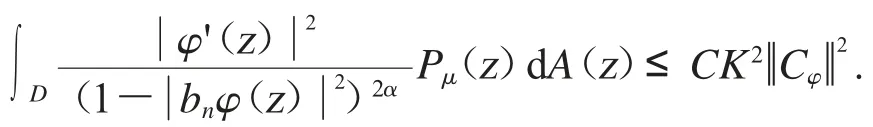
应用Fatou’s 引理可得
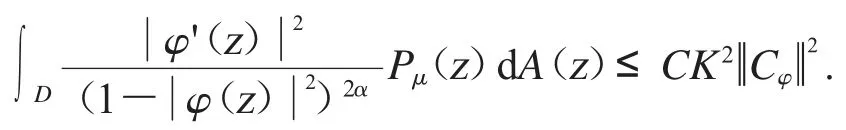
从而由(2)推导得(3).
引理2.4 设φ 是单位圆盘D 上的解析自映射.那么Cφ:Bα→D(μ)是一个紧算子当且仅当Cφ:Bα→D(μ)是有界的,且对于Bα中的任意有界序列{fn},若{fn}在单位圆盘D的任意紧子集上,当n→∞时一致收敛到0,有
证明类似于[1]中的命题3.11,在此省略证明.
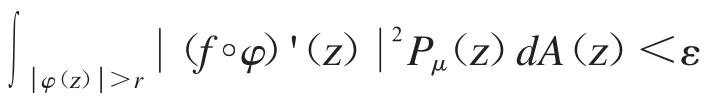
成立,其中0<δ<1.
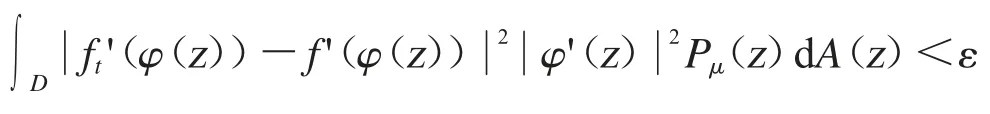
成立.对任意的r∈(0,1)应用三角不等式,可得
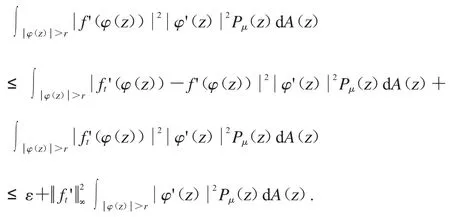
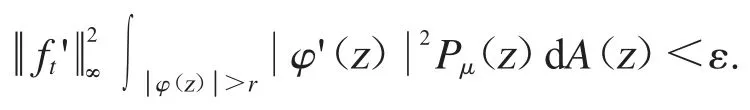
设fn(z)=nα-1zn.我们可知在D 的紧子集上一致收敛到0.因为Cφ是紧算子,我们可得因此,对任意的ε>0 和存在一个整数N>1,使得对任意n>N 时有
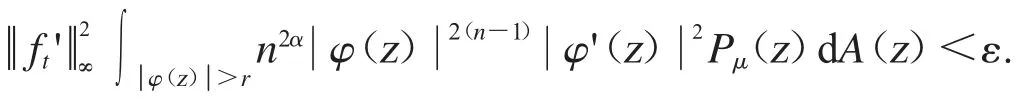
给定r∈(0,1),从上面的公式可得

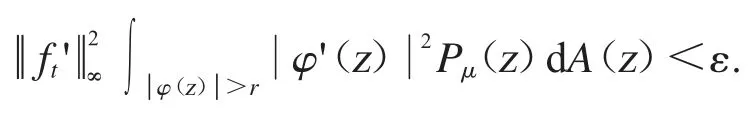
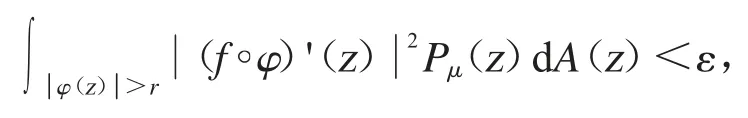
其中δ<r<1.
我们完成命题的证明是通过证得δ=δ(ε,f)是和f∈BBα0无关的.因为Cφ是紧的,Cφ在D(μ)中是相对紧的.因此,存在使得对任意的ε>0,我们可以选择fi(1≤i≤n)满足
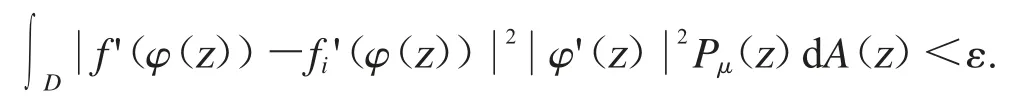
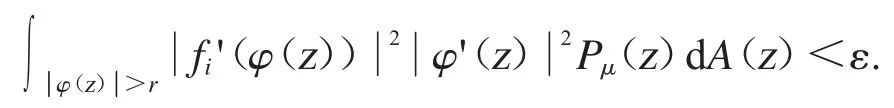
应用三角不等式可得
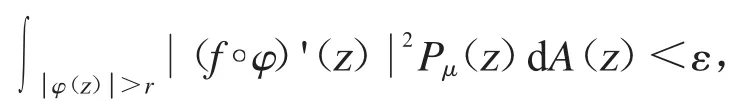
其中δ<r<1.所以命题2.5 证明完毕.
定理2.6 设φ 为单位圆盘D 上的解析自映射.那么如下叙述彼此等价:
(1)Cφ:Bα→D(μ)是紧算子;
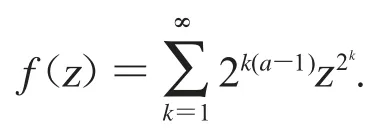
从引理2.1 可知f(z)∈Bα.设在D 上选取一个序列{an},且当n→∞时,有对所有的n∈N,设gn(z)=g(anz).对设gn,θ(z)=gn(eiθz).我们可以很容易知道gn,θ(z)∈BBα0,用gn,θ去代替命题2.6 中的函数f 和对dθ 进行积分,应用引理2.2 和Fubini’s 定理,可得
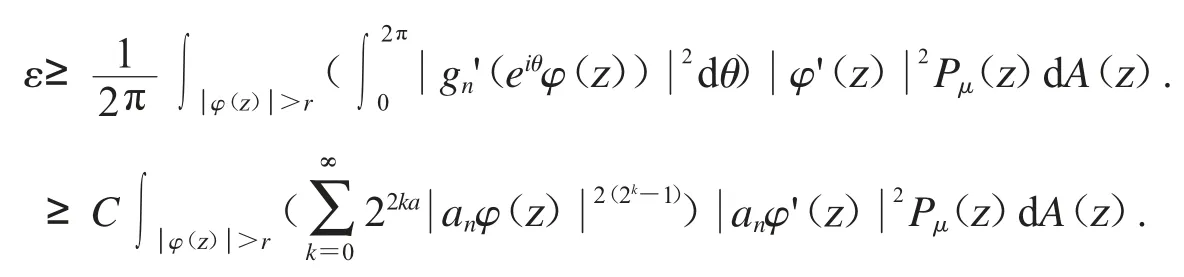
从文献[9]或[10]中,我们可以知道
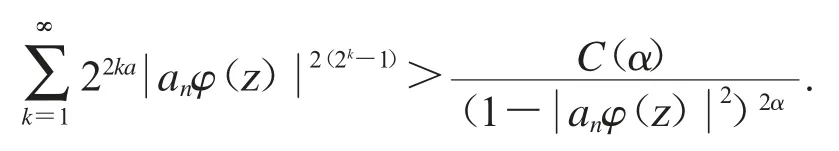
其中C(α)是只跟α 有关的常数.因此,对于充分大的n 和δ<r<1,可得
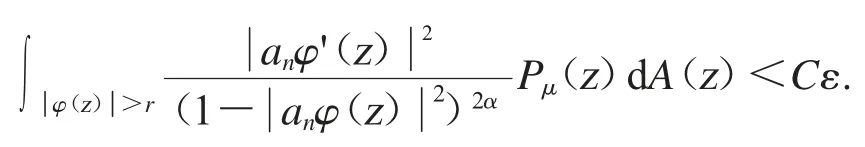
应用Fatou’s 引理,可得
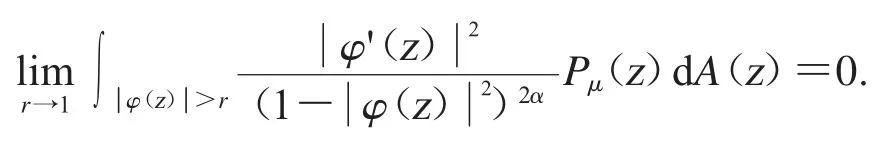
从而证明了由(2)推导出(3).
现在我们证明(3)推出(1).假设条件(3)成立,我们可以很容易检验Cφ:Bα→D(μ)是有界的.设我们只需要证明在D(μ)中有收敛的序列.设{fn}在D 的紧子集上一致收敛到0 和我们可以知道在D 的紧子集上也是一致收敛到0.如果我们可以证明那么我们将完全证明复合算子Cφ是紧算子.因为条件(3)成立,对于ε∈(0,1)所以存在r∈(0,1)使得对所有的函数fn有
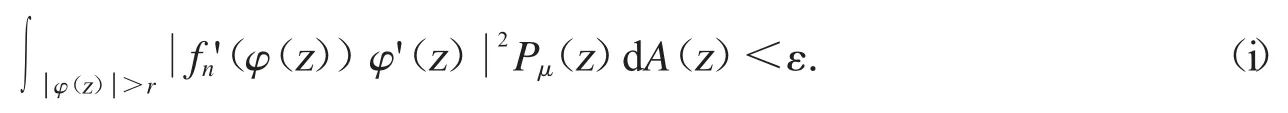
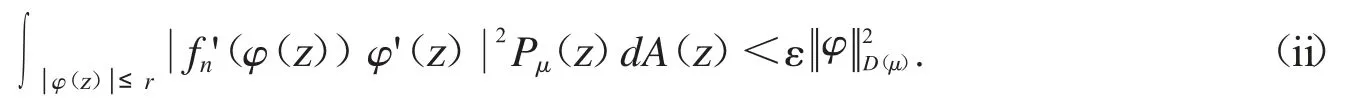
联合(i)和(ii)式.当n>N 时,可得
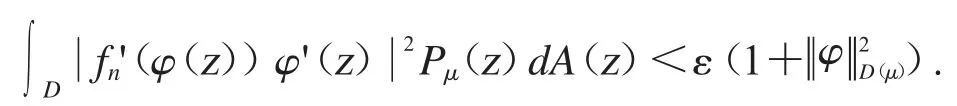
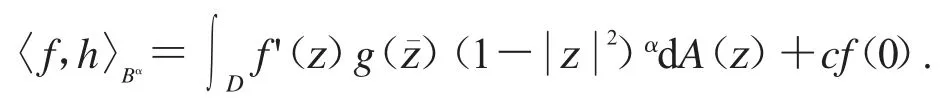
式子成立.

特别地,复合算子Cφ是紧算子,当且仅当
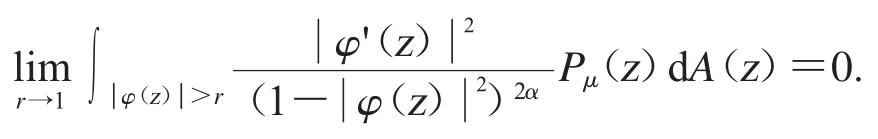
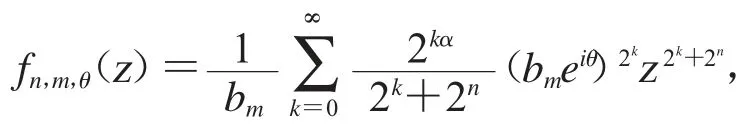
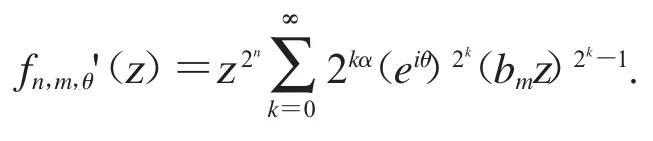
因为
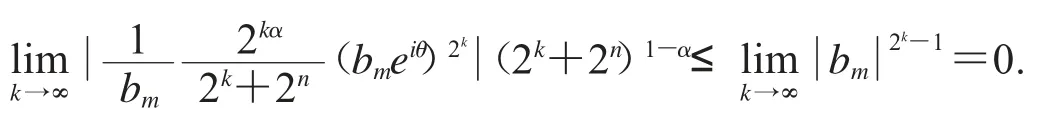
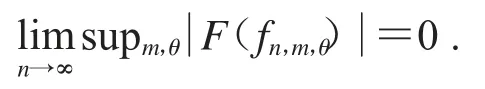
在此,如果S:Bα→D(μ)是任意的紧算子,可得
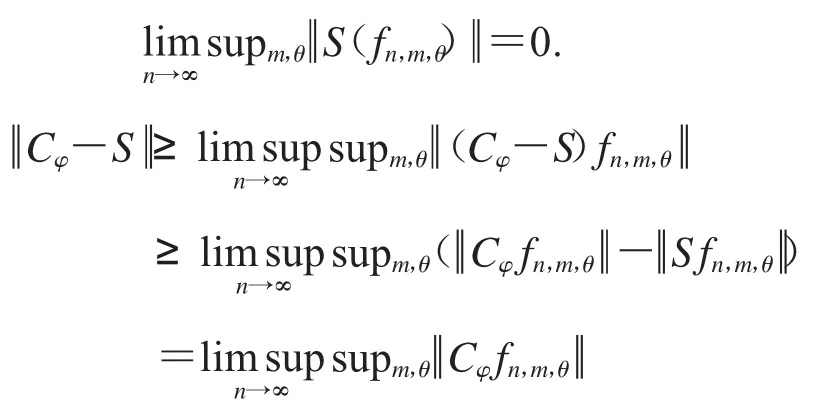
给定ε>0 存在N∈N 使得n≥N 时有
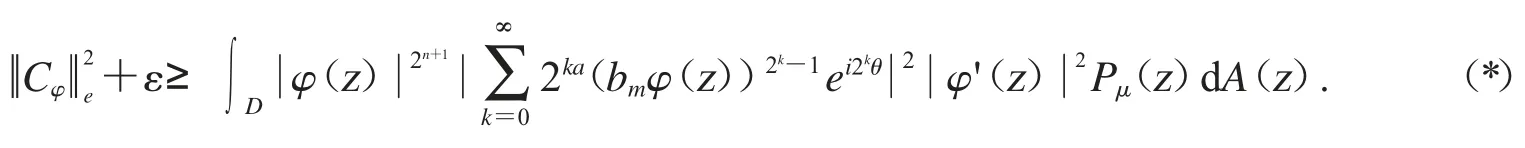
从文献[7]中,我们可以知道对所有的z∈D 如果n 和m 充分大,时.
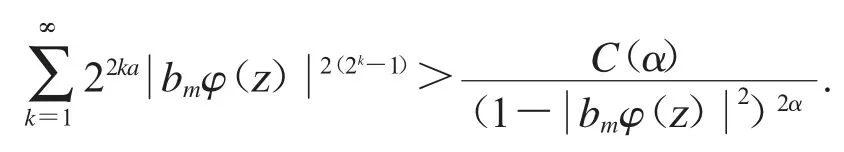
在(*)式上,两边都对θ 进行积分,应用Fubini’s 定理和引理2.2 可得
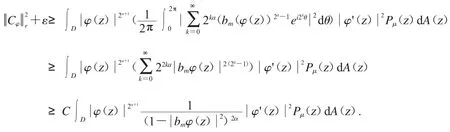
因此,应用Fatou’s 引理可得
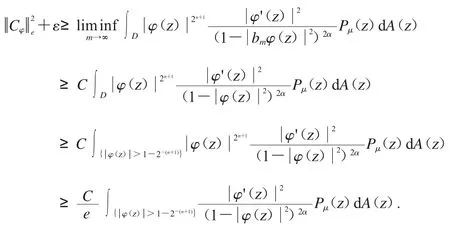
从而可得
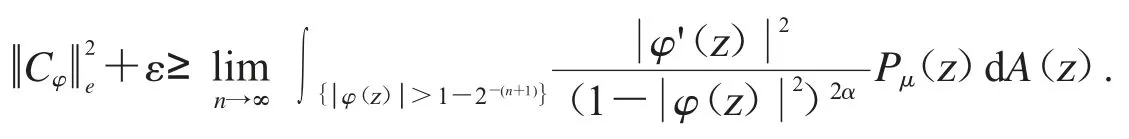
因此可得
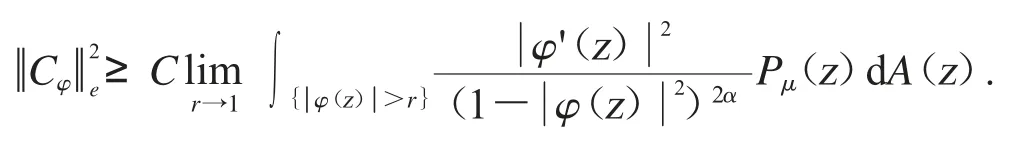
所以我们证明了下界估计.
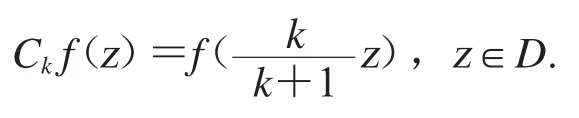
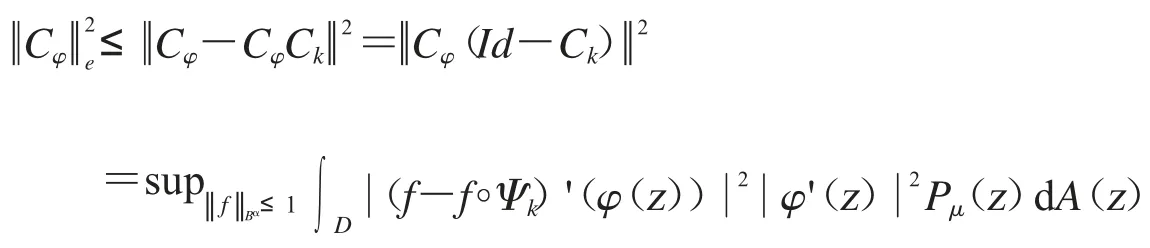
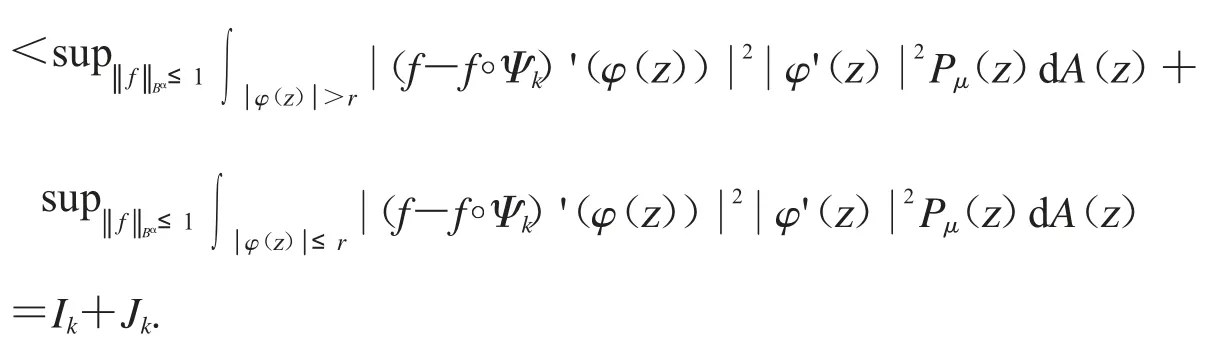
其中固定r∈(0,1).先估计第一项Ik.设和z∈D 可得
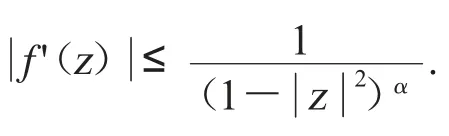
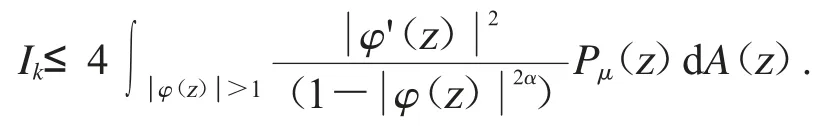
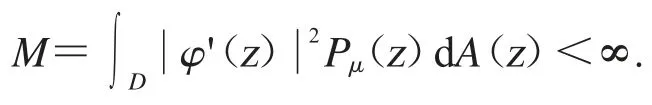
因此
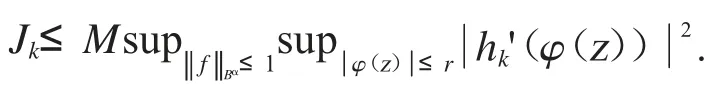
因为hk在D 的紧子集上一致收敛于0,所以我们可知hk'在D 的紧子集上也一致收敛于0.因此可得
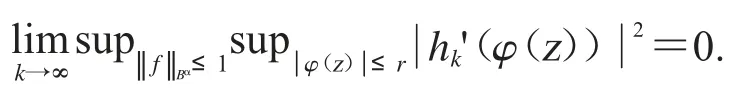
综上可得

定理证明完毕.

