基于一种新的二维混沌映射的自适应图像加密算法
黎桠娟,叶瑞松
(汕头大学数学系,广东 汕头 515063)
0 引言
随着网络技术和多媒体的快速发展,网络传输和交流变得越来越重要,并且图像在网络中的分享与传输变得越来越流行.因此,信息安全问题成了一个紧要的问题,由于数据容量大、冗余度高、相邻像素之间的相关性强,传统的加密算法如DES 和AES 已经不适用于图像加密[1-2],因此许多研究者开始寻求一种既高效又安全的图像加密算法,1989年,Matthews 首次提出基于混沌系统的加密方案[3].1997年,Fridrich 将混沌映射应用到图像加密系统[4].1998年,Fridrich 利用2D 混沌系统提出置乱-扩散结构的图像加密方案[5],在这种结构下,为了减少相邻像素之间的强相关性,首先在置换过程中对像素位置进行扰乱.之后,在扩散过程中像素值逐一改变,后一个值与前一个值相关,前后扩散两轮,类似雪崩效应.现有的图像加密算法中,此结构占据很大部分[6-10].
为了提高图像安全,研究者提出了许多有效的加密系统,如DNA 加密[10-11],混合图像加密[12],利用小波,卷积变换等加密算法[13-14]等等,在这些算法中,混沌序列的应用最为广泛[9-13,15-17],这归功于混沌映射的一些固有性质如对初始值敏感,不可预测性,以及周期性,这些性质恰好能在图像加密中得到较好的应用[4].下面将介绍一些应用混沌映射加密的算法.文献[14],第一次提出将图像滤波应用在图像加密算法中,它是基于图像块的置乱和图像滤波扩散的算法,最后的性能分析显示其加密效果很好.文献[15],基于级联调制耦合(CMC)模型提出一种新的2D Logistic ICMIC 耦合映射(2D-LICM),比起参数较少,轨道相对而言较简单的一维混沌映射,它的效果会更加优良[16].文献[10],提出自适应性DNA 随机加密算法,一般而言传统的DNA 加密算法,它的DNA 编码规则是固定的,因此可能会泄露明文信息,让攻击者有机可乘,而本文采用的是动态编码规则,即DNA 编码规则是由独立的随机序列控制.本文的性能分析显示,算法具有较高的安全性.文献[17],利用块图加密,首先将原图切分成很多子块,先对子块分别加密,再组合,与之相似的有文献[12],[12]的不同之处在于它是读入很多个原图,将这些原图,均分成子块,对这些子块全部混合加密,输出一系列密图.文献[18],提出在位平面上加密,将位平面分割成多个3D 小方块,用Chua 系统产生置乱过程的密钥,将密钥应用于3D 布朗运动中,然后对位平面的3D 小方块进行加密,复杂度比较高.
本文设计了一种新的二维混沌映射,通过对它的Lyapunov 指数曲线变化图,分岔图以及时间序列进行分析,可以看出它表现出较好的混沌性能,然后将此二维映射应用在自适应性图像加密算法中.在置乱阶段,仅改变图像像素的位置,并在此阶段计算出图像的特征,将此特征应用在扩散阶段,因此,不同的原图将为扩散算法产生不同的特征,达到拥有更强的抵抗选择明文或已知明文攻击的能力.
余下的部分由以下几个章节组成,第一节,主要介绍了新混沌映射的构造.第二节,重点分析了新映射的动力学性能,第三节,介绍了基于新混沌映射的自适应性图像加密算法,第四节,对本文提出的加密算法进行了相关的性能分析,如密钥分析、敏感性分析、统计分析等等,第五节给出全文的总结,基于所有仿真实验分析,本文所提出的算法,在数字图像加密中具有较好的性能.
1 构造新的混沌映射
考虑动力系统{R2;f},其中f:R2→R2定义为
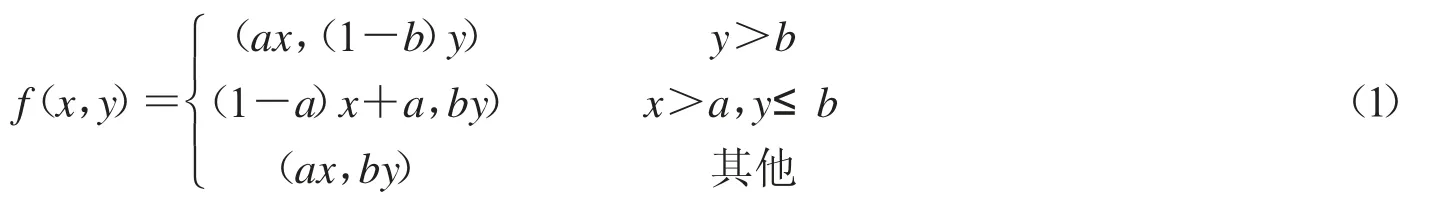
该动力系统与迭代函数系统IFS{R2;W1,W2,W3}有关,其中

当a=0.5,b=0.5 时,此迭代函数系统的吸引子就是顶点在(0,0),(0,1),(1,0)的Sierspinski 三角形(如图1),而这个动力系统{R2;f}和IFS 之间的联系就是伴随迭代函数系统IFS 的位移动力系统{Δ;f},其中Δ 表示Sierspinski 三角形,于是可将f(x,y)重写为
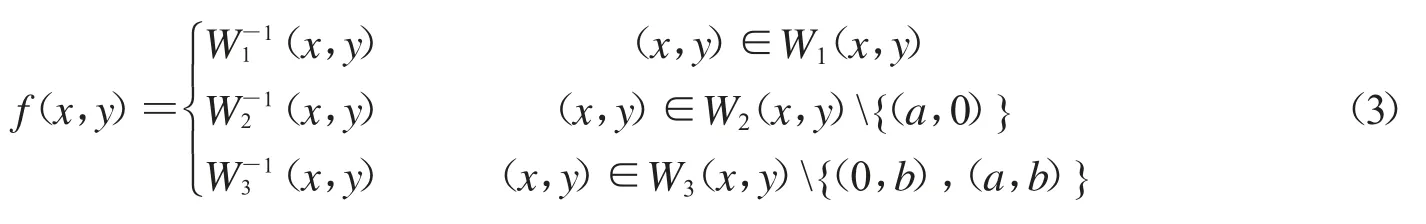
f(x,y)将Δ 映射到自身,{R2;f}是{Δ;f}的扩展.再将f 离散化,拓展为:[0,1]2→[0,1]2,具体如公式(4)所示,其中a∈(0,1),b>0.
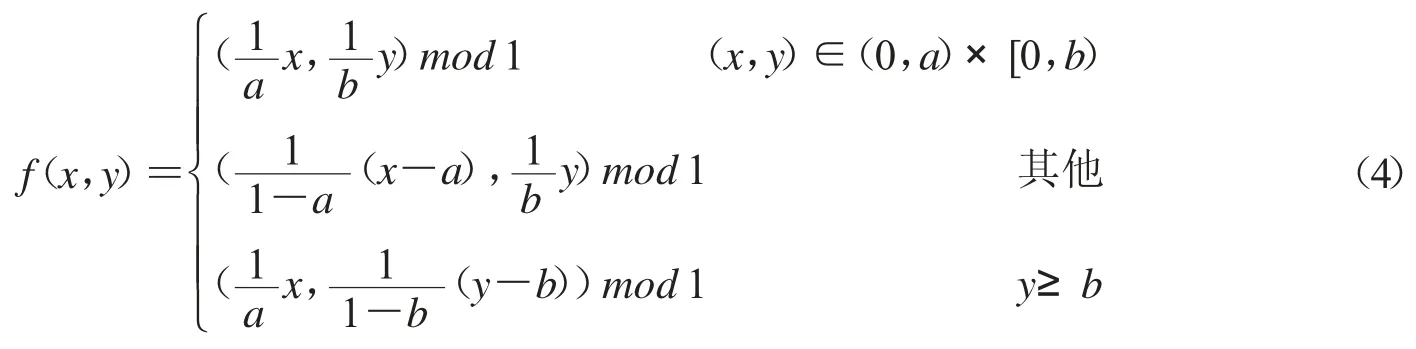
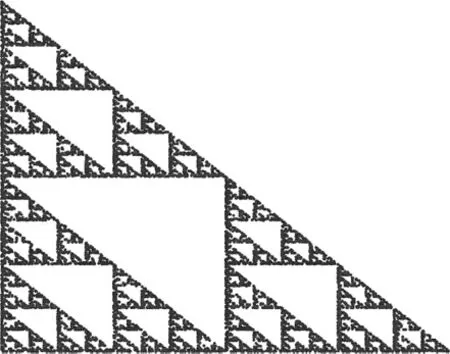
图1 Sierspinski 三角形
2 映射f的性能分析
本节将对新构造的映射(4)进行动力学性质分析,包括Lyapunov 指数曲线变化图,它的分岔图以及时间序列分析.
图2 是f 的Lyapunov 指数变化曲线图,通过取定初始值和参数b,控制a 的变化得到相应的Lyapunov 指数图,从图中可以看出在a∈[0.45,1]时,f 的Lyapunov 指数均大于0,从而可以说明本文提出的f 的结构在参数区间上是混沌的.
一个混沌系统的分岔图可以直观地观察到其动力学行为演化的过程,图3 画出了f 的分岔图,可以看出它几乎充满整个相平面,从而说明混沌性能优良,产生的序列很难被预测,这对于图像加密算法而言,是比较有利的.
时间序列分析是对混沌系统产生的时间序列进行统计分析,用统计的方法进行研究分析,寻找其变化规律,从而判断对未来的情况进行预测、决策和控制的可能性大小.为了更进一步说明映射f 所产生的混沌序列具有较好的随机性质和不可预测性,本文测试了映射f 产生时间序列的相关性,其中自相关性系数和互相关系数是两个主要的度量指数[11].对于两个随机时间序列x={x(0),x(1),x(2),…,x(N-1)},y={y(0),y(1),y(2),…,y(N-1)},它们延迟k 阶的互相关性系数(crosscorr)和延迟k 阶的自相关系数(autocorr)的数学公式定义分别如下:
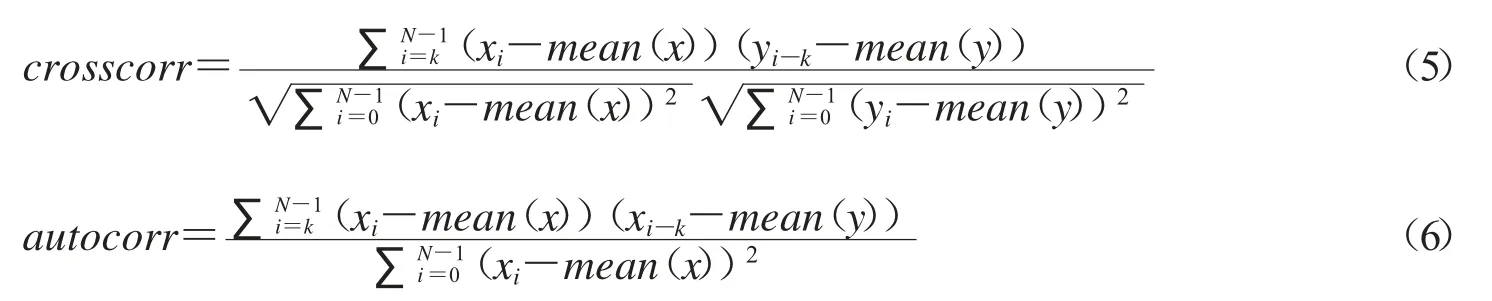
mean(x)是序列x的算术平均值.图4 是映射f 两个变量的伪随机序列变化图,图5是映射f 产生伪随机序列的自相关性和互相关性测试结果.从测试结果可以看到,混沌序列的自相关和互相关性均在0 上下波动,这说明映射f 产生的序列具有很强的随机性,因而具有不可预测性等好的密码特性,特别适合用于设计加密算法.
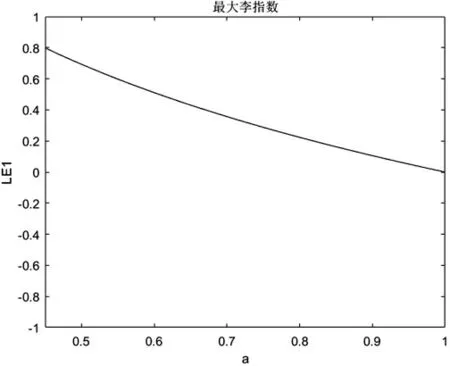
图2 f的Lyapunov 指数变化图
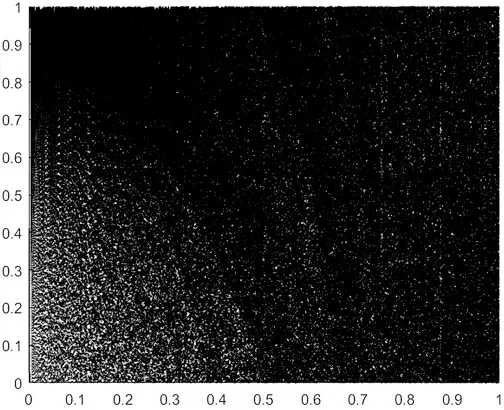
图3 f的分岔图
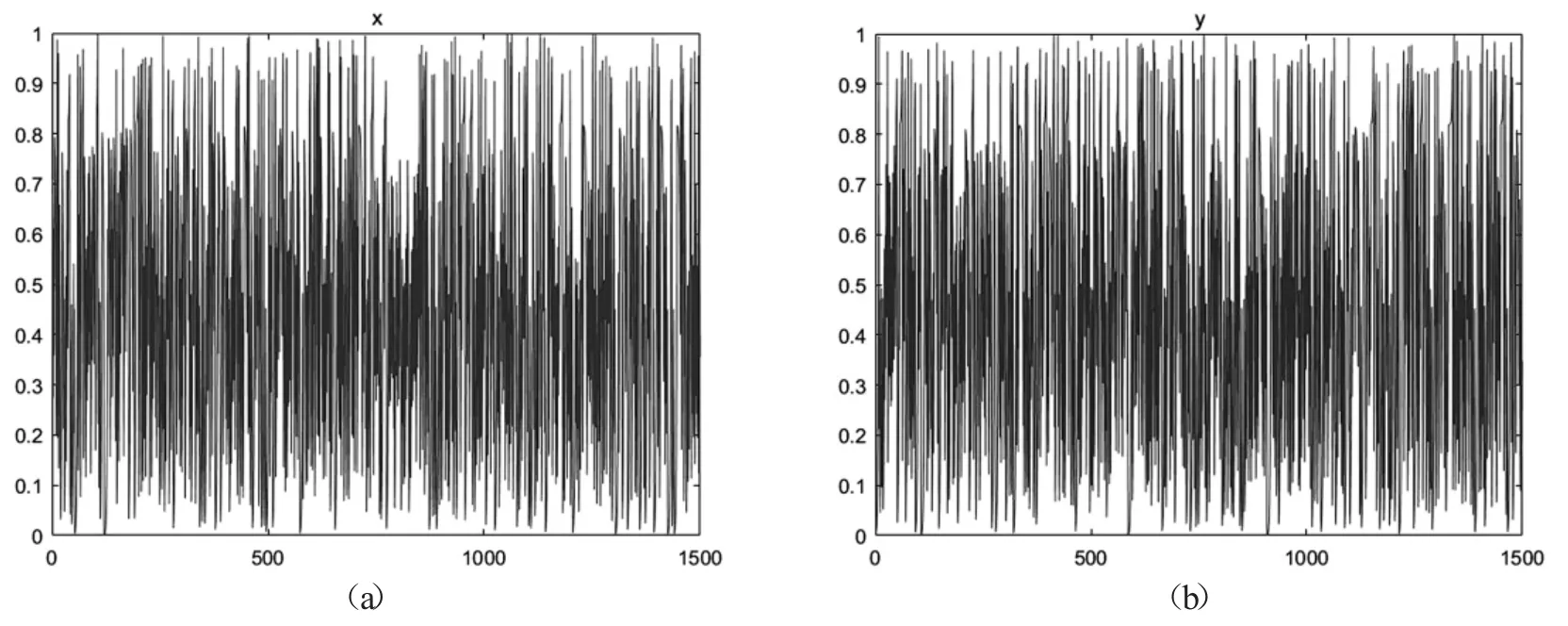
图4 (a)-(b)分别是映射f的x,y 时间序列变化图.
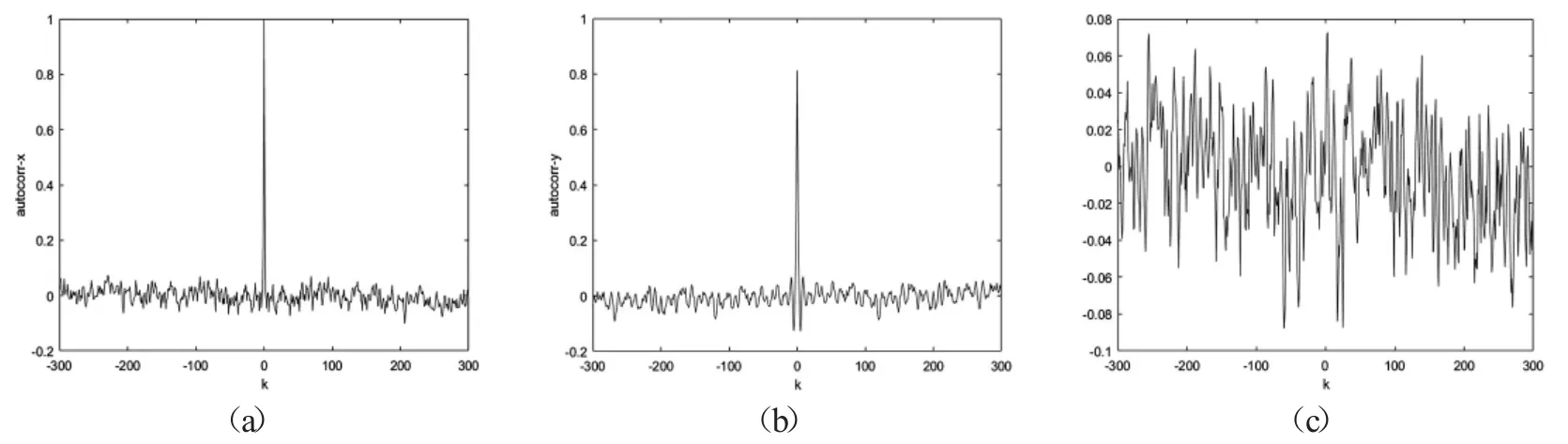
图5 (a)-(c)分别为映射f 时间序列的自相关性和互相关性测试结果.
3 系统结构
图6 为整个系统的加密过程.首先,输入明文p,混沌系统f的两套参数a1=0.45,b1=0.8,a2=0.651,b2=0.78 和初始值x0=0.454 272 34,y0=0.625 128 33,然后计算明文p的特征:
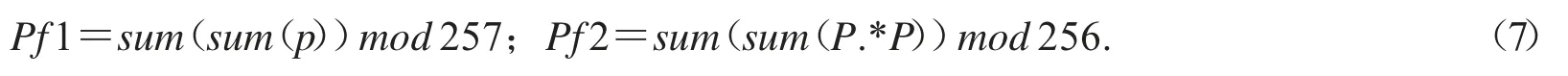
并更新初始值和参数值:
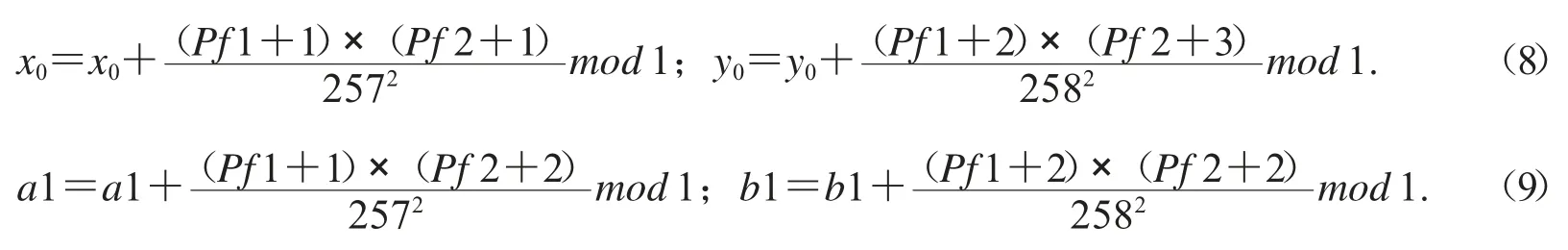
再对混沌系统f 进行迭代,迭代所产生的序列即与明文相关,最后对图像进行置乱-扩散操作,详细的加密过程展现在算法1 中.
4 仿真实验和性能分析
我们采用MatlabR2016a 对本文提出的图像加密算法进行仿真实验,本文实验图像均来自于文献[13]提到的图像数据库,我们分别对Boat,Man,Elaine 用本文提出的算法进行加密,它们的图像尺寸均为512×512,密钥分别采用x0=0.454 272 34,y0=0.625 128 33,a1=0.45,b1=0.8,a2=0.651,b2=0.78,K=1 000.其实验结果如图7,从解密加密图中可以看出,所有密文呈现杂乱无章且无明显纹理,直观上说明我们的算法加密效果可行.
算法1:图像加密
输入:明文P,混沌系统f 初始值x0=0.454 272 34,y0=0.625 128 33,和参数a1=0.45,b1=0.8;a2=0.651,b2=0.78,参数K,iter=100 000
输出:密图C
1.按(7)~(9)更新初始值,和参数a1,b1;
2.系统f 迭代iter 次,得到序列x1,iter,y1,iter,然后从x,y 分别取M,N 个值,为了避免瞬态效应,应丢弃前K 个值,即x=x(K:K+M-1),y=y(K:K+N-1);
3.计算移位参数L=floor(sum(x)×105)mod 256,并将x,y 按升序排序,根据值在原始x,y 中的位置可以得到下标向量X,Y;
4.初始化矩阵BM,N,DM,N,CM,N,M,N 表示矩阵的大小;
5.for i=1:M
6.for j=1:N
7.B(i,j)=P(X(i),Y(j));置乱图像像素位置;
8.if j-L≥1
9.D(i,j-L)=B(i,j);移位
10.else
11.D(i,j-L+N)=B(i,j);
12.end
13.end
14.end
15.利用更新前的初始值x0,y0和a2,b2 再对系统f 迭代iter 次,得到序列x1,y1;
16.取x1=x1(K:K+M*N-1),y1=y1(K:K+M*N-1),并且得到X1:x1=reahspe(x1,M,N),X1=floor(x1×1014)mod 256,floor 表示向下取整,mod 表示取余,sum 表示求和;
17.扩散算法:
18.C(i,j)=D(1,1)+X1(1,1)+sumx1+sumy1mod 256;
19.for j=2:N
20.C(1,j)=D(1,j)+X1(1,j)+C(1,j-1)mod 256;
21.end
22.for i=2:M;
23.C(i,1)=D(i,1)+X1(i,1)+C(i-1,1)mod 256;
24.end
25.for i=2: M
26.for j=2:N
27.C(i,j)=D(i,j)+X1(i,j)+C(i-1,j)+C(i,j-1)mod 256
28.end
29.end
4.1 统计分析
本节将通过直方图、相邻像素之间的相关性和信息熵来评估算法抵抗统计攻击的能力[19].
4.1.1 直方图分析 图像的直方图反映了一副图像像素值的分布情况,为了对抗统计分析的强力攻击,图像的直方图最好是接近完全一致分布的,且与原图的直方图相比具有显著差异[15],图7 中的(d)~(f),(j)~(l)分别表示三幅原图像的直方图,和加密后的直方图,直观上可以看出,加密图像的直方图是接近完全一致分布的,且与原图具有显著差异,所以这个算法足够对抗统计分析的强力攻击.
4.1.2 像素间的相关性分析 一般地,数字图像具有异于文本的一些固有特性如数据的高度冗余、相邻像素的相关性非常强等,攻击者往往利用这些特性对密文图像进行攻击,所以一个理想的图像加密算法应该产生在水平、垂直、正对角方向上的相邻像素点间相关性都比较弱的密文图像[20].
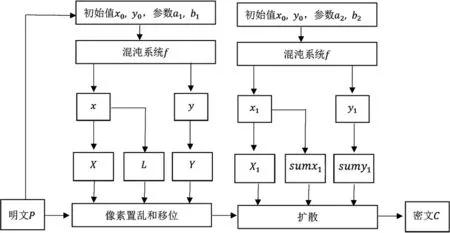
图6 图像密码系统流程图
设从需要考察的图像中任取N 对相邻的像素点,记它们的灰度值(ui,vi)i=1,2,…,N,则向量u={ui}和v={vi}间的相邻系数计算公式如下:
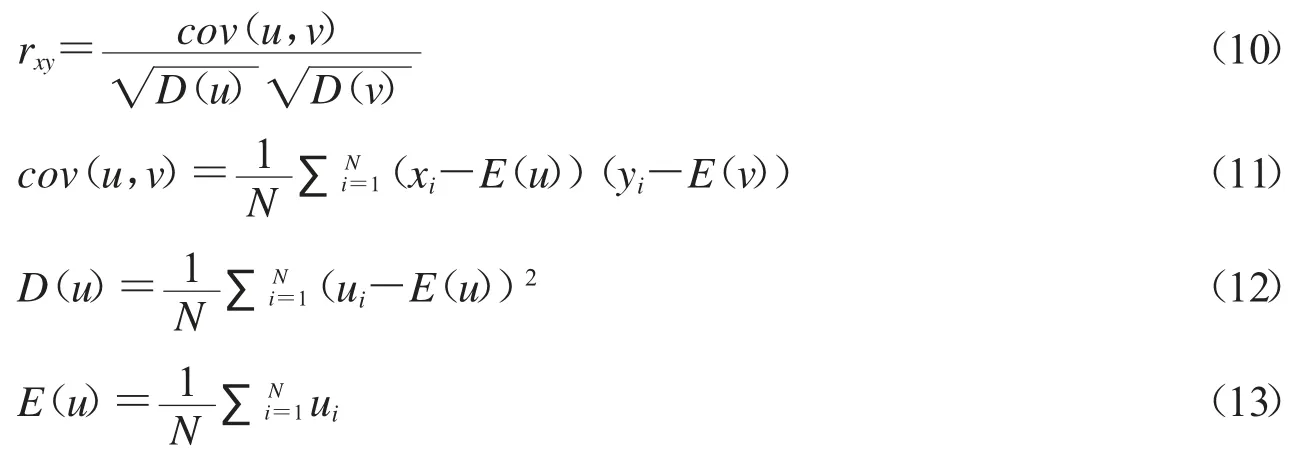
在实验分析中,我们将从明文Man 及其密图中分别随机选取5 000 对像素,分析它们在水平、垂直、对角方向的相关性,结果显示如图8,由图可知明文图像在各个方向上的相邻像素点对密集在y=x 直线上,而密文图像在各个方向上的相邻像素点对在矩阵为(255,255)区域内均匀散布着,说明明文图像在各个方向上具有颇强的相关性,而密文图像在各个方向上的相关性很弱.同时我们计算了Boat,Man,Elaine的相关性系数,结果显示在表1.
实验结果表明明文图像相邻像素点的相关性比较高,而密文图像相邻像素点的相关系数接近于0,近似无相关性(两个独立不相关的序列的相关系系数理论值为0).

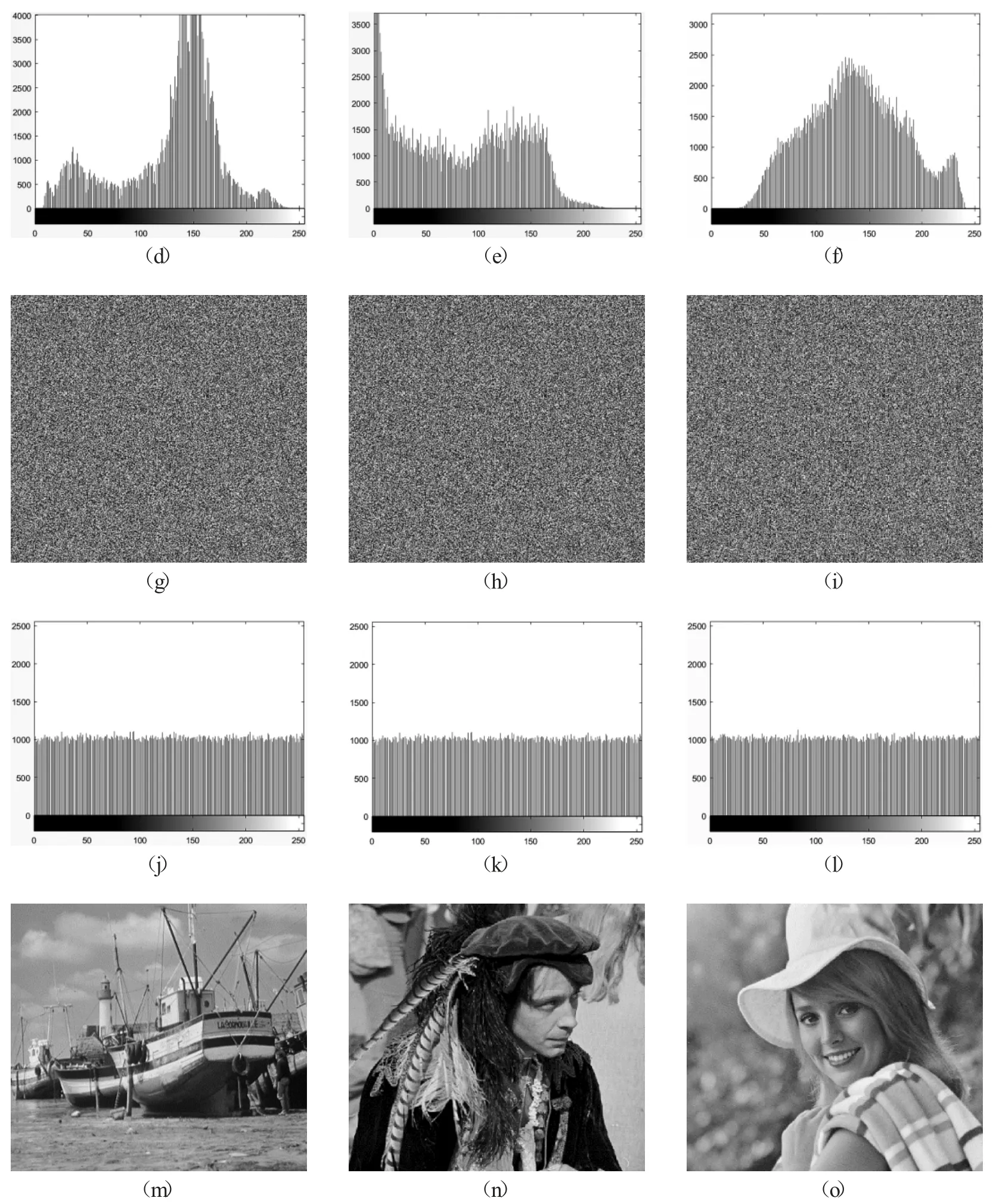
图7 (a)~(c)分别为Boat, Man, Elaine的原图;(d)~(f)是(a)~(c)的直方图;(g)~(i)是(a)~(c)的加密图;(j)~(l)是(g)~(i)的直方图;(m)~(o)是(g)~(i)的解密图;
4.1.3 图像信息熵分析 信息熵是反映一个信息源的随机性和不可预测性的数学概念.对于数字图像来说,信息熵反映了图像信息的不确定性.一副图像如果有L 种灰度值mi(i=0,1,2,…,L-1),且各灰度值出现的概率分别p(mi)(i=0,1,2,…,L-1),则根据Shannon 定理,图像的信息量为:
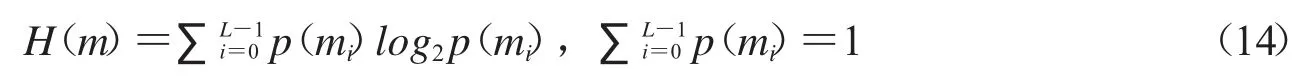
称H为图像的信息熵,当图像中各灰度值出现的概率相等时,图像的信息熵最大,信息熵表示一副图像所包含信息的多少,信息熵可以度量灰度值的分布,对于理想的随机图像,其信息熵等于8[14],本文分别计算了Boat,Man,Elaine的信息熵,及其相应密文的信息熵,实验结果如表2所示,由表2中数据可看出,各个密文图像的信息熵接近于理论值8,而各个明文图像与理论值有明显差异.
根据文献[21]提出的Local Shannon entropy(LocSE)从局部观点测试一副图像的随机性.它对不同的尺寸的图像有效且公平.从一副图像中随机选取k 个不重叠的图像块S1,S2,…,Sk,共有TB个像素,则LocSE的定义如下:

H(Si)可以利用(14)计算.根据参考文献给出的参考值,本文中取k=30,TB=1 936,α=0.05,则Hleft=7.901 901 309,Hright=7.903 037 329,计算结果显示在表3,计算得到的结果均在Hleft,Hright之间,这意味着本文提出的算法可以将各种不同的明文图像加密成随机密文图像.
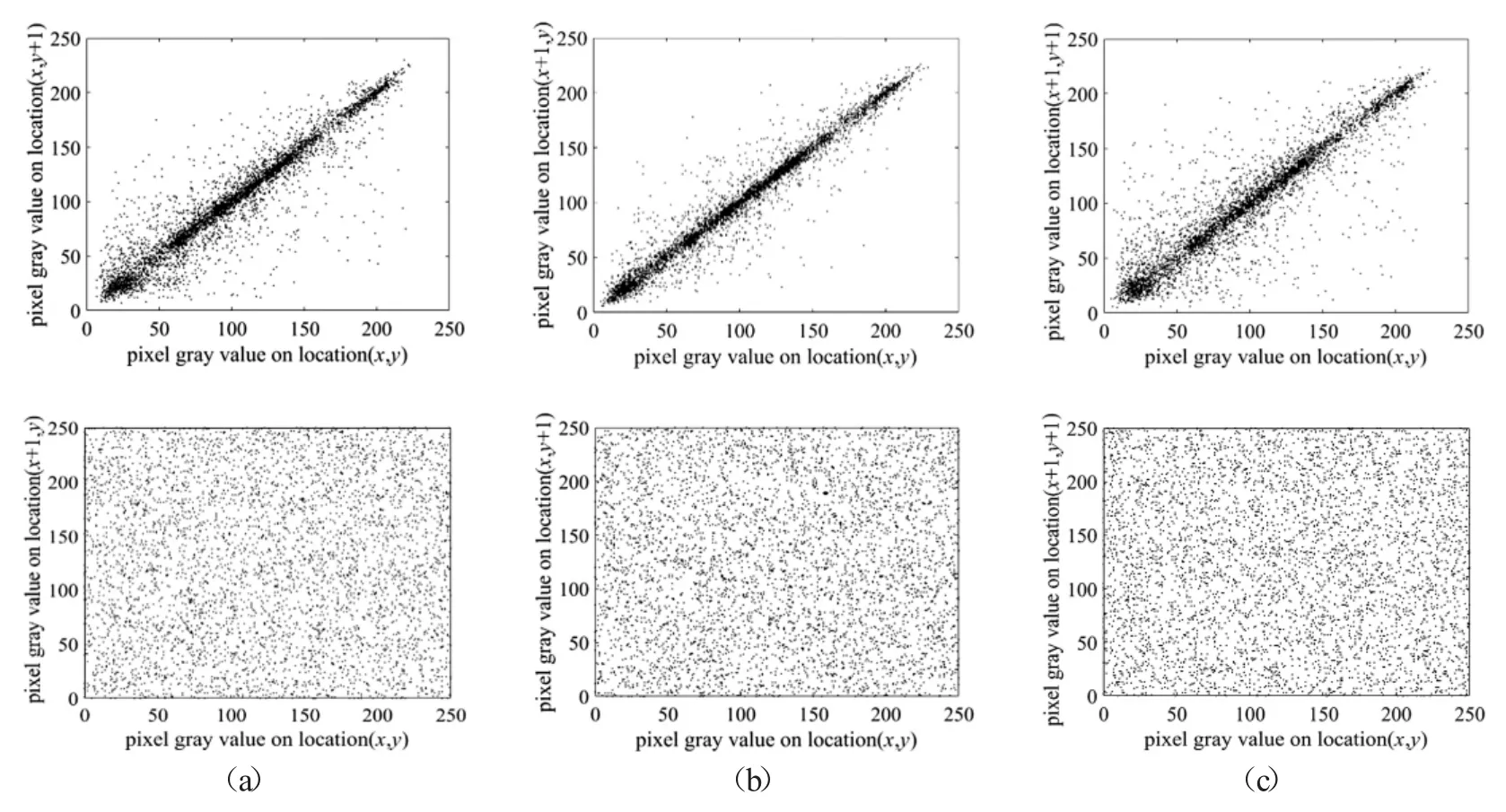
图8 (a),(b),(c)分别为明文和密文在水平、垂直和对角方向像素的分布
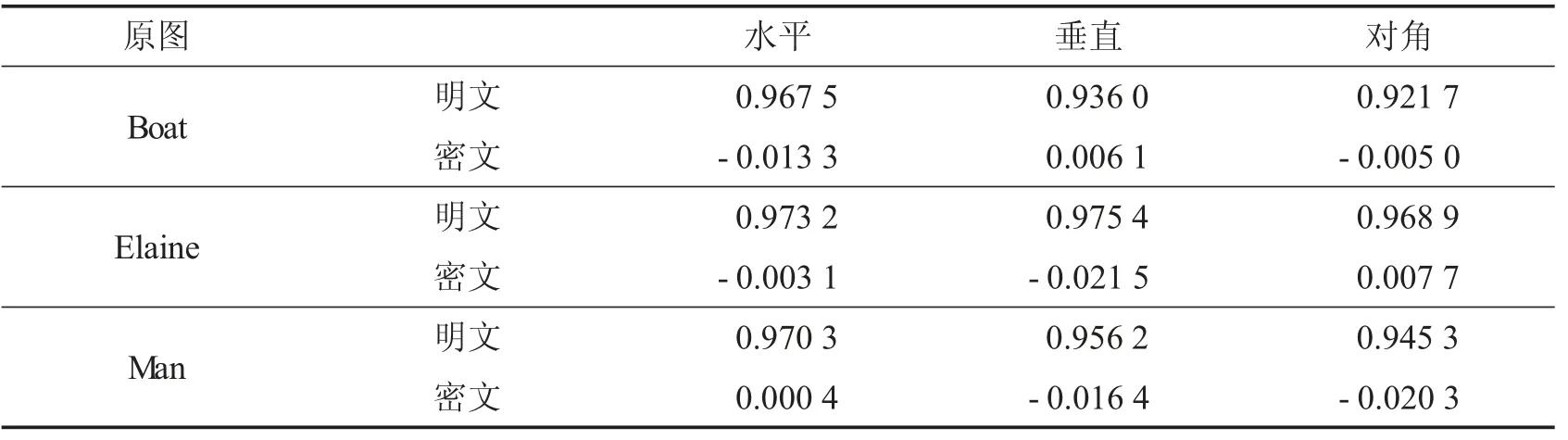
表1 明文与其密文分别在水平、垂直和对角方向上的相关系数
4.2 密钥空间
密钥空间是指所有合法密钥构成的集合,图像密码系统的密钥空间应该足够大,从而可以有效地对抗穷举攻击,特别是加密解密速度非常快的密码系统,密码长度至少应该为128b[14],本文所提出的加密算法有7 个密钥:x0,y0,a1,b1,a2,b2,K,其中x0,y0,a1,b1,a2,b2 均在0 和1 之间,设计算机精度为10-14,图像大小为512×512,K=103,则整个密钥空间至少约为这个值远远大于128b,这意味着我们的算法能够经受得住暴力破解.

表2 信息熵实验结果

表3 不同图像的LocSE 实验结果
4.3 密钥敏感性
为了保证系统的安全性,一个优良的加密系统必须对密钥极端敏感,即当使用不同的密钥对密码图像进行解密时,将得不到明文.在实验中,我们将用密钥key 去加密Man,得到密图,而用几个与key 差别极其微小的密钥去解密密图,如果系统足够敏感的话,是无法得到明文的,图9 展示了密钥敏感性测试,同时,表4 展示了用key1~key7 解密图与用key 加密的密图之间的NPCR 和UACI.



表4 用极小差别密钥解密的图片与密文的NPCR 和UACI

图9 加密敏感性测试:(a)~(f)分别为用key 和key1~key7 去解密key 所产生密文得到的明文
4.4 差分分析
在图像加密系统中,差分分析指探究在相同加密密钥的条件下,密文图像会在多大程度上受明文图像的影响,攻击者通常通过选择明文分析或选择密文分析来实现差分攻击,为了测试加密系统对明文的极端敏感性,采用两个常用的度量:不同密文图像之间的像素改变率(number of pixels change rate,NPCR)和不同密文图像之间的一致改变强度(unified averagechanging intensity,UACI),NPCR 是用来比较两幅图像相应位置的像素点的值,记录不同的像素点个数占全部像素点的比例,而UACI 则是比较两幅图像相应位置的像素点的值,记录它们的差值,然后计算全部相应位置像素点的差值与最大差值(即255)的比值的平均值.它们的数学定义如下:
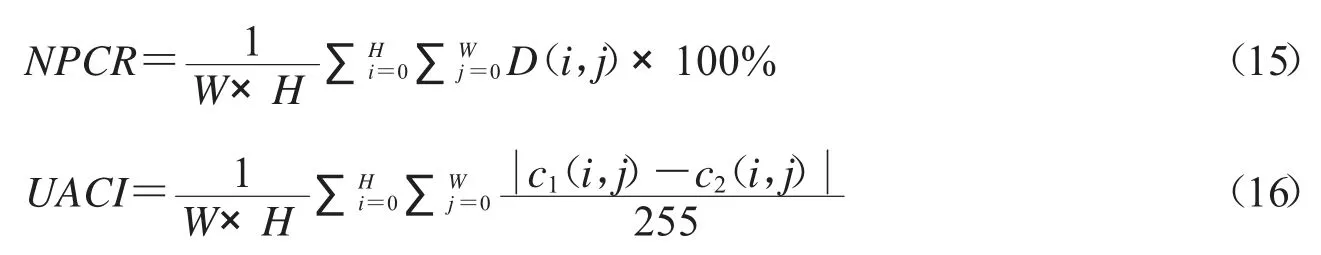
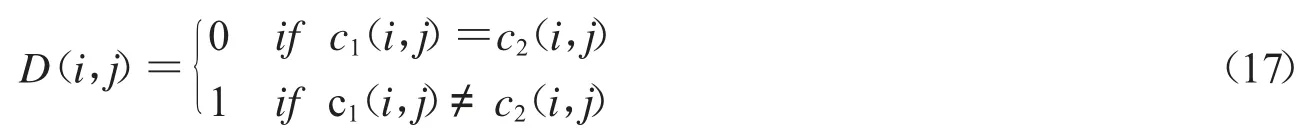
这里W,H 分别是矩阵图像的行数和列数,c1(i,j),c2(i,j)分别是对应于两副微小差别图像用同一个密钥加密的密图像素点的值.理论上来说两幅随机图像的NPCR,UACI 理论期望值分别约为99.609 4%,33.463 5%,本文将用Man 和Boat 来完成差分实验,对于每一个实验图片,将随机选取1 000 个像素点,每次改变一个像素值,得到一个新的图像,然后用同样的密钥去加密两个原图,这两个原图之间只相差一个像素值,结果呈现在表5,6 以及图10,实验结果表明,本文提出的算法所得的NPCR,UACI 值极其地接近期望值,这表明本文算法达到一个优良的扩散性能,它对原文非常敏感.所以它能够抵抗差分攻击.

表5 不同明文的NPCR

表6 不同明文的UACI
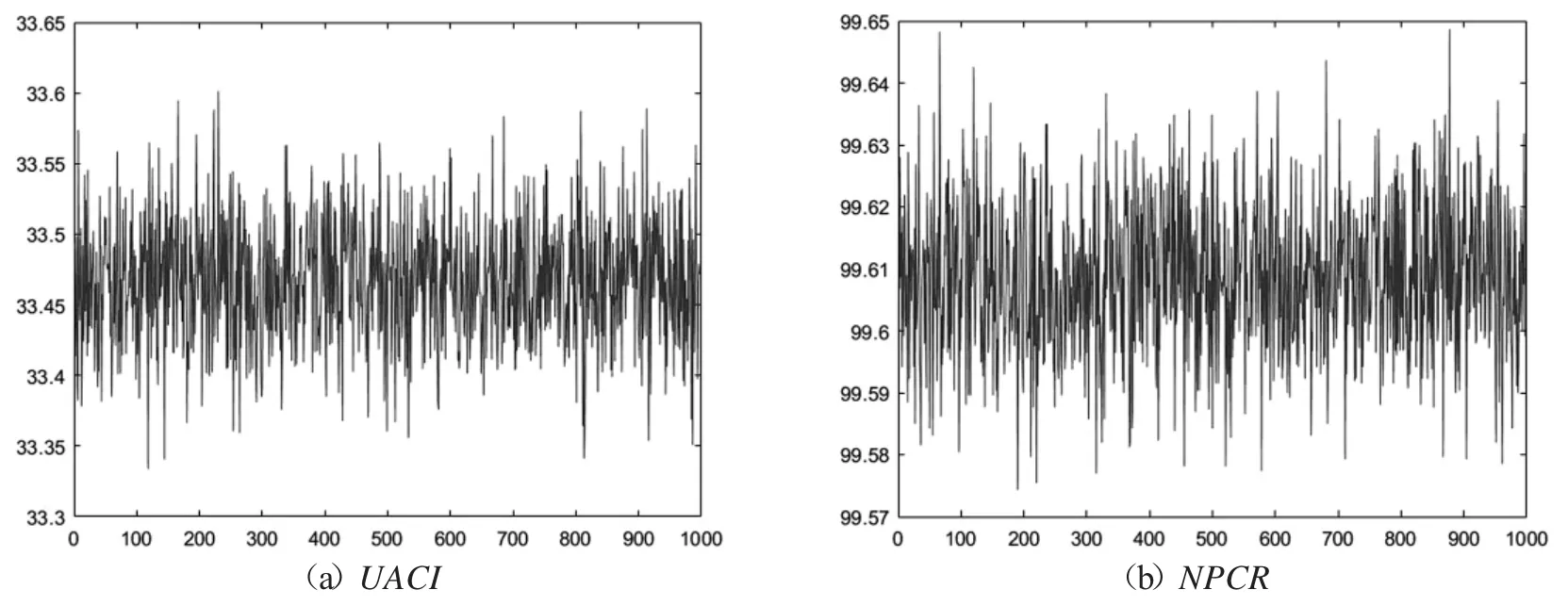
图10 只改变一个像素值的1 000 张图片的NPCR 和UICA.
5 总结
本文提出基于一种新的二维混沌映射的自适应性图像加密算法.首先本文设计了一种新的二维混沌映射,对其混沌学性质进行了全方位的分析,其展现出较好的混沌学性质,将其应用在加密算法中.然后,将本文加密算法分为置乱和扩散两部分,为了加强抵抗选择明文或已知选择明文攻击,在置乱阶段,计算出图像特征,将此特征应用在扩散阶段,从而不同的原图将为扩散算法产生不同的特征.最后有关本文提出算法的重要安全性能分析被提出,包括密钥分析、敏感性分析和统计分析等,所有的实验结果均表明,本文提出算法具有较强的鲁棒性,因而具有一定的应用价值.

