基于多特征融合的运动想象脑电信号识别研究
姜月,邹任玲
上海理工大学医疗器械与食品学院,上海200093
前言
脑机接口(Brain Computer Interface,BCI)是不依赖于大脑的正常输出通路(外周神经系统和肌肉组织),即可实现大脑与外界环境交流的一种人机交互方式,它通过对外部设备的控制使人们的意愿得到表达。BCI 系统利用采集的特定模式的脑电信号(Electroencephalogram,EEG)分析识别,转换为相应的控制命令,实现预期功能。BCI能否准确实现用户意愿,关键在于脑电识别率,直接影响着最终的控制准确度,而算法优化就是提高识别率的关键。
Gaur 等[1]采用经验模态分解(Empirical Mode Decomposition,EMD)提取频段能量等作为特征,采用线性判别分析分类,获得了70.2%的平均正确率。针对单一特征通常分类效果一般,目前很多研究开始组合使用不同特征提取方法。Peng 等[2]采用希尔伯特-黄变换(Hilbert-Huang Transform,HHT)提取自回归(Auto Regressive,AR)模型参数等作为特征,使用支持向量机(Support Vector Machine,SVM)分类,识别率达到91.65%。金海龙等[3]利用HHT提取边际谱能量差,并结合EEG时域复杂度作为特征量,使用BP神经网络分类,达到87.14%的识别率。Chatterjee等[4]提取统计特征,小波的能量、熵及均方根,功率谱密度的平均功率、频带功率共26维特征向量,分别使用SVM 和多层感知器得到85.00%和85.71%的识别准确率。将不同特征结合更好地体现了EEG的有用信息,为分类器提供更优的输入。
本研究提出利用EMD 分解EEG 得到内蕴模态函数(Intrinsic Mode Function, IMF),提取其前三阶的能量值,用共空间模式(Common Spatial Pattern,CSP)得到空域特征,求取6 阶AR 模型系数,将组合后的20 维时-频-空特征向量采用主成分分析(Principle Component Analysis,PCA)降维,新的低维特征用SVM分类,并与其它算法比较,验证本研究方法的有效性。
1 数据来源
为了客观评价算法的有效性,本研究采用BCI2003中由Graz科技大学提供的脑电数据(Data set III)。受试者为1名25岁健康女性,任务为根据屏幕的随机提示以想象左右手运动的方式控制目标左右移动。如图1所示,t=0~2 s时,受试者处于安静放松状态;t=2 s时,出现声音提示实验开始,并有“+”显示在屏幕上且保持1 s;t=3 s时,向左或向右的箭头出现,受试者想象左手或右手运动以使方块左右移动,直至9 s结束。信号采集使用差分放大器和Ag/AgCl电极,采集通道为国际标准10-20导联系统中的C3、Cz和C4这3个通道,如图2所示。其中,C3和C4位于大脑初级感觉皮层运动区,能有效反映肢体运动或想象运动时的相关节律变化,Cz位于大脑中央部位,作为参考电极。信号采样率为128 Hz,进行0.5~30.0Hz带通滤波。
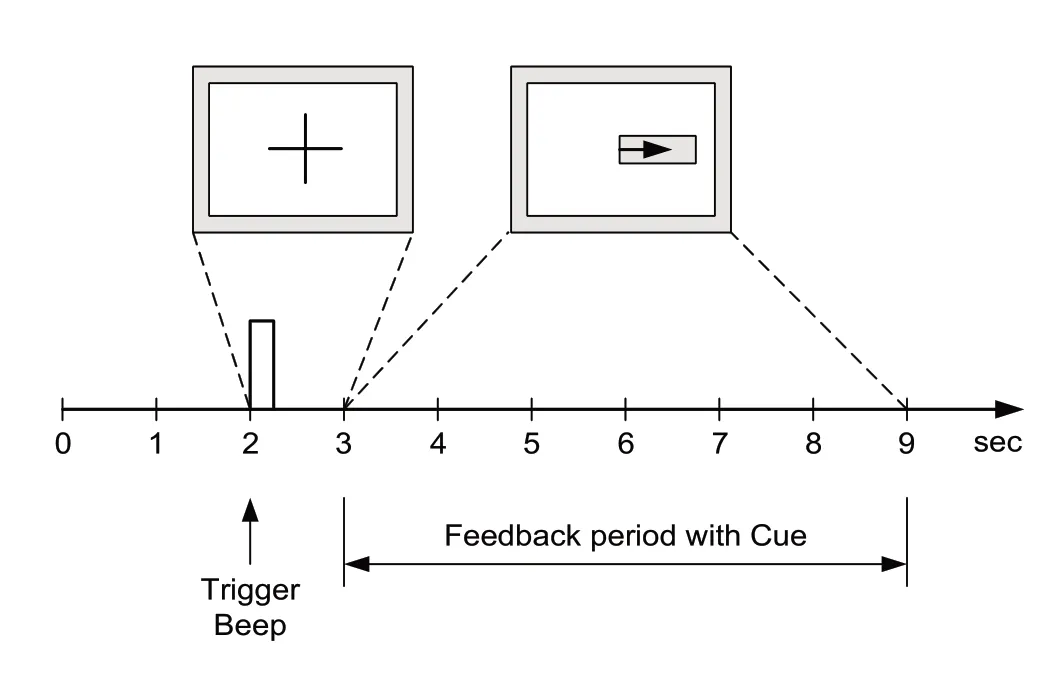
图1 实验时序示意图Fig.1 Experimental sequence diagram
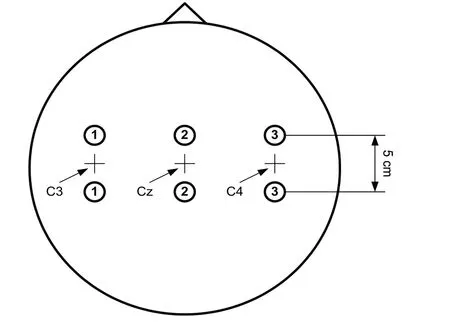
图2 电极放置位置Fig.2 Position of electrodes
2 特征提取方法
本研究采用的特征提取方法是提取3 种特征值后进行多特征融合,可以更好突出EEG 特征信息。下面将特征提取各部分算法的实现分别介绍。
2.1 EMD
EMD 是一种针对非线性、非平稳信号的时频分析方法,EEG 正是这种信号。与同为时频分析的小波变换相比,它不需要选取基函数与分解层数,具有自适应性[5]。它从信号时间尺度特征出发,进行平稳化处理,将原始信号分解成一系列不同尺度的单一分量,即IMF[6-7]。IMF 应满足两个条件:(1)在整个序列中极值点数量与过零点数量须相等或至多相差一个;(2)在任意时间点上、下包络线均值为零,即信号关于时间轴局部对称[8]。
EMD对脑电信号时间序列x(t) 的处理步骤如下:
(1)确定x(t) 的所有局部极值点,用三次样条插值函数进行拟合,由局部极大值和极小值点分别形成x(t)的上包络线m+(t)和下包络线m-(t),并计算两包络线的均值为:

(3)计算x(t)减去c1(t)后的残差r1(t),将r1(t)作为新序列,重复步骤(1)和步骤(2),可依次得到第二阶、第三阶IMF分量等,即c2(t),c3(t),…,cn(t),直至rn(t)为单调函数且无法继续从中提取分量,分解则结束。此时,可将x(t)表示为所有IMF 分量和残差之和,即:

其中,n为得到的IMF个数。
EEG信号被分解成一系列IMF后,突出了不同时间尺度的局部特征,且随阶数增大所代表的频率逐渐降低。一般分解EEG后的IMF数目为5~8个[9],但并非所有都包含重要信息,只需选择部分IMF即可。
2.2 CSP
CSP主要针对二分类问题,非常适合左右手运动想象的特征构造,其基本原理是对两个协方差矩阵同时对角化,并提取两种任务的空间成分,构建两类空间滤波器,使两类差异最大化[10]。实现步骤如下:
(1)分别计算两类信号的协方差矩阵:

其中,Ei表示想象左手和右手的数据矩阵,为迹,表示矩阵对角线元素之和。

(4)进行白化处理,构建白化矩阵P:

利用P 使Ci变成如下形式:
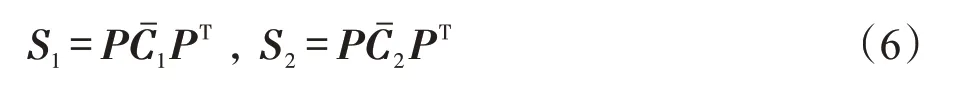
(5)由于S1和S2具有相同特征向量,再次特征值分解,得到:

其中,B 为两者共同的特征向量,且λ1+λ2=I(I 为单位矩阵),也就是当其中一类特征值最大时,另一类特征值必为最小。
(6)按照特征值大小将对应特征向量从大到小排序,取前m 个特征向量组成矩阵B1,其余为B2,则构成一对空间滤波器分别为:

利用它对EEG 矩阵Ei滤波,则Ei被变换为Zi=Wi×Ei。
(7)将Zi作如下运算作为特征值:

其中,p=1,2,…,2m(2 m <n)。将所有fp构成最终特征值矩阵F={f1,f2,…,f2m} ,即为一组脑电特征[11-12]。
2.3 AR模型
AR 模型属于时域分析,基本思想是:假设可用自回归过程近似于真实的EEG,从而可用较少的参数反映较多谱信息[13]。基于此假设,选取合适的阶次和参数,可使AR 过程最大程度逼近EEG。AR 模型的参数辨识简单,实时性较好,因此AR 系数作为脑电特征量非常合适[14]。
对于一般随机信号,AR模型可以表示为如下形式:
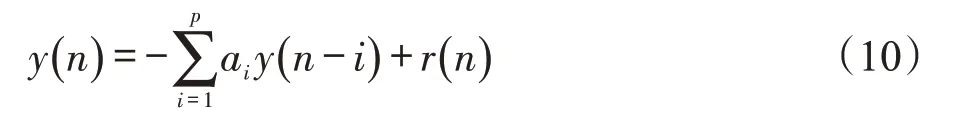
其中,y(n)是信号的第n 个采样值,p 是模型阶数,{ai} 是模型系数,r(n)为零均值白噪声的残差。本研究运用Burg算法进行系数估计,主要原理如下:
令ep(n)和bp(n)分别为AR模型的前向和后向预测误差,Pe和Pb分别为它们的功率,具体表达式这里不进行赘述。令两功率之和为:

当阶数i=1~p 时,ei(n)与bi(n)有如下递推关系:
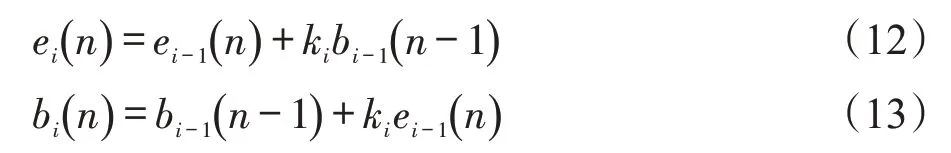
其中,e0(n)=b0(n)=y(n),ki为反射系数,ki=aii。
Burg 算法的目的是使Peb相对于ki最小。系数ai则可由Levinson-Durbin递推算法求出:

选择阶数是影响AR系数特征的关键,本研究选择的阶数为6。
2.4 基于PCA的特征降维
上述3种算法得到的特征向量组合后维数较高,不利于分类器识别,使算法不够准确快速,因此选择PCA 算法实现降维。PCA 根据方差最大化原理,用一组线性无关且相互正交的新向量来对原向量进行表征,这组新向量即主成分,是原来向量的线性组合[9]。实现步骤如下[15-16]:
(1)设原始特征集为{x1,x2,…,xn},先进行去均值处理,得到中心化后的矩阵:

(2)计算X 的协方差矩阵C,C=XXT。对C 特征值分解,C=UλUT,得到特征值λ 和特征向量U ,λ 为对角阵,表示主成分方差的大小。
(3)将λ 排序:λ1≥λ2≥…≥λd,取前d′个特征值对应的特征向量构成投影矩阵W=(u1,u2,…,ud′)。其中,d′为降维后的维数,由各成分的累积贡献率决定,即:

一般Crate≥85%即可。
(4)根据W 求出低维空间的新特征量F=X*W 。
经PCA处理后的新特征最大程度代表了有用信息,剔除对应于d-d′个特征值的那些特征向量,使样本采样密度增大,一定程度起到去噪作用[16],作为下一步分类器的输入更佳。
3 数据处理及结果
3.1 预处理
为了使数据尽可能去除其他因素的影响,具有代表性,首先对原始EEG信号预处理。Cz电极一般作为参考电极,故本研究只选取C3和C4通道,图3为某次样本C3和C4通道原始信号。研究表明,人们在实施或仅是想象单侧手运动时,其对侧运动感觉区的μ节律(8~13 Hz)和β节律(18~30 Hz)会出现幅值降低的现象,称为事件相关去同步(Event-Related Desynchronization,ERD);其同侧运动感觉区的μ节律和β节律出现幅值升高的现象,称为事件相关同步(Event-Related Synchronization,ERS)[17]。因此滤除噪声及非相关的大脑活动频段,使信号更好体现运动想象特征。本研究选择FIR等波纹滤波器对包含140次信号的样本进行8~30 Hz带通滤波,滤波器参数设置为:通带截止频率分别为8和30 Hz,阻带截止频率分别为6和32 Hz,通带衰减为1 dB,阻带衰减为50 dB,密度因子为20。图4为滤波后的C3和C4通道信号,滤波后的EEG较好地消除噪声信号及无关思维信号的影响。
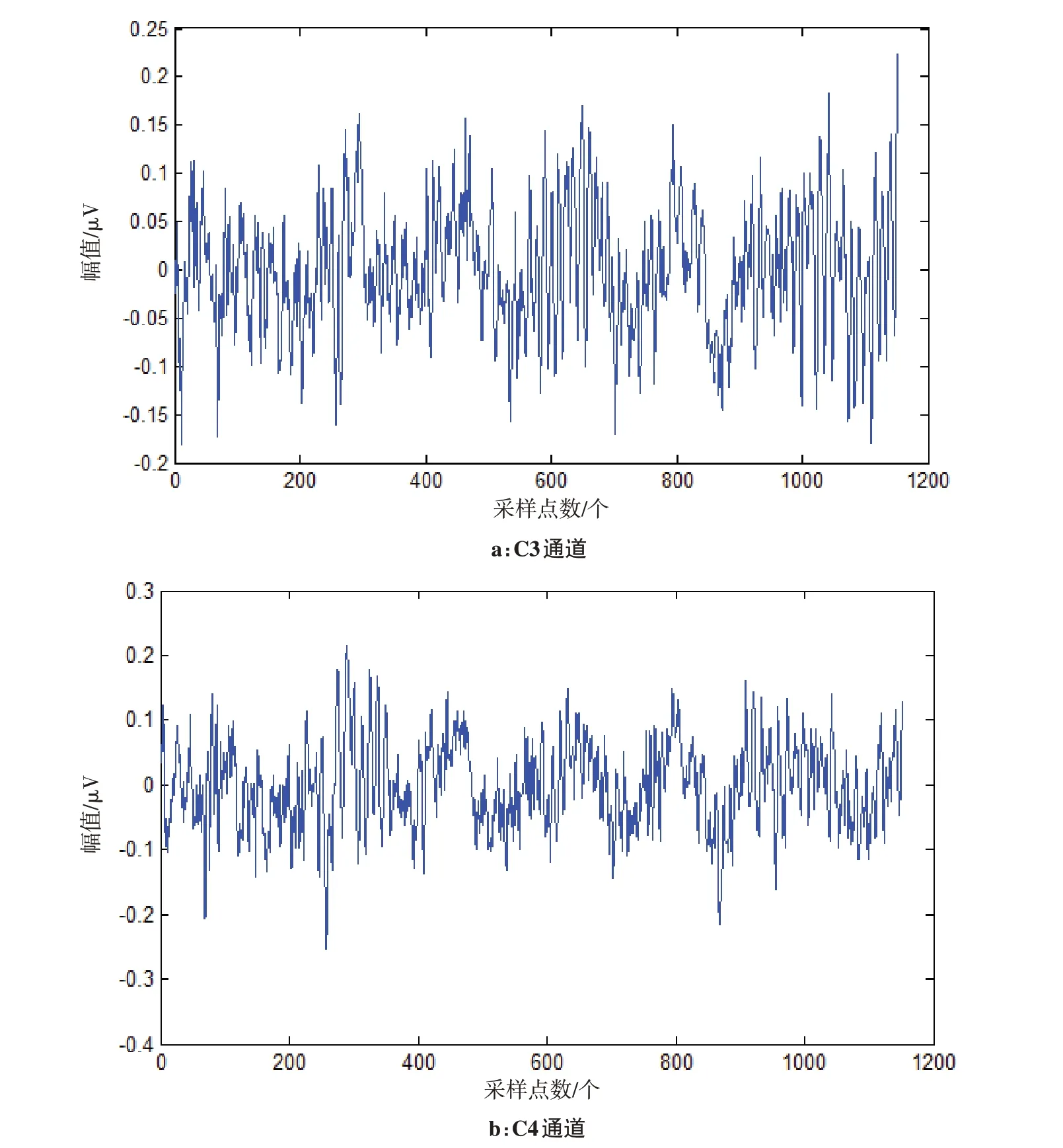
图3 原始EEG信号Fig.3 Original electroencephalogram(EEG)signals
由于数据采集过程中,第3秒才给予运动想象提示,且受试者有一定反应时间。且在图4中,该组信号对应类别号为1,即左手运动想象,可看出在第500个采样点后,与左手同侧的C3通道幅值增大,对侧的C4 通道幅值则较小,体现了一定的ERS/ERD 现象。因此本研究经过对比后,选取9 s数据中的4~8 s作为使用。数据采样率为128 Hz,单次实验时长9 s,则每次实验中每通道有1 152 个点,故应截取其中的第512~1 023 个点。此时数据为512×2×140,其中,512为采样点数,2为通道数,140为实验次数。
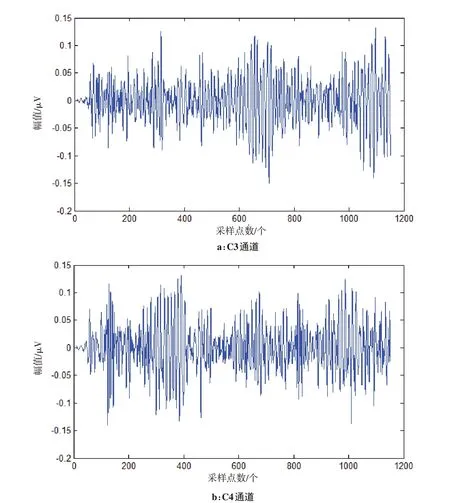
图4 滤波后的EEG信号Fig.4 Filtered EEG signals
3.2 特征提取与融合
(1)采用EMD 对预处理后的EEG 信号分解,得到一系列IMF。由于EMD 是一种自适应分解方法,因此无须提前确定分解阶数。图5和图6分别是C3和C4通道信号的IMF波形。
如图5和图6所示,信号被自适应地分解为imf1~imf6 共6 阶IMF 和残差(res),残差表示最终的信号趋势情况。从图中可以看出,C3和C4的趋势相反。在6阶IMF中,随着信号分解,频率不断降低,有用信息逐渐减少,因此仅选取能量最为集中的前三阶IMF进行特征值提取。由于ERS/ERD现象,C3和C4 通道的能量有所差别,故使用能量值作为特征。能量的计算公式为[18]:
其中,Ej,k为第j 个通道第k 个IMF 分量的能量,c(i)是IMF的第i个值,n为长度。每次样本可得到6维能量特征向量:
(2)使用CSP 提取空域特征值,它实质上是构造一组空间滤波器。对于二分类,可得到一对空间滤波器,则特征值为2 维,即每次样本得到的特征向量为:F2={f1,f2} 。
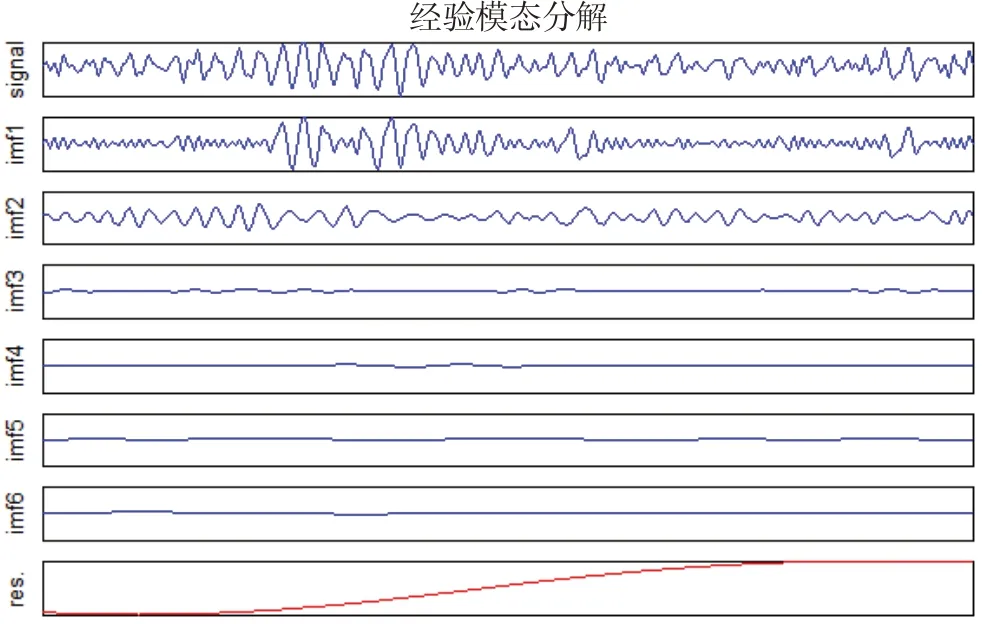
图5 C3通道的各阶IMFFig.5 Each order intrinsic mode functions(IMF)of channel C3
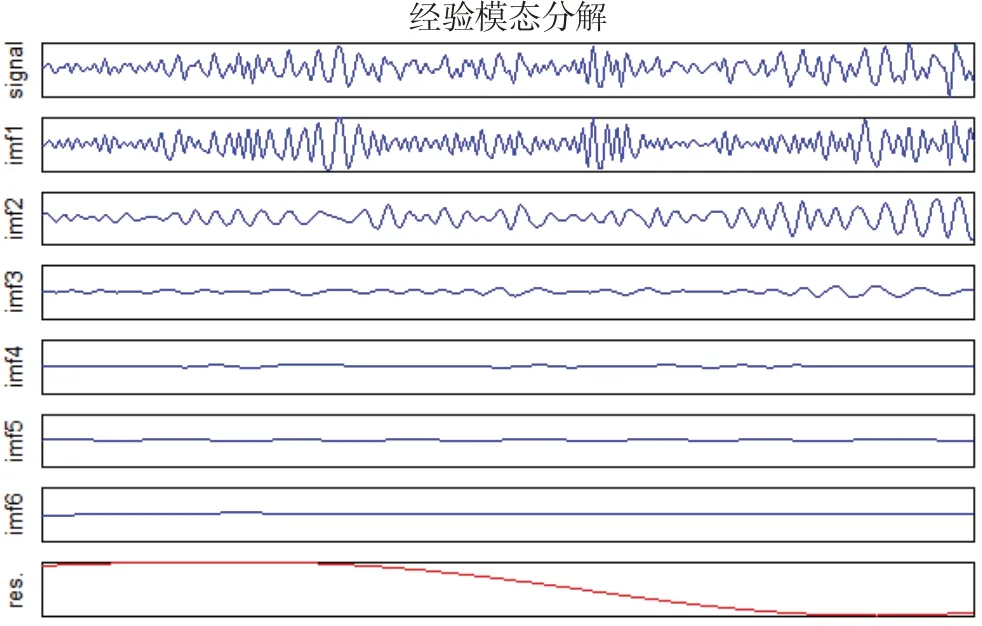
图6 C4通道的各阶IMFFig.6 Each order IMF of channel C4
(3)用AR 系数作为时域特征,本研究基于Burg算法进行模型系数估计,经过对比后确定阶数为6,则可相应得到6 个系数。对每次样本的C3 和C4 通道分别提取6个AR系数后,共可得到12维特征向量F3={a1,a2,a3,…,a12} ,其中,a1~a6为C3 通道的AR系数,a7~a12为C4通道的AR系数。
经过3种算法对EEG进行特征提取后,将每种特征向量进行合并,共可得到20 维时-频-空特征向量由于高维特征向量不利于分类器识别,且每种特征的重要程度不同,即对运动想象EEG分类的贡献率不同,用PCA降维以保留累积贡献率大于85%的主成分特征,得到6维的主成分特征向量F'。此时的特征向量F'最大程度体现了脑电特征,不仅减少了分类器的输入量,同时去除了贡献程度小的冗余信息,更加利于识别。
3.3 基于SVM的分类识别
基于统计学习理论的SVM是一种监督学习方法,对非线性、小样本及高维数据可取得理想的分类效果[19],基本思想是找到一个最优分类超平面,使它尽可能将两类样本点分开,且使间隔最大化[20]。本研究的SVM分类模型为C-SVC,经过对比后,选择RBF核函数。此外要确定SVM中的两个参数,惩罚因子C和核参数γ。本研究采用网格搜索法进行参数寻优,找到最佳的C和γ组合,分别以C和γ的取值范围作为网格边长,用合适的步进值交叉成一系列网格,则每个交叉点就是一组C和γ值,通过对这些点进行搜索,计算每一处的分类准确率,以找到使准确率最高时的C和γ值。在[0,1]内对特征向量归一化处理,首先粗略优化,在较大范围的搜索后将范围设置小一些,再精细优化,设置惩罚因子Cmin=-4,Cmax=4,核参数gmin=-4,gmax=4,步进值Cstep和gstep均为0.5。得到如图7所示的参数选择结果等高线图,可看出在不同的C和g组合时的准确率。得到Cbest=1.414 2,gbest=0.707 1,由于程序在实现时搜索的值为2的指数,即log2c 和log2g,即实际C的最优值为21.4142,γ 的最优值为20.7071,此时的最大分类准确率为91.9%。

图7 SVM参数选择结果图(等高线图)Fig.7 Support vector machine(SVM)parameter selection result(contour map)
3.4 结果对比分析
为验证本研究算法的有效性,做了两组对比实验。第一组是与单一特征及两两特征结合时的识别率对比,均使用SVM 识别,得到如表1所示的结果。如表1所示,使用单一特征值时,CSP的识别率最高,EMD的识别率最低;在特征两两结合时,识别率均大于80%,较单一特征有所提高,其中,CSP和AR模型结合时的识别率最高,同时由于单一特征时CSP 效果最好,在两两结合时,与CSP结合的两种算法较另一种都更高;而本研究采用的多特征融合方法,达到91.9%的准确率,明显高于其他6种,证明本研究特征提取算法的有效性。
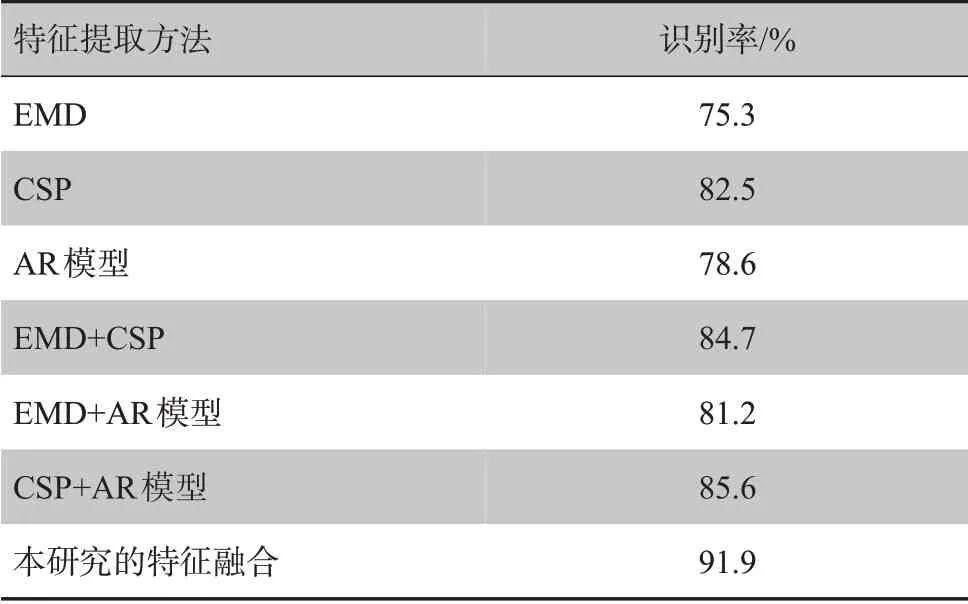
表1 不同特征下的SVM识别率对比Tab.1 Comparison of SVM recognition rate based on different features
第二组对比是将本研究的特征用另外两种分类器识别。选择BP神经网络和概率神经网络概率神经网络进行对比,均使用本研究特征作为输入,BP神经网络、概率神经网络和SVM 识别率分别为85.4%、83.6%、91.9%,BP神经网络和PNN的识别率均低于本研究通过参数寻优后的SVM,证明本研究SVM分类的有效性和可行性,说明将其与本研究的融合特征结合是相对匹配的。
4 结论
本研究对BCI2003 数据预处理后分别使用EMD、CSP、AR 模型3 种算法,得到时-频-空特征向量,用PCA 降维后,用SVM 分类,得到91.9%的识别率。同时做了两组对比实验,证明本研究多特征融合及SVM分类的有效性。运动想象脑电信号的识别作为BCI的关键环节,对BCI的功能准确度起到重要作用,而特征值的表征能力与脑电识别率密切相关。本研究的特征提取方法较以往单一特征得到较好的效果,可用于BCI对高识别率的要求。此外该算法可继续研究运动想象多分类,增加算法普适性。

