差分自回归移动平均模型与Elman神经网络及其组合模型对北京市肺结核发病预测效果的比较

闫银锁 孙闪华 李亚敏 李艳圆 赵鑫 陶荔莹 高志东

全国第五次结核病流行病学抽样调查结果显示，我国肺结核疫情呈现下降趋势，但不同地区有所差异[1]。“十二五”期间，我国肺结核报告发病率年递降率为3.0%[2]。北京市监测数据也显示，2005—2014年间肺结核发病状况整体呈下降趋势[3]。在北京市政府高度重视公共卫生和人民健康的背景下，做好肺结核发病情况预测评估，早期识别疫情变化及合理配置卫生资源是一个迫切而重要的问题。

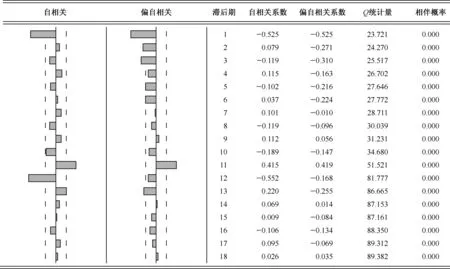
注 上图左侧垂直虚线为显著水平为α=0.05时的置信带图1 原始序列经一阶差分和季节差分后自相关及偏自相关系数图

时间序列分析是有效预测变化趋势的手段，已在公共卫生领域得到有效尝试[4-6]。由于不同传染病的传播途径不同，受自然环境和社会因素影响，不同地区的流行特征也不尽相同，因此选取恰当的模型是准确预测发病情况的关键。本研究比较可应用于传染病领域[7-8]的差分自回归移动平均(autoregressive integrated moving average，ARIMA)模型、Elman神经网络及ARIMA-Elman组合模型时间序列分析方法，评价其对北京市肺结核发病趋势的预测效果，寻找适合于北京地区肺结核流行特点的理想预测模型。

资料和方法

一、资料收集

肺结核发病数据来自《中国疾病预防控制信息系统》的子系统《结核病信息管理系统》，选择2010—2018年间现住址为北京市的肺结核发病数据作为研究对象，以Excel 2016软件统计月报告发病例数。其中2017年及以前各月份报告发病例数作为模型基础数据，2018年月报告发病例数作为模型验证数据。

二、研究方法

(一)模型建立

1．ARIMA模型建立：ARIMA模型作为自回归移动平均(autoregressive moving average，ARMA)模型的变体，是一类常用的随机时序模型，由Box和Jenkins创立，亦称B-J方法。它是一种精度较高的时序短期预测方法[9]。ARIMA模型用符号表示为ARIMA(p,d,q)(P,D,Q)s，参数p为非季节自回归阶数，d为一般差分阶数，q为非季节性滑动平均阶数；P为季节性自回归阶数，D为季节差分阶数，Q为季节性移动平均阶数，s为季节模型的时间单位周期[10]。在对一个时间序列建模时，应确定适宜的参数d、D、p、P，以及q和Q。

采用Eviews 9.0软件建立ARIMA模型，导入基础数据后进行模型识别。基础数据进行一阶差分后自相关系数(autocorrelation function，ACF)及偏自相关系数(partial autocorrelation function，PACF)图显示自相关及偏自相关系数快速落入随机区间，但滞后期(k)=12时样本的自相关系数显著不为零，表明季节特征存在。经季节差分后(图1)季节性特征有所减弱但仍然存在，经再次季节差分无明显改善，故此模型只选用一次季节差分。

对序列进行零均值检验，得到该序列样本平均数是-0.001，均值标准误为0.015，序列与0差异无统计学意义，可以直接建立ARIMA(p,d,q)(P,D,Q)s模型，根据差分后的ACF和PACF图截尾特征及模型检验结果(表1)，ARIMA(1, 1, 1)(1, 1, 1)12模型残差序列白噪声检验相伴概率为0.730，可认为残差序列满足随机性假设，其赤池信息量及贝叶斯信息量最小，选定为预测模型。

表1 ARIMA模型各待选参数检验结果

2．Elman神经网络建立：Elman神经网络是一种广泛使用的反馈型神经网络。因其具有较强的适应时变特性的能力，适合用于时间序列数据的预测研究[11]。Elman神经网络作为一种典型的非线性局部递归网络，在反馈型神经网络的基础上增加了一个承接层，承接层通过延迟储存反馈输入状态，以达到记忆的目的，使其对历史数据具有较强的敏感性，具有较强的动态学习能力。Elman神经网络由输入层、隐含层、承接层与输出层四部分组成(图2)。各层神经元节点数的确定对模型拟合优劣至关重要，也是建模的前提。

采用MATLAB R2014a软件建立Elman神经网络。神经网络模型要求训练数区间为[0, 1]的数据，因此建模前首先要将数据使用MATLAB软件中的mapminmax函数做归一化处理，输出结果之后再进行反归一化得到实际预测值。肺结核报告发病信息一般以月份进行统计，本研究即选取12作为输入层节点、1为承接层和输出层节点，隐含层节点数的确定尚未有一个很好的理论解析式，往往需要根据设计者的经验和多次实验来确定，本次建模以试凑法对4～21个不同隐含层节点数比较来确定。模型建立以误差0.0001作为训练目标，以1000作为训练步数，当隐含层节点数为10时(表2)，均方根误差(root mean squared error，RMSE)值最小，故Elman网络结构采用“输入层-隐含层-承接层-输出层”为“12-10-1-1”的形式。

图2 Elman神经网络结构[11]

3．ARIMA-Elman组合模型建立：对于肺结核发病数的预测，虽然多种模型可以实现，但各模型在不同实际情况下都存在一些自身缺陷，由此衍生出针对单一模型做局部调整和优化的方法。本研究采用误差倒数加权法将2种模型进行组合，首先计算单一模型均方根误差，使用其倒数作为各自权重值，最后将两部分迭加得到修正后的预测值(图3)。

图3 ARIMA-Elman组合模型建立方法

表2 不同隐含层节点数对Elman神经网络拟合度的影响

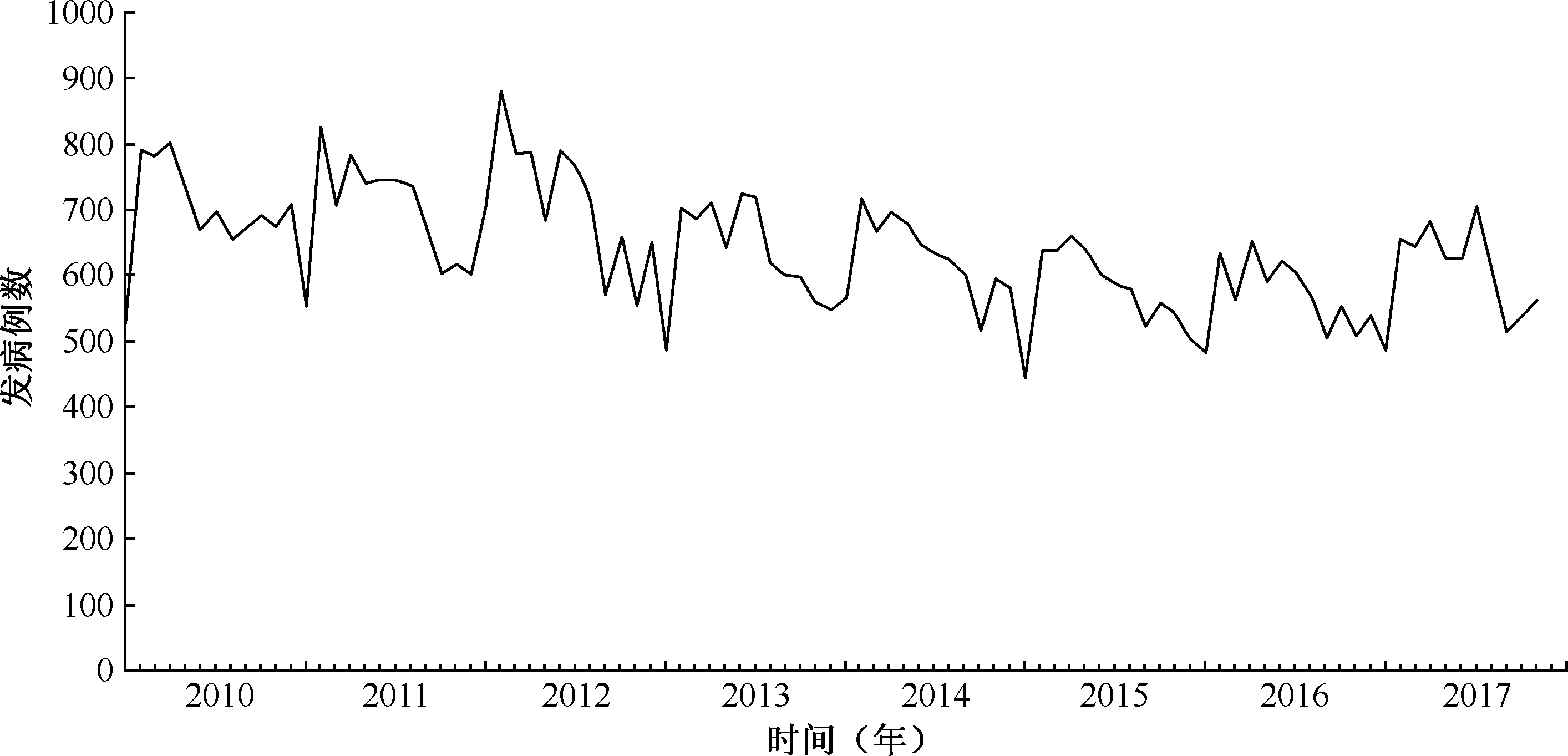
注 横坐标中短刻度线的单位为“月”，长刻度线的单位为“年”图4 2010—2017年北京市肺结核月报告发病例数趋势图

(二)预测效果评价

MAE是所有单个预测值与真实值误差的绝对值的平均，由于离差被绝对值化，不会出现正负相抵消的情况，是常用的基础的评估方法。MAPE不仅仅考虑预测值与真实值的误差，而且消除了时间序列数据水平和计量单位的影响。MAE指标为绝对度量值，MAPE指标为相对度量值。这些指标的值越小，说明模拟拟合效果越好。

三、统计学处理

采用SAS 9.2软件进行统计分析，对计数资料趋势分析使用Cochran-Armitage趋势检验，以P<0.05为差异有统计学意义。

结 果

一、肺结核发病形势

表3 2010—2017年北京市肺结核年报告

注较上年度变化率(%)=(当年发病例数-上一年发病例数)/上一年发病例数×100%

2010—2017年北京市肺结核报告发病例数月均641(7688/12)例，将肺结核月报告发病例数绘制成折线图(图4)，整体显示每年2月为报告发病的低谷，3月报告发病例数明显提升，后续各月报告发病例数波动中有所下降，月报告发病例数呈现一定规律的周期往复特点。

二、模型预测结果

以北京市2010—2017年间肺结核月发病例数作为基础数据，通过3种模型预测2018年北京市肺结核月发病例数，与当年实际报告发病例数进行对比，具体情况见表4。

表4 2018年1—12月模型预测发病例数与真实报告发病例数对比

注 左上、右上、左下图分别为ARIMA模型、Elman神经网络、ARIMA-Elman组合模型预测值与真实值对比图，右下图为3种模型与真实值的总体对比图5 2018年月报告发病例数预测值与真实值的对比分析

从预测值和实际值对比来看，ARIMA模型、Elman神经网络和ARIMA-Elman组合模型对北京市肺结核月发病数的预测相对误差多在±10%以内(分别为8个、8个和9个)。ARIMA模型预测结果相对误差在±10%～±20%的有3个，超过±20%的有1个；Elman神经网络预测结果相对误差在±10%～±20%的有2个，超过±20%的有2个；ARIMA-Elman组合模型预测结果相对误差在±10%～±20%的有3个，相对误差最大为19.1%。预测结果显示，将肺结核发病例数作为时间序列数据，并应用上述分析方法是可行的，但各模型预测结果的准确度有所不同。

可以观察到上述两种单一模型及组合模型预测结果是可以反映未来趋势的，但预测特征表现出差异(图5)。ARIMA模型预测结果整体较好，但在发病高峰及低谷月份预测结果与真实值对比波动较为缓和；Elman神经网络可以预测出各月份发病例数的变化趋势，但与真实值相比变化幅度较大；ARIMA-Elman组合模型在整体趋势及细节方面把握更为出色，尤其是2018年中后期预测结果更为准确。

三、模型评价与比较

通过MAE和MAPE客观评价3种模型的预测表现。ARIMA模型、Elman神经网络及ARIMA-Elman组合模型评价指标MAE值分别为44.7(536/12)、47.8(574/12)和43.8(526/12)，MAPE值分别为8.7%(1.039/12×100%)、8.2%(0.99/12×100%)和7.9%(0.953/12×100%)。对比结果可以看出，无论是MAE还是MAPE，组合模型获得了强于单一模型的预测能力，其预测准确率最高，更能够接近真实的肺结核报告发病情况。

讨 论

ARIMA模型、Elman神经网络及ARIMA-Elman 组合模型对于北京市肺结核发病的疫情预测上，是可以反映月发病变化趋势的。本研究中ARIMA 模型预测的相对误差多在±10%以内，但有个别月份的预测相对误差达到±10%甚至超过±20%，这个误差范围与付志勇等[12]对长沙市天心区肺结核发病例数的预测非常相近，但杨召等[13]使用该预测模型在某省肺结核发病率预测的MAPE仅为4.77%，相对本研究取得了更加理想的效果。多项研究结果也显示，ARIMA模型作为国内肺结核发病较为常用的预测方法，其应用的地区或范围不同，预测效果往往是存在差异的[14-16]。Elman神经网络虽适用于对时间序列数据进行拟合预测，但对比ARIMA模型来讲使用相对较少，在肺结核领域的应用更为鲜见，而多用于交通流量、网络流量等公共卫生以外的研究[17-18]。本研究Elman神经网络预测结果的MAE指标比ARIMA模型要大，但MAPE指标较小，说明Elman神经网络个别预测值波动较大。由于MAE为绝对度量值，相比MAPE来说对异常值变化更为敏感，单个预测值误差较大可以对整体误差产生较为明显的影响。

本研究中ARIMA-Elman组合模型基于误差倒数法进行组合，误差倒数法作为一种直观且便于理解的权值分配方法，在实际应用中已得到使用[19-20]。近10年来北京地区肺结核发病趋势预测多使用单一模型[21-23]，本研究在此基础上验证了将ARIMA-Elman组合模型应用于该领域的可行性。从3种模型对北京市肺结核发病趋势的预测评价指标来看，ARIMA-Elman组合模型比使用上述单一模型预测精度高、误差小，更适用于现阶段北京地区肺结核发病数的预测。

既往研究显示，单一预测模型通常仅能抓取已有数据的部分特征，通过一定规则将单一模型进行组合，可收集更全面的信息，从而提高预测精度[24-25]。ARIMA模型描述线性规律的能力较强，数据中的非线性规律则以残差的形式体现，理想情况下残差序列的自相关系数均为零，但在实际中这一要求往往无法达到。Elman神经网络最大的优势在于极强的非线性映射能力，其算法是采用基于梯度下降法，容易陷入局部极小点，对神经网络的训练较难达到全局最优。上述两种单一模型在预测中有着各自的优势，同时又都存在一定的局限性。ARIMA-Elman组合模型获取的信息更加全面，削弱了ARIMA模型对于残差中信息的缺失以及Elman神经网络反馈式学习的局限，得到的预测值有更理想的预测效果。

本研究也存在一定局限性。本研究以肺结核报告发病例数作为研究基础，实际情况下报告发病例数往往会低于真实发病例数，虽然有多种方式可以估算肺结核实际发病情况，但需要花费较大成本或使用限制较多[26]，因此获取真实肺结核发病例数相当困难。本研究以报告发病例数代替实际发病例数，数据的波动可能受到报告质量的影响。建模过程中，组合模型预测的方式有多种，较为常用方法包括等权重法、最小方差法、误差倒数法、调和平均法、主成分分析法等[27-28]。本研究中组合模型仅使用线性组合方法中的误差倒数法，而未对其他组合方法的预测效果进行验证。但现实中组合预测模型组合方式纷杂多样，依据实际情况探讨适宜的组合方法将是另一个值得深入研究的课题。本阶段主要在于模型的挑选，后续将尝试应用预测模型在北京市肺结核发病的预测中进行实际运用，借助该手段早期识别疫情变化及指导卫生资源配置，最大限度地发挥预测模型在实际应用中的作用。