基于GPU的线频调变标算法并行实现∗

唐扶光 刘 娅 钟何平

（1.武汉轻工大学电气与电子工程学院 武汉 430023）（2.海军工程大学海军水声技术研究所 武汉 430033）

1 引言

随着合成孔径声纳（SAS）技术的不断发展，成像分辨率不断提高，测绘带宽度不断加大，它们共同作用导致了用于成像的原始数据量显著增加［1～3］，严重影响着合成孔径声纳系统的实时成像。传统的距离多普勒成像算法［4］需要进行大量的插值运算，效率低下，而线性调频变标（CS）算法［5～7］中只用了FFT运算和复数乘/加运算，极大提高了成像效率，并且许多学者已经对其并行化方法进行了研究［8］。目前解决SAS的实时成像问题在硬件选择上通常有两种方案:1）专用硬件方案，其特点是计算速度快，价格昂贵，开发周期长，软件拓展性差；2）通用计算方案，其特点是编程灵活，开发周期短，软件拓展性好。目前的合成孔径成像通用计算方案主要采用的是计算机集群［9～11］，并且在合成孔径成像算法的并行化方面取得了较好效果。但集群运算的缺点是计算设备体积庞大，价格昂贵，功耗大。近年来出现的图形处理器（GPU）具有强大的浮点计算能力，并且NVIDIA公司提供多种CUDA环境下的常用函数库，大大降低了编程难度，使得GPU成为了一种通用的高密度计算设备。目前GPU已广泛应用于各种科学计算中，并且都取得了很好的加速比，这为合成孔径声纳CS算法的实时成像提供了新的途径［12～14］。

本文提出了一种GPU环境下的多子阵合成孔径声纳实时CS成像算法。首先分析了多子阵合成孔径声纳的CS算法成像基本流程，然后对算法中的多子阵回波向单子阵回波转化，方位向和距离向FFT变换和点乘运算的实现过程进行了GPU环境下的并行化设计，实现了GPU环境下的并行CS成像算法。最后通过实际SAS回波的成像试验，验证了所提并行CS成像算法的性能。

2 多子阵合成孔径声纳CS成像算法

多子阵合成孔径声纳CS成像算法的基础是CS算法，该算法思想是基于线性调频信号尺度变换的特点，然后采用CS操作消除距离徙动随距离的空变特性，使得不同距离上的点目标距离徙动轨迹相同，再通过在二维频域上乘一个线性相位因子完成所有的距离徙动校正，从而避免插值操作［15～16］。CS算法优点是不需要耗时的插值运算，只需要快速傅立叶变换和复数相乘就能完成距离迁徙的校正，使得成像效率大大提高，而且便于并行运算，相位保真度高。存在不足的是，CS算法是基于线性调频信号发展起来的，因此它仅限于此种信号形式。基于CS算法的多子阵SAS成像算法的基本流程如图1所示，主要分为以下几个步骤:

1）根据等效相位中心近似条件PRI*V=D*M/2，确定有效子阵个数M，并进行阵元信号的重排。式中V表示声基阵载体速度，PRI表示脉冲重复间隔，D表示阵元尺寸。

2）对多子阵SAS由单发多收和非停走停模式引入的固定相位误差采用等效相位中心近似进行补偿。

3）在距离时域、方位频域采用CS算法原理将不同距离上的目标徙动轨迹校正到与参考距离上的目标徙动相同。

4）将距离向变为频域，在二维频域中同时完成距离压缩和距离徙动校正。

5）在距离时域、方位频域进行方位脉冲压缩和剩余相位补偿。

多子阵合成孔径声纳CS成像算法从计算角度看主要包含复数点乘、FFT和IFFT运算。但随着合成孔径声纳技术的发展，用于成像的原始数据维数越来越大，这三类基本运算的速度严重影响着CS算法的实时性。GPU中的大量并行计算单元为复数点乘、FFT和IFFT快速计算提供了基础。此外，NVIDIA公司提供的CUDA编程环境中包含高效的FFT和IFFT函数库，在加速FFT和IFFT计算的同时，极大简化了GPU应用程序开发。

图1 CS算法流程图

3 CS成像算法的并行化

3.1 多子阵SAS回波向单子阵SAS回波并行转化

多子阵SAS成像的最简单方式就是将多子阵回波数据先等效为单子阵回波数据，然后采用单子阵合成孔径成像算法进行处理。多子阵SAS回波向单子阵回波转化需要经过两个步骤:1）有效数据截取；2）固定相位补偿。由于实际SAS系统中子阵个数M与阵元长度D、平台速度V、脉冲重复间隔PRI不能恰好满足临界条件:PRI*V=D*M/2，一般作业过程中要求实际平台运动速度V0＜D*M/2/PRI，此时成像需要的有效阵元数M0=2V0*PRI/D。由于采集原始信号是先按阵元后按脉冲顺序排列的，因此对连续脉冲数据进行有效截取可以直接采用高效内存拷贝函数memcpy完成。固定相位补偿分块示意如图2所示，M0表示有效子阵数，Nr表示距离向点数，K表示当前处理数据块的脉冲个数。完成有效数据截取后，原始数据是以二维形式存储的，二维数据的行数为M0*K，列数为Nr。如果把原始信号抽象为三维Nr*M0*K形式，每一个脉冲内数据一层，然后按照脉冲顺序将回波层叠放置，因此固定相位补偿线程分块适合采用三维形式。假设单个三维线程块的维数为BI*BJ*BK，则总的三维线程分块数为TBI*TBJ*TBK，其中TBI=（Nr+BI-1）/BI，TBJ=（M0+BJ-1）/BJ，TBK=（K+BK-1）/BK。现假设当前线程块的索引为（Si，Sj，Sk），线程块内线程索引为（Ti，Tj，Tk），则当前线程处理的数据行坐标TNr=BI*Si+Ti，列坐标TNa=（BJ*Sj+Tj）+M0*（BK*Sk+Tk）。建立线程索引与原始回波数据的对应关系后，只需在时域中与相位补偿因子相乘即可，其中 f0为中心频率，c为声速，r为距离，v载体速度，Δhi为第i个接收阵中心与发射阵中心的距离。

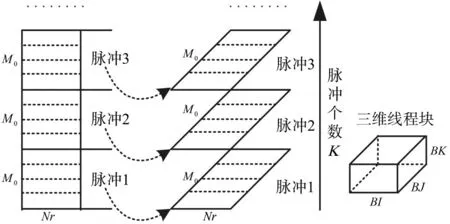
图2 固定相位补偿分块示意图

3.2 距离向和方位向FFT变换

高效FFT变换是合成孔径声纳CS算法快速成像的基础，CUDA中提供高效的FFT函数库极大简化了CS算法的实现过程。在CS算法实现过程中，距离向和方位向FFT变换都是一维变换，这一过程的实现是通过调用CUDA中cufftExecC2C（cufftHandle plan， cufftComplex*idata， cufftComplex*odata，int direction）函数实现的，其中plan用于指定FFT变换基本参数，包括数据类型、一次FFT变换点数和FFT连续变换次数，idata表示输出数据地址，odata表示输出结果地址，direction表示FFT正变换/反变换。对于距离向的FFT正/逆变换可以直接通过调用cufftExecC2C函数来完成，在构造FFT变换句柄plan时，指定一次FFT变换的点数为距离向点数Nr，连续变换次数为方位向点数Na。

方位向FFT变换不能直接调用cufftExecC2C函数，因为在内存中方位向数据不是连续存储的。为了满足cufftExecC2C函数FFT变换要求，必须先进行矩阵转置操作，将方位向数据变为内存中的连续存储形式。在采用CUDA进行矩阵转置时，线程块先采用合并方式读入对应的原始数据，在线程块内部完成局部数据块的转置操作，然后再采用合并方式将转置后的结果写入显存。采用合并访问方式可以有效避免数据访问冲突，提高数据访问速度。完成矩阵转置后，调用cufftExecC2C函数来进行方位向FFT正/逆变换，这时一次FFT变换的点数为方位向点数Na，连续变换次数为距离向点数Nr。最后再进行一次矩阵转置，完成方位向FFT变换。

3.3 CS算法中的点乘运算并行

将多子阵回波数据等效为单子阵回波以后，单阵CS算法在成像过程中共需三次进行点成运算:1）在距离时域-方位频域（tr-fa）将不同距离的徙动曲线校正成一样；2）在距离频域-方位频域（fr-fa）对不同距离的回波进行统一的距离徙动校正；3）在距离时域-方位频域（tr-fa）进行剩余相位补偿。在这三部分点乘运算中，1）和3）是在距离向上依次对每列数据进行点乘运算，2）是在方位向上依次对每行进行点乘运算，它们的共同点是对每行或每列进行点乘运算时不存在先后顺序。对于CS算法中点乘运算采用一维线程组完成，假设线程组的维数为L×1，原始回波数据距离向和方位向维数分别为Nr×Na，在进行计算任务分配时，行坐标为Tnr的列采用线程Tnr mod L计算点乘，列坐标为Tna的行采用线程Tna mod L计算点乘，这样可以最大限度地均衡使用计算资源。在进行点乘运算前，计算过程经常使用的常量，包括距离向距离和频率坐标、方位向距离和频率坐标、CS因子等先在主机中完成计算，再上传至显存，这样进行点乘计算时可以直接使用，避免重复计算，节省计算时间。

4 试验结果与分析

为了验证本文所提CS并行成像算法性能，在如下计算环境中进行了成像试验:处理器Intel（R）Xeon（R）CPU X5650 2.67G（2处理器12核）；内存48G；显卡Tesla C2050；操作系统Windows 7专业版；软件环境VS2008。为了充分验证所提算法性能，在上述环境下分别进行了单核CS算法成像、多核CS算法成像和GPU环境下的CS算法成像。

成像试验中选用的原始数据是在千岛湖进行干涉合成孔径声纳海试样机试验中获取的，对应的幅度信息如图3（a）所示，最近采样距离为51m，最远采样距离231m，其距离向和方位向点数分别为9600和2880。从图3（a）中可以看出远距离处信号回波较弱。试验系统基本参数如表1所示。

表1 试验系统基本参数

三种计算方式下的CS算法成像结果分别如图3（b）～（d）所示，可以看出三种成像结果是一致的，成像结果非常清晰，满足水下高分辨率成像需求，为水下小目标探测提供了保证。

图3 CS算法成像结果

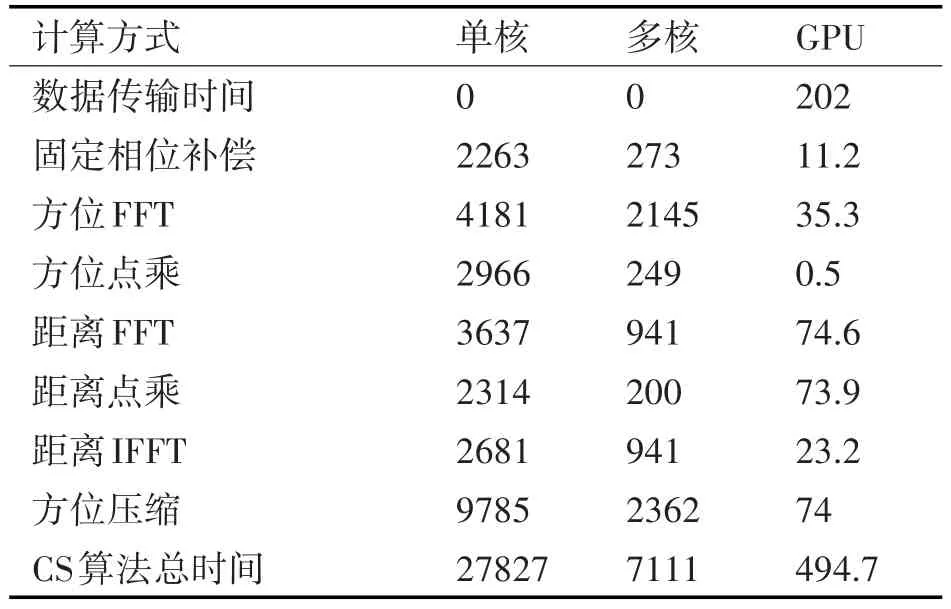
表2 CS算法成像效率比较（ms）

三种计算方式下的CS算法效率比较如表2所示。从表2中可以看出，采用单核和多核计算时，不需要进行数据传输。对于原始测试回波，采用CS单核成像算法，总的计算时间为27827ms。在共享内存环境下，采用OpenMP并行后，总的计算时间降为7111ms，加速比为3.91。采用GPU计算，虽然需要进行数据的上传和下载操作，但因数据传输带宽大，对于测试数据仅为202ms。由于采用了CUDA中高效的FFT变换函数库，成像部分的FFT运算时间大幅度减小，此外算法中的点乘运算效率也大幅度提高。最后基于GPU的并行算法成像时间降为494.7ms，与单核计算相比，加速比达到56.25，满足SAS实时成像需要。

5 结语

本文提出了一种基于GPU的实时合成孔径声纳CS成像算法。给出了多子阵合成孔径声纳CS成像算法的基本流程，单子阵SAS回波向单子阵回波转换、方位向和距离向FFT变换和点乘运算的GPU并行实现方法。最后在GPU并行平台上进行了CS算法成像试验，验证了所提并行算法性能，满足SAS成像的实时性需求。