基于扩展卡尔曼滤波的水下目标运动轨迹分析算法∗
刘兆才 刘 杰 徐学伟
(91388部队41分队 湛江 524022)
1 引言
对水下目标的探测一般使用声学方式进行探测,声纳探测器收集的水下目标信息能够反应目标运动性质,但目标回波往往参杂了噪声信号使探测数据有一定的随机误差[1]。一般方法不能很好地对噪声信号进行滤波处理,导致对目标运动的数据处理精度降低甚至发散。经典卡尔曼滤波对噪声特征变化的适应能力差,并且目标运动方程往往具有不同程度的非线性特性。因此考虑使用扩展卡尔曼滤波的算法将离散信号进行滤波处理,还原出目标运动轨迹[2]。本文探讨一种基于扩展卡尔曼滤波的水下目标数据处理方法,并与原始目标真实运动轨迹数据进行比较,验证此方法的有效性,为探测系统生成水下目标态势提供支撑。
2 扩展卡尔曼滤波算法
扩展卡尔曼算法(EKF)的基本思想是将非线性系统线性化,也就是将非线性函数进行泰勒展开并略去高阶项,然后进行卡尔曼滤波[4]。

图1 滤波流程示意图
2.1 非线性系统模型
在非线性系统中,状态向量与其系数是不能分离的。系统状态方程[3]如下:
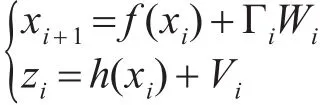
W与V分别代表过程噪声和测量噪声,数学期望均为0,方差分别为Q、R,x代表系统状态,且W与V非线性相关。
利用非线性函数的泰勒展开,将系统模型截断至二次项,忽略其余高阶项,相比一阶线性化截断可有效减少由于线性化引起的估计误差。
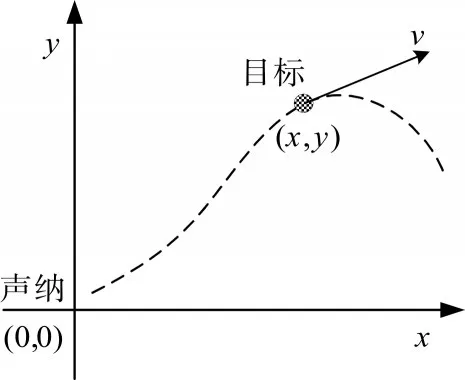
图2 目标运动示意图
2.2 线性化求解
由于目标运动轨迹是连续的,可以将非线性系统的动态特征变成线性的动态特征[6]。线性卡尔曼滤波中的状态转移矩阵A和观测矩阵H由f和h函数的雅可比矩阵代替,n维状态的求法如下:
线性化后,依据卡尔曼滤波的迭代方法[5]计算,计算过程如下式:

2.3 线性化后的滤波模型流程[9]
线性化后的滤波模型流程如图3所示。
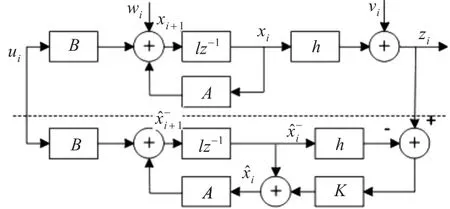
图3 滤波处理流程图
3 目标轨迹信息估计
平面运动物体的运动状态主要由位置、速度、加速度等决定,引入状态向量如下:X=[x,vx,ax,y,vy,ay]T,式中 x、vx、ax、y、vy、ay分别表示目标在X、Y坐标系中的位置、速度、加速度分量。系统t+T时刻状态方程为[7]
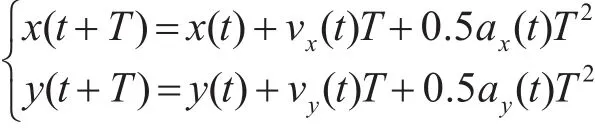
测量向量选取x、y坐标轴上的点,表示为Z=[x,y]T加入系统过程误差和测量误差,则系统方程表示为[8]
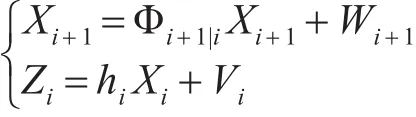
系统过程噪声W及测量噪声V均为不相关的白噪声,即其期望值为0。其中Φ、h如下式[10]:

令过程噪声方差矩阵为Qi=E(WiWTi),系统测量噪声方差矩阵为Ri=E(ViVTi),计算得到Q与R。根据卡尔曼滤波流程,在方差矩阵及Φi+1|i已知的情况下,可通过 Xˆ0、P0及i时刻观测值Zi,即可得到系统状态的最优估计[11]。
4 试验及分析
为对上述算法性能进行分析验证,使用Matlab工具模拟水下目标航迹,并通过加入随机观测误差Ri的方式来模拟实际的测量值zi。假设水下目标初始段航向30°,末段做120°的机动旋回。数据采样周期为20s,采样点数为80点,测量噪声误差 ≤0.5。
设置系统初始位置xˆ0及协方差矩阵P0为

滤波前真实目标轨迹与测量轨迹如图4。
对测量值zi滤波后的轨迹图如图5。
通过计算系统测量值zi与真实目标轨迹一次差及滤波后轨迹一次差,滤波前后的一次差如图6所示。滤波前轨迹测量值的二阶原点距约为0.41,滤波后轨迹的二阶原点距约为0.15(中段15点统计值)。与滤波后的轨迹滤波后的目标轨迹与实际轨迹的二阶原点距减小了约65%,表明此方法可有效降低因观测误差导致的水下目标轨迹跳变大的影响,同时可有效提高轨迹测量精度,为后续水下目标的运动要素解算提供支持。
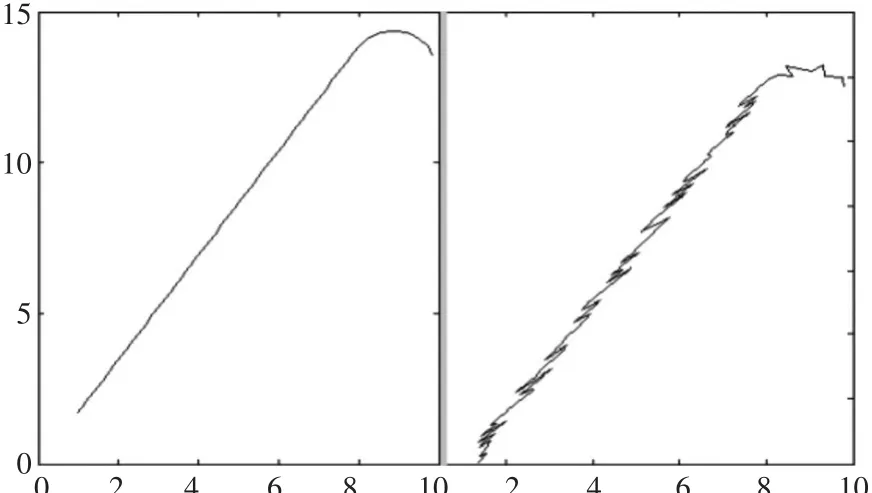
图4 真实—测量目标轨迹图
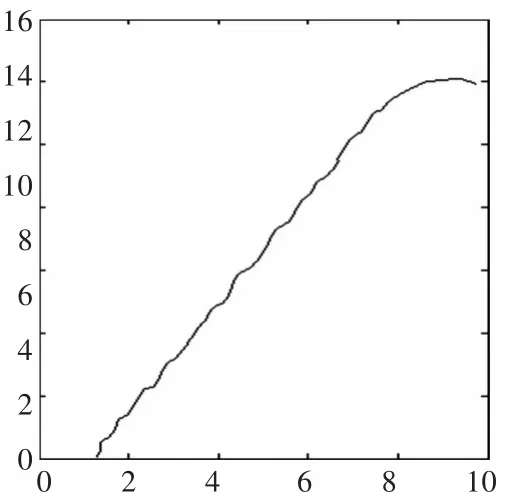
图5 滤波后目标轨迹图
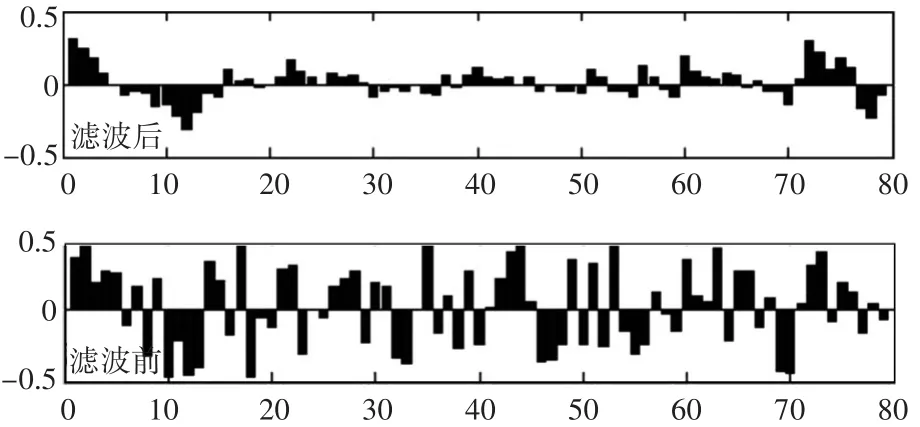
图6 滤波前后一次差
5 结语
本文针对水下目标轨迹测量存在的观测误差大且运动非线性的特点,利用扩展卡尔曼滤波器(EKF)完成了水下运动目标轨迹的滤波算法设计。同时通过实验分析,表明了在目标做简单机动时,扩展卡尔曼滤波(EKF)算法能够很好地对目标运动轨迹进行估计,可以较准确还原水下目标的运动轨迹,为进一步的目标运动要素等的数据处理提供支撑。但是这一方法并未考虑水下目标变深机动的情况,下一步将研究如何将此方法应用到水下目标三维运动轨迹的处理中。

