察打一体无人机末端突防路径规划方法研究∗
胡艺铭 孙春生 李佳宽 于洪志
(海军工程大学兵器工程学院 武汉 430033)
1 引言
无人机航迹规划为在特定目标和约束条件下,寻找从给定起点到设定终点、航迹代价最优的无人机飞行路径的行为。一般来说,需要考虑的约束条件有无人机系统的机动特性和威胁环境要素等。航迹规划在无人机的任务规划系统中占据着极其重要的地位,是无人机任务保障的核心技术[1]。
航迹规划问题实际上是多条件约束下的最优化问题,其中约束条件和优化求解分别涉及到数学物理建模和优化算法,因此航迹规划一直是任务规划系统中的重难点问题。在现有的航迹规划中,有环境要素和规划方法两方面因素需要考虑,其中环境因素,主要包括地形和敌方防空系统,地形通常利用高程数据建立,防空系统以考虑雷达影响为主,在现有的无人机路径规划文献中,一般采用传统的雷达探测空间模型[1~2],但该模型不能真实地体现出雷达的探测空间;对于规划方法,常用方法有网格规划法、概率图规划法、人工势场法、智能算法等[4~6],其中智能算法往往收敛较慢,人工势场法容易陷入局部最优解,经典的网格规划算法,如A*和D*算法[7],虽然它们往往能够计算出分辨率最优的路径,但是与概率图算法相比较,却受限于低维度空间,而概率图算法中的基于模拟退火的双向RRT算法[8]可以在三维的规划空间中得到概率最优的路径。论文以察打一体无人机末端突防航迹规划为背景,首先建立以飞行路径最短和被探测概率最小为目标的最优化模型,然后采用基于混合采样的雷达模型和基于模拟退火的双向RRT算法等改进手段对最优化模型进行了细化和求解,实现了无人机末端突防航迹的合理规划。
2 无人机航迹规划模型
2.1 最优化模型
将无人机的任务区域称为配置空间δ,该区域中地形和雷达将δ空间分为三个空间,其中地形占据区域为障碍空间δoi,即无人机无法飞行的区域;雷达空间为半自由空间δfree*,在该空间中需要考虑代价函数c:δfree*→,即在每一个配置点q∈δfree*都对应一个代价代表着雷达的探测概率值以及自由空间δfree。
有了上述的空间定义之后,论文不妨定义无人机飞行路径ρ的长度为l,为建立以飞行路径最短和被探测概率最小为目标的最优化模型,将路径分为 Nbt段,(xu,yu,zu)为路径上每段的终点坐标,(xrd,yrd,zrd)为配置空间中雷达所在点的坐标,(xwo,ywo,zwo)为地形高程数据的坐标值,w1,w2分别为每段路径长度和探测概率的权值,L为航路的总长度,TNi为路径上的探测概率,Rru,m代表雷达与目标的距离。接下来就可以得到无人机航迹规划的最优化模型:
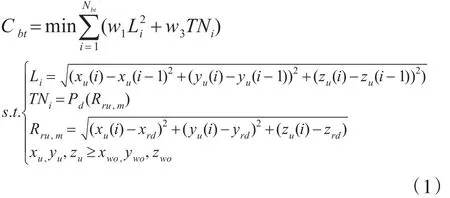
式(1)中(xwo,ywo,zwo)涉及数字高程地形模型的选取,TNi受雷达探测模型和地形模型共同影响,下面将分别介绍。
2.2 数字高程地形模型
在最优化模型公式中,有 xu,yu,zu≥xwo,ywo,zwo,即要求无人机飞行时始终避开障碍空间;因此,为了得到无人机飞行中障碍空间,需要采用了数字高程模型建立地形
目前,对于无人机对地打击的地形建模的数据来源,一般来自于美国太空总署(NASA)和美国国防部国家测绘局(NIMA)联合测量的SRTM(Shuttle Radar Topography Mission)数据库。该数据库包含世界大约80%的数字高程模型,且分辨率高达 90m[9]。
这里选取了经度从100.402°到100.774°及北纬从28.395°到28.024°的高程数据,地形如图1所示。
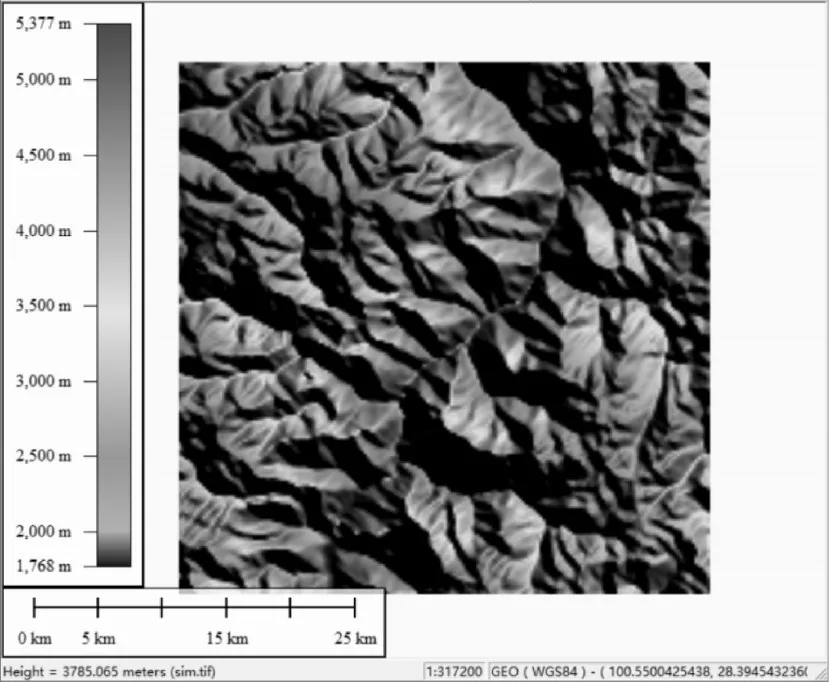
图1 数字高程模型地形
上述高程数据,在Python的GDAL环境中三维表示如图2所示。
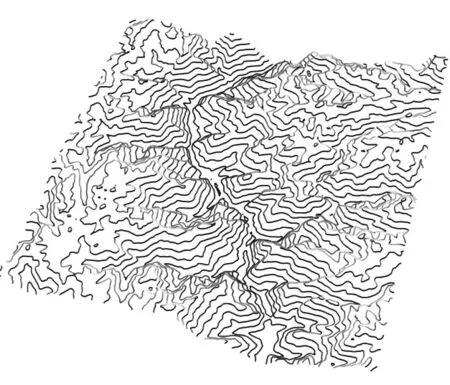
图2 地形三维图
2.3 探测雷达模型
为了更加真实地表现出最优化模型中雷达的探测区域,即半自由空间TNi所包含的空间范围,来用于无人机的末端突防,论文采用基于混合采样的雷达作用范围三维建模方法[9]。
本论文考虑的雷达自由空间中的单基地雷达,所以雷达的发射能量和接受能量都由同一根天线决定,所以探测区域可以表示为
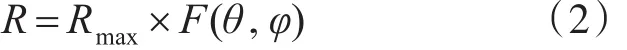
式中,Rmax为雷达最大探测距离,F(θ,φ)中θ为方位角,φ为俯仰角。在自由空间中的,不考虑各类影响电磁波传播环境因素的,方向图传播因子F(θ,φ)只与雷达天线方向图函数有关的雷达。故在上述约定条件下,公式的 Rmax和 F(θ,φ)分别表示如下:
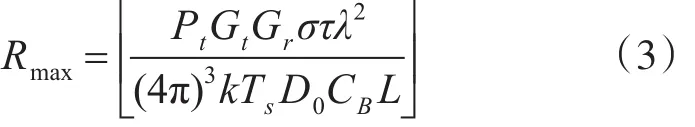
其中Pt为天线发射功率,Gt为发射天线增益,Gr为接受天线增益,σ为雷达目标截面积,λ为雷达波波长,k为玻尔兹曼常数,Ts为接收系统噪声温度,D0为检测因子,CB为带宽校正系数,L为系统损耗因子。
式(2)中F函数,论文采用高斯型方向函数[11],即式(4),其中θb为波束宽度。
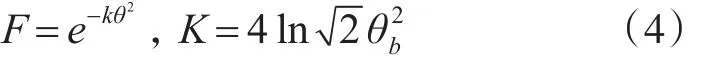
有了上述的探测雷达模型后,通过Python的mayavi环境,可以直观看到雷达探测范围如图3所示。

图3 雷达探测范围三维显示
2.4 地形遮蔽条件下雷达探测范围的修正
雷达的探测范围 TNi还会受到地形的影响,论文采用几何光学的方法对遮蔽问题进行处理。一般来说,地形的遮蔽情况为多峰,下面详细说明多峰遮蔽情形。
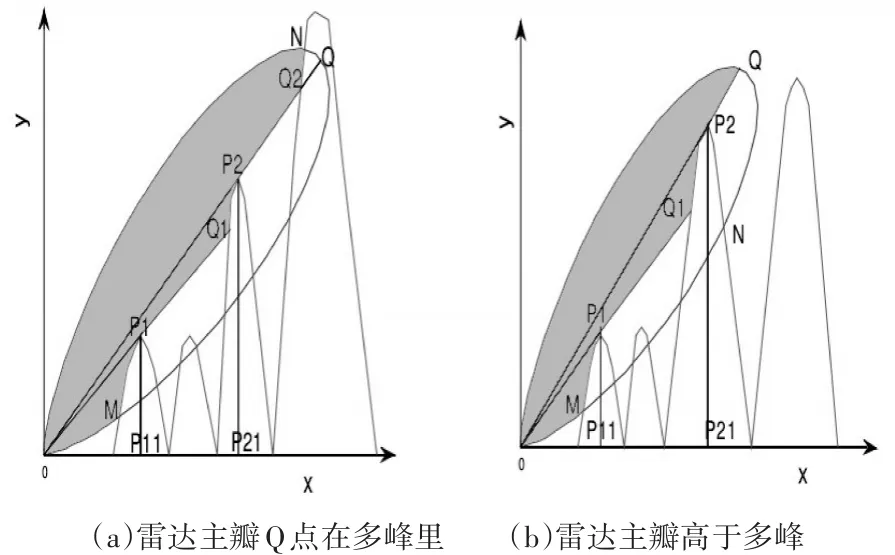
图4 多峰地形对雷达探测边界示意图
连续多峰对雷达的影响分为两类,一类情况多峰的末交点高于雷达主瓣的Q点,如图4(a),另一类情况多峰的末交点低于雷达主瓣的Q点,如图4(b)所示,在这两种情况下,雷达的探测区域都被修正为灰色区域,对应半自由空间,其中雷达主瓣被遮蔽部分为自由空间,多峰所在区域为障碍空间,即雷达探测空间被修正为半自由空间、自由空间和障碍空间三部分。
2.5 雷达探测概率原理
明确了地形遮蔽条件的雷达探测空间之后,还需要对其中半自由空间中的雷达探测概率TNi进行定量描述,以进一步用于无人机突防威胁代价的计算。
总的来说,雷达探测概率(Pd)与雷达信号的信噪比(SNR)有关,而信号的信噪比(SNR)又与探测目标与雷达的距离(Range)有关。详细来说,在文献[14]中,雷达探测概率 Pd可以重写为Marcum Q函数,即式(5)。
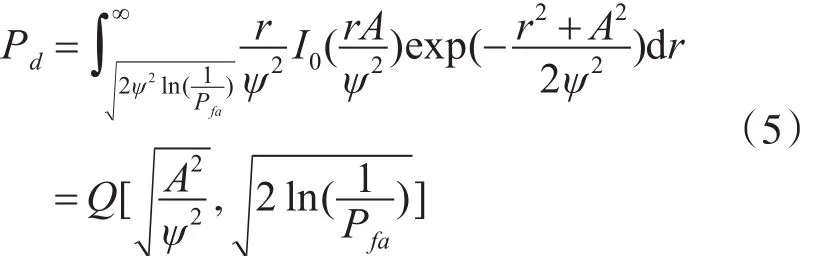
式中,A为雷达信号的幅度,ψ2为雷达噪声的方差,pfa为雷达的虚警概率。由于过式(5)即可以算出Pd与SNR的关系。
为了进一步考虑目标距离与雷达探测概率的关系,需要分析雷达信号的信噪比的具体表达式[14]:
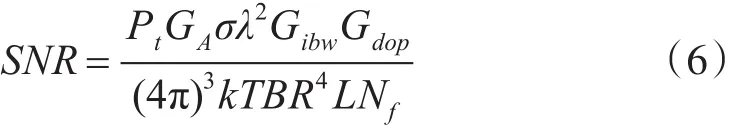
其中Pt为峰值发射功率,GA为天线增益,σ为雷达目标截面积,λ为发射载波波长,Gibw为时域带宽增益,Gdop为多普勒处理增益,K为玻尔兹曼常数,T为环境温度,B为传输信号调制带宽,R为目标距离,L为系统损失,Nf为噪声系数。
通过2.3和2.4节,确定了雷达的探测区域,而通过2.5节,论文确定了雷达探测区域中雷达的探测概率。
3 航迹规划算法
对于在给定起终点的情况下,在雷达威胁区域中寻找到一条路径最短探测概率最小的路径,即求解式(1),论文采用基于模拟退火的改进双边RRT(Rapidly-exploring random)算法;这里首先介绍该算法的评价准则,该准则引导路径在低探测度区域搜索;然后介绍该算法如何实现。
对于算法的评价准则来说,一个关键点是,从力学角度来看,路径上的点探测概率的增加(或者叫做路径代价的增加)会对路径的选取产生斥力;所以,评价一条路径的好坏是以路径上点的探测概率高低为标准的,同时,在路径的距离上加上一个小的惩罚变量,用于在同样的斥力情况下,选择路径较短的那一条。基于这种原则,路径上的斥力定义为

其中 p+代表路径中探测概率增加的部分,ε相比于路径的代价值非常小,L表示飞机路径。
w的连续形式能够转化为便于求解的离散形式,考虑到路径上的局部极值,w表达式为
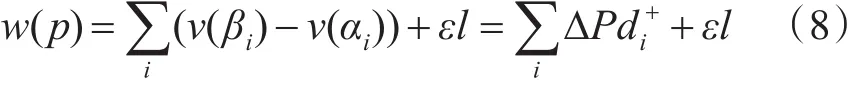
其中αi和 βi是路径上的局部的最小和最大值,=Pd(βi)-Pd(αi)两个极值之间的正变化;如图4,总之,路径的斥力(或代价值)是通过计算极值之间的正变化,并且在路径中加入一个εl参数以用来选择斥力相同,路径较短的那一条。
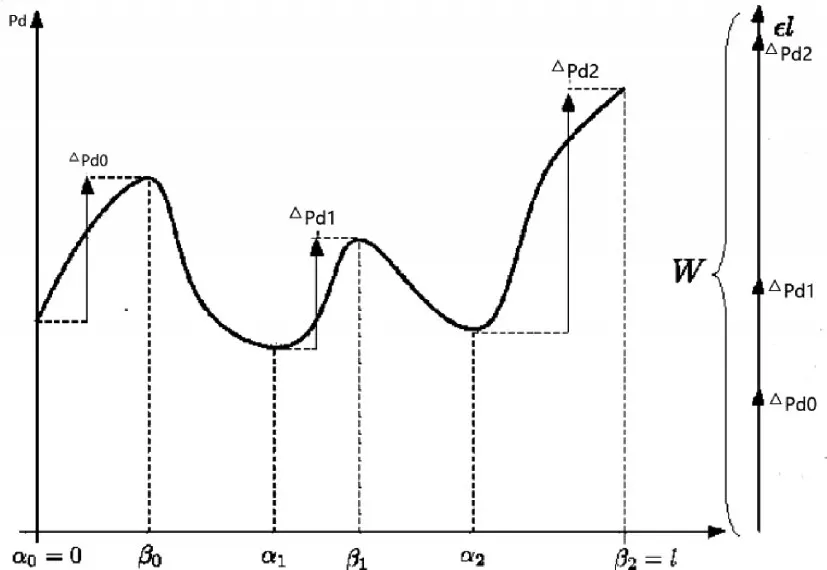
图5 路径代价值为Pd增加段之和
值得注意的是,上述描述中,只考虑了路径中探测概率增大的路径段,对于探测概率减小的路径段,算法控制该阶段的路径长度,以控制总路径的长度,具体的证明如下。
一般来说,路径总代价值为探测概率增大和探测概率减小段之和,公式表示如下:
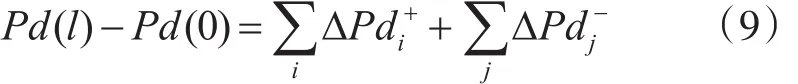
通过式(7)、式(8)可以转化成
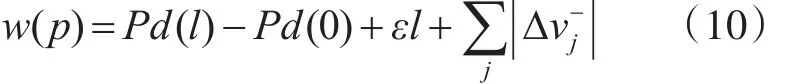
因为 Pd(l)和Pd(0)为常数,而εl相对于代价值非常小,故式(10)说明最小化w相当于最小化最右端那一项。
论文采用的算法来同时具备快速扩展随机算法的探索能力和随机优化方法在复杂空间中求解全局最小值的能力。换句话说,它使用转移测试来接受和拒绝潜在探测概率较小或较大的状态。转移测试算法具体实现如下。
首先,在雷达探测空间中,高于最大探测概率的Cmax将被舍弃掉,接下来,采用与Monte Carlo方法类似的思路,新配置点被接受的概率是通过比较其探测概率与其父节点的探测概率的差值来得到的。转移概率 pij被定义如下:
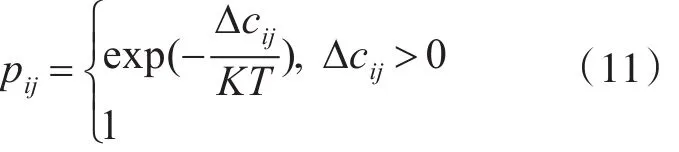
其中Δcij=(Pdj-Pdi)/dij是代价函数的斜率,即探测概率差值除以两者之间的距离。K是常数,用于正则化表达式;T是温度参数,用于控制转化测试的难易程度。
使用该转移概率参数,探测概率的下降的位置点将会被自动接受,而探测概率的上升,随着探测概率差值的增加,被接受的概率将指数下降。
在上述的算法中,有一点是论文想要强调的,温度参数T,它是算法的核心参数,它决定了探测概率差值被接受的难易程度,低温度情况下,限制了对小差值的扩展,反过来,高温度下,允许大差值的扩展。同Monte Carlo方法类似,该参数在探索过程中,是保持不变或者逐渐较小的。
介绍了算法中核心的自适应参数后,最后介绍算法的概率完备性,由于论文算法是基于RRT算法,它继承了RRT算法的概率完备性[8];唯一一点不同是,由于转移测试的因素,一些扩展点会被舍弃掉,即使在高维凸空间中。

图6 无人机的起始终止位置
为了验证本文的算法,将不考虑机动约束,匀速飞行的无人设定从(9.752km,14.304km,3.8km)的起始位置飞往目标位置(8.05km,12km,2.0km),公式中的参数皆取经验值。计算结果,如图6所示。
图6中雷达的位置中心设定为(7.5km,12km),最终通过本文的算法可以得到如下的路径,和路径上的探测概率值。
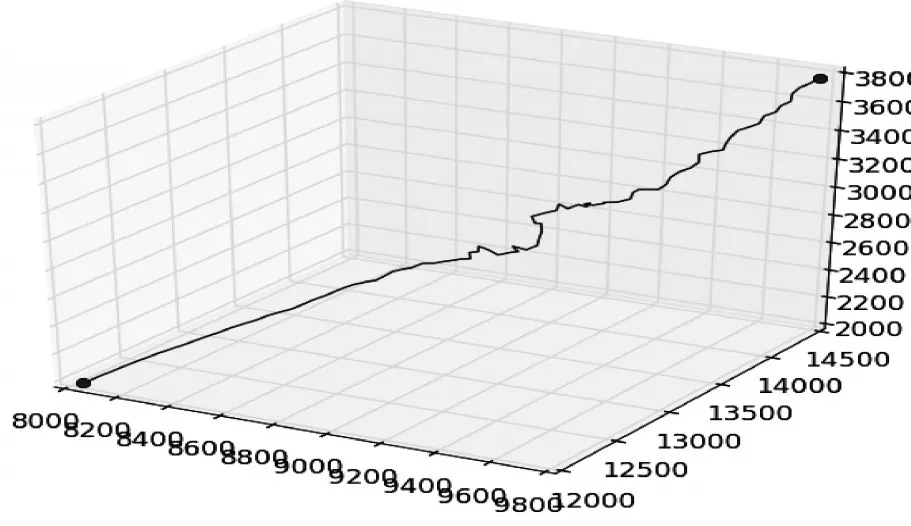
图7 地形遮蔽条件下雷达探测区域图
路径上的探测概率如图8所示。
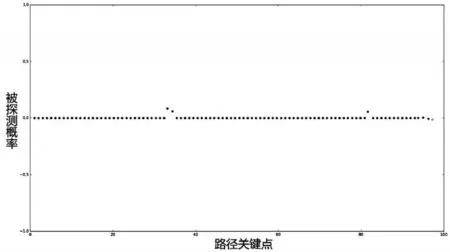
图8 路径关键点与其探测概率
4 结语
论文研究的路径规划方法,可以在有地形遮蔽的雷达探测空间中快速地找出一条路径最短和被探测概率小的航迹。
将模拟退火算法引入RRT中,使得RRT算法有选择低探测空间的能力,从而加强无人机飞行的安全能力。
为使本文提出的算法能真实应用,后期工作将对航迹规划加入更精确的无人机的动力学约束同时也将对算法进行进一步智能优化。

