利用石墨烯进行高地应力测量的仿真研究

张晓平, 张 梦, 刘泉声, 吴顺川, 彭 俊

(1.武汉大学 土木建筑工程学院 岩土与结构工程安全湖北省重点实验室,湖北 武汉 430072;2.昆明理工大学 国土资源学院, 云南 昆明 650093;3.北京科技大学 土木与资源工程学院,北京 100083)

0 引 言

深部地应力测量面临高地温、高应力、高渗透压力的挑战,对深部岩体地应力测量,国内外目前最常采用的两种测量方法是应力解除法和水压致裂法[1]。水压致裂法(hydraulic fracturing)本质上是二维地应力测试方法,该方法假定铅垂方向为一个主应力方向,即自重应力为主应力,这一假定在构造应力显著地区存在严重误差。为此,Cornet F H等人[2]提出了原生裂隙水压致裂法(HTPF)测试来确定地应力,王成虎等人[3]针对该测量方法进行了理论修正,但寻找符合条件的原生裂隙存在极大的困难,制约了该方法的实际应用。采用应力解除法和空心包体应变技术测量时,空心包体应变计受温度影响较大,为此学者研究了相应的温度补偿技术[4]。空心包体应变计的核心为压敏电阻,如将压敏材料进行优化,可得到灵敏度更高、量程更广的的应变计。

单层石墨烯薄膜[5]材料于2004年首次成功制备,随着石墨烯制备方法的不断发展[6],对该材料的研究逐渐增多。石墨烯的理论杨氏模量达1.0 TPa左右,断裂强度为130 GPa左右,最大拉伸应变可达20 %,单层石墨烯薄膜厚度约为0.34 nm。传统MEMS传感器的敏感元件硅的杨氏模量为190 GPa,厚度为微米(μm)级,因此,作为压力敏感材料,石墨烯具有比硅更高的灵敏度以及抗过载能力,而且耐高温(100 ℃以上),可用于深地高地温条件下高灵敏度的动态压力测量。但关于该材料的研究多数为低应力(1 MPa以下)环境下,在高应力环境下的研究较少,为此,本文对在高压环境下石墨烯压力薄膜的相关性质展开研究,为进行深地高地应力测量提供理论依据。

1 理论研究

由于单层石墨烯薄膜的厚度约为0.34 nm,在均布应力作用下其挠度形变远大于薄膜厚度,挠度特性表现为非线性。国内外的相关理论研究如下。

1.1 圆薄膜大挠度模型

1910年冯卡门推导如式(1)所示的平板大挠度非线性方程组[7]

(1)

式中D为圆薄膜的抗弯刚度,E为弹性模量,t为薄膜厚度,r为圆薄膜半径,q为均布载荷,Fr为中面内力,ω为薄膜中心挠度。

对此,钱伟长提出了以荷载和中心挠度为摄动参数的摄动法[8],中心挠度ω与均布载荷q之间的关系

(2)

式中ν为泊松比,其余符号同上。

应用里茨法求解圆薄膜问题时[9],中心挠度ω表示为

(3)

1.2 球壳模型

1959年Beams J W通过鼓泡实验获取沉积在基体上的薄膜力学性能,提出了相应的球壳模型[10],考虑薄膜预应力的影响时,其挠度特性为

(4)

式中σ0为石墨烯薄膜的预应力。

1.3 Ma J模型

2012年香港理工大学Ma J等人制作了光纤F-P腔石墨烯压力传感器以实验分析石墨烯薄膜的力学性能[13],给出了均布荷载q与薄膜挠度ω之间的近似关系

(5)

2 石墨烯薄膜的有限元仿真模拟

在理论模型的基础上,利用COMSOL软件,构建了石墨烯薄膜挠度特性的仿真模型。以直径为5 000 nm的单层石墨烯圆薄膜为分析对象,周边边界条件为固支,石墨烯材料的弹性模量E、预应力σ0、厚度t、泊松比ν分别为1 TPa,1.0 GPa,0.34 nm和0.16,考虑到预应力效果,设置模型的初始预应力为0.1 N/m。由于单层石墨烯很薄,在均布应力作用下会产生非线性变形,因此,COMSOL中选用二维板结构,并在计算时,选取几何非线性。在0.1～1 MPa的载荷范围内以0.05 MPa为间隔,在1～5 MPa的载荷范围内以0.5 MPa为间隔,一共选取27组均布应力分别施加于石墨烯圆薄膜上。

在实际测量时,仪器所测的应力是根据位移计算得出,因此,比较在相同位移下COMSOL值与理论值的误差。根据COMSOL的位移结果,计算各个理论相对应的应力值,比较与COMSOL施加应力值的误差,其结果如图1所示。

图1 在0.1～5 MPa应力范围内仿真结果

由图1(a)可知,Beams方程解与仿真解最接近,且随着石墨烯薄膜的变形越来越大,其余方法的解与COMSOL仿真值的绝对误差越来也大。由图1(b)可知,在图中应力范围内,Beams方程解与COMSOL值的相对误差先减小后增大,当均布应力为0.1 MPa时相对误差为最大值7.53 %,当均布应力为0.95 MPa时相对误差为最小值-0.01 %。而其余方法计算的结果与COMSOL值的相对误差随着应力的增大越来越小。三阶摄动解与COMSOL值的相对误差由13.12 %减小至4.06 %;变分法与COMSOL值的相对误差由28.37 %减小至18.07 %;Ma J模型与COMSOL值的相对误差由-43.27 %减小至31.91 %。

为了分析高应力条件下的力学响应,增大在COMSOL施加的应力,在5～100 MPa载荷范围内以5 MPa间隔,一共选取20组均布应力施加于石墨烯薄膜上(暂不考虑石墨烯的破坏),并进行误差计算。其结果如图2所示。

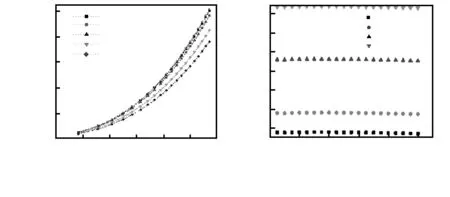
图2 在5～100 MPa应力范围内仿真结果

由图2可知,高应力条件下,Beams方程解与COMSOL施加的应力值误差最小,且随应力的增大,Beams方程解与COMSOL值的相对误差趋势为先减小后增大,最大相对误差为1.32 %(应力为100 MPa),最小相对误差为0.93 %(应力为35 MPa),相对误差均值为1.06 %,而其余解与COMSOL值的相对误差趋势为逐渐减小,但其余解的相对误差相比Beams方程解的相对误差太大。而Beams鼓泡试验曾用来研究石墨烯的纳米力学性质[11,12],因此Beams理论更适合用来描述石墨烯的变形特性,而薄板模型的弯曲刚度较大,其不适合解释石墨烯薄膜压力敏感特性。由上述模拟结果可知,在低压下的COMSOL值与Beams方程解的绝对误差很小,其相对误差随着压强的增大先减小后增大,在0.95 MPa时的绝对误差为最小值-0.000 1 MPa,在100 MPa时的绝对误差为最大值-1.3406 MPa,高应力条件下绝对误差增大很多,会带来测量精度的下降。但相对误差增加有限,100 MPa时的相对误差也只有1.32 %,能满足测量的需要。COMSOL值与其余理论解的绝对误差随着压强的增大逐渐增大,且绝对误差都比Beams方程解大。

结合上述计算结果可知,COMSOL值与Beams方程解的误差很小,因此,COMSOL可以用来模拟计算单层石墨烯薄膜在均布应力下的变形特性。而石墨烯薄膜的压力敏感特性还与薄膜厚度有关,为进一步验证COMSOL模拟的有效性,分别以1,2,3,4,5,6,7层石墨烯薄膜为研究对象,仿真分析在上述20组(5～100 MPa)均布载荷作用下不同薄膜厚度的中心挠度位移特性,如图3所示。

图3 不同位移与厚度下的均布应力

由图3可知,在不同薄膜厚度下,COMSOL应力值与Beams方程解的误差很小(1 %左右)。因此,在不同薄膜厚度下,COMSOL软件仍然可用于模拟计算石墨烯薄膜受均布应力下的变形特性。因为上述研究并没有考虑在高应力下,石墨烯薄膜是否会导致断裂,因此,对高应力下的石墨烯薄膜进行变形和受力分析。

周边固支的圆形石墨烯薄膜在均布应力(施加在z方向上)下的变形示意图如图4所示,在石墨烯薄膜中心处的挠度最大。

图4 石墨烯薄膜示变形示意图

计算在图4(b)中下弧线的长度,即石墨烯薄膜变形后的线长,可据此计算石墨烯薄膜的应变。对1,2,3,4,5,6,7层石墨烯分别施加范围为5～100 MPa,间隔为5 MPa的均布应力,计算不同层石墨烯薄膜在不同应力下的应变,如图5(a)所示。由图可知,随着石墨烯层数的增加,相同应力下石墨烯薄膜的应变越来越小,且应变减小的幅度也逐渐变小,而1层石墨烯薄膜对均布应力的灵敏度远高其他层石墨烯薄膜。在90 MPa的均布应力下,1层石墨烯的应变为19.918 %,在95 MPa均布应力下,1层石墨烯的应变为20.542 %,而其它层石墨烯在100 MPa内的应变均不超过20 %。

在均布应力下,不同层石墨烯薄膜在均布应力下的最大应力如图5(b)所示。已知石墨烯的最大抗拉强度为130 GPa左右,结合图5可知,1层石墨烯能承受的最大均布应力值在25～30 MPa之间,2层石墨烯能承受的最大均布应力值在55～60 MPa之间,3层石墨烯能承受的最大均布应力值在80～85 MPa之间,而4,5,6,7层石墨烯能承受的最大均布应力值均超过了100 MPa。

图5 不同层石墨烯下的应变和最大应力

结合图1(a)、图2(a)、图3可知,在石墨烯薄膜未破坏时,COMSOL软件可以很好地对石墨烯薄膜进行均布应力下变形及受力的模拟分析。可以根据待测应力值的范围,选定合适层数的石墨烯薄膜,在满足量程要求的情况下,尽可能提高测量的灵敏度。

3 采用石墨烯薄膜进行深部高地应力测量的讨论

在不同均布应力下,石墨烯薄膜会产生相应的变形,导致其压阻发生改变,即压阻效应,可以利用该特性进行应力测量。

已有实验通过不同方法研究了石墨烯薄膜的压阻性质并测量其应变系数,Huang M等人[14]利用纳米压痕实验对受压悬浮石墨烯纳米带进行电学测试,测得的应变系数为1.9。Smith A D等人[15]对固支在矩形空腔上方的石墨烯薄膜加压使其发生形变,得到应变系数的平均值为2.92。Fu X W的课题组[16]研究发现,转移到聚二甲基硅氧烷(PDMS)基底上的石墨烯应变系数高达151。Lee Y等人[17]将石墨烯转移到PDMS基底,测得的应变系数约为6.1;同样是该课题组[18],制作了夹角为120°的石墨烯应变传感器,当应变小于1.8 %时,应变系数为2.4,当应变在1.8 %～7.1 %范围内时,应变系数的范围为4～14,当应变大于7.1 %时,传感器失效破坏。上述试验所得的应变系数不完全一致,因此很难说石墨烯电阻的变化完全是因为自身的结构形变,尚需要更深入的研究去解释这一现象。

在已知石墨烯薄膜压阻效应的基础上,利用仿真软件对其进行模拟分析,可为石墨烯应变传感器的提供设计依据。

4 结 论

本文列举了可用于分析石墨烯薄膜的理论模型,其中球壳模型被广泛应用。对于大应力下的石墨烯薄膜变形,利用COMSOL进行仿真分析,在不考虑石墨烯薄膜是否破坏的情况下,将其结果与各理论进行对比,发现仿真结果与球壳模型的结果最为接近,高压下的绝对误差比低压下的绝对误差大,会带来测量精度的下降,但在高压下的相对误差较小,误差范围在1 %左右,能满足应力测量的要求。在此基础上利用COMSOL软件对石墨烯薄膜的应变与应力进行模拟计算,讨论不同层石墨烯薄膜在该压强范围内是否破坏,将讨论结果与上述误差结果进行结合,共同验证了在较大压强下且石墨烯未破坏时,利用COMSOL软件模拟的可靠性,同时计算给出根据待测应力值的范围,选定合适层数的石墨烯薄膜,在满足量程要求的情况下,尽可能提高测量的灵敏度。