极端环境下光电编码器误差补偿方法*

王 慧， 郭成虎

(辽宁工程技术大学 机械工程学院，辽宁 阜新 123000)

0 引 言

光电编码器是用于测量旋转机构角度的仪器，其优点是测量精度高、体积小巧、可靠性好，因此在航天、高精度加工、机器人以及高精度测量领域得到非常广泛的应用。随着技术的不断发展，人们对测量的精度要求不断提升，因此对于高精度光电编码器的需求日益增长[1～3]。

周良杰等人[4]从磁场分布特性、结构特性与装配特性三方面入手，研究用于方向盘转角测量传感器的角度误差补偿方法。王艳永等人[5]提出了一种基于改进的ANFIS系统的角度传感器误差补偿方法，通过试验验证了提出方法的可行性。张倩[6]针对光电编码器精度检测、误差来源和误差补偿方法进行系统的研究。于海[7]对传感器误差测试检测方法展开了研究，提出了动态误差理论，对影响光电编码器动态误差的多种因素进行深入分析。冯英翘[8]对因莫尔条纹信号质量产生的光电编码器测量误差进行深入研究，提出改进光电编码器分辨力和精度的有效手段。顾伯忠等人[9]针对用于高精度跟踪望远镜上的轴角反馈元件高精度的光电编码器在-50 ℃这样极端低温的环境下的跟踪精度进行了测试，研究了温度效应对光电编码器的影响。

高、低温的极端环境会对光电编码器性能带来非常大的影响，限制了其在高、低温的应用与发展。本文在前人研究基础上，针对高、低温环境对光电编码器的影响以及高、低温环境下传感器的误差补偿方法进行研究。

1 光电编码器工作原理

光电编码器工作原理图如图1所示，主要由主轴、发光管、码盘、狭缝、接收管和数据处理电路组成。光电编码器运行时，狭缝不动，码盘在主轴带动下旋转，码盘与狭缝的相对位置变化产生了莫尔条纹。发光管与接收管之间的配合完成了由机械位置变化信号到光信号的转换。再由光电接收器完成光电信号的转换，再经过处理电路转换成表示旋转角度信息的代码[7]。

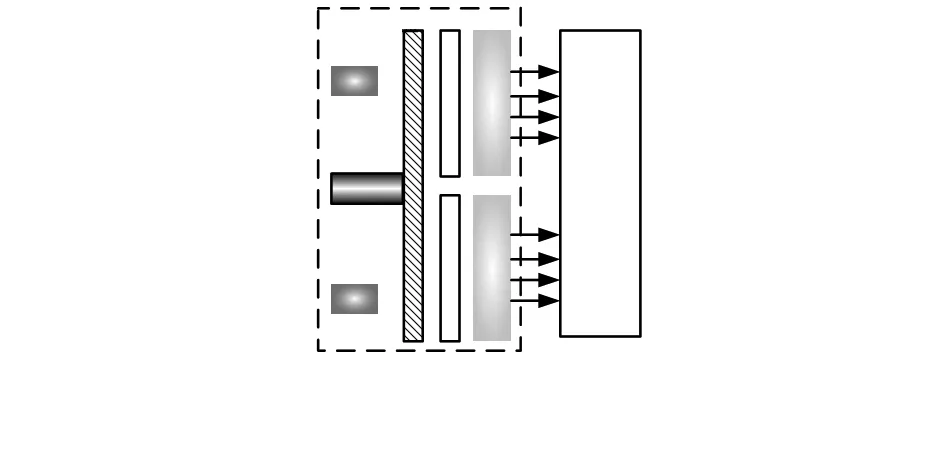
图1 光电编码器工作原理

光电编码器采用矩阵编码方式的码盘结构。通常情况下，光电编码器的码盘有五圈同心的圆码道。由透光和不透光扇形图案布置在各个圆码道上，如图2所示。

图2 码道关系

C1～C4为4个由256 对线/周的光栅码的精码道。该码道决定了编码器的精度。A9为用于精码对粗码的校正的校正码道。A1～A8为采用矩阵编码的粗码道。该码道的作用是缩小了码盘直径，实现了编码器小型化[7]。

2 极端环境下光电编码器误差检测

本文通过可调温的测试系统研究高温、低温环境对光电编码器的测量精度的影响，可调温的测试系统简图如图3所示。

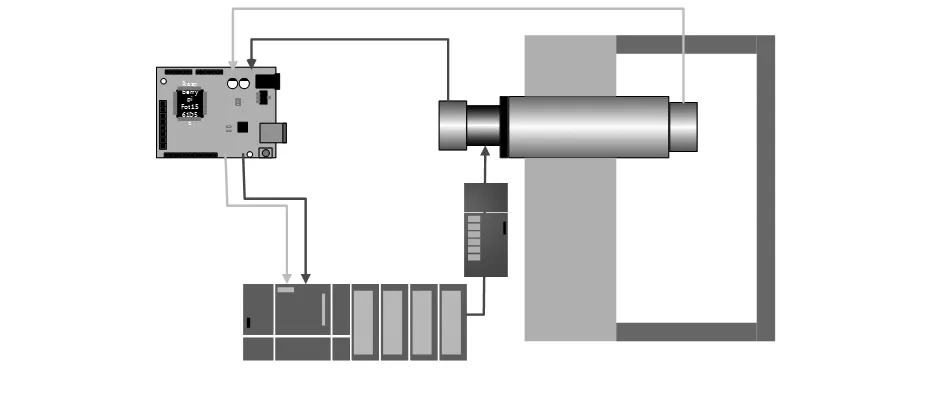
图3 极端环境下光电编码器误差检测试验装置

该测试系统主要包括基准编码器、被测光电编码器、可调温密封箱、隔热连接轴、数据采集处理系统等。

本文以标准偏差σ作为光电编码器的测量误差的衡量标准，标准偏差σ可以表示为

(1)

通过可调温的测试系统测得不同温度下，被测光电编码器的测量误差。图4为高温、常温以及低温环境下被测光电编码器在一个整周上每次转过一个角度后的测量误差，单位为(′)。

图5为从低温至高温环境下被测光电编码器的测量误差的平均误差曲线。

图5 被测光电编码器的测量误差的平均误差曲线

可以看出，高温及低温的极端环境会对光电编码器性能带来非常大的影响，并且在高温及低温区，测量误差呈非线性，而在常温区测量误差呈线性。

3 光电编码器误差补偿方法

3.1 光电编码器误差补偿方法框架构建

光电编码器在高温及低温区，测量误差呈非线性，而在常温区测量误差呈线性。本文构建如图6所示的光电编码器误差补偿方法框架。

图6 光电编码器误差补偿方法框架

由如图6所示的光电编码器误差补偿方法框架可知，该补偿方法通过温度判别光电编码器所处环境分区，并切换不同的补偿方法实现经济高效的误差补偿。对于常温区呈线性的测量误差，采用直线最小二乘法补偿模型，而对于高温及低温区呈非线性的测量误差，采用处理非线性拟合更优的补偿模型[10]。在此使用最小二乘支持向量机(least squares support vector machine，LS-SVM)模型实现非线性区的误差补偿，LS-SVM模型能够把误差补偿的二次优化问题简化成为线性方程组的求解问题，较好地解决了光电编码器小样本、非线性及容易陷入局部极小值等神经网络模型带来的问题，在不损失较高的拟合精度下，降低误差补偿的计算复杂性[11]。

3.2 线性区误差补偿算法

使用直线方程对光电编码器进行常温区下的误差补偿

y=α+βx+e

(2)

(3)

(4)

式中α为常数项；β为系数；e为为拟合的光电编码器误差。

在使用直线拟合方程进行传感器误差拟合时，为了使得直线拟合的区间覆盖尽可能大的范围，从而提高整体光电编码器误差补偿的效率，降低计算复杂度，需要根据传感器精度要求，自动搜寻常温区域的线性段。方法如下:令初始直线拟合的区间为[t1,t2]= [t0,t1]，对该初始区间进行直线拟合误差补偿，得到拟合误差的最大值emax若大于事先设定的误差最小值，那么可更新区间t1=t1+τ，对更新后的拟合区间再次进行直线拟合，得到新的拟合误差的最大值emax如果还是大于设定误差最小值，则再次更新区间t2=t2-τ，对更新后的区间再次进行直线拟合，直到拟合误差的最大值emax不高于设定误差最小值即可[10]。

3.3 非线性区误差补偿算法

设定光电编码器误差补偿模型的训练样本为：{(xi,yi)|xi∈Rn,i=1,2,…，l}，其中，l为光电编码器误差补偿模型的训练样本数量，xi为误差补偿模型的输入向量，yi为误差补偿模型的输出。 在高维特征空间H中，误差补偿的样本集合表示为如下映射关系

y(x)=<ωφ(x)>+b

(5)

通过松弛因子ζ和ζ*确保光电编码器误差补偿模型线性拟合得到的拟合误差实现最小化

(6)

其约束条件表示

(7)

LS-SVM的提出是利用正则化原理，通过最小二乘函数和等式约束将上两式转换为

(8)

yi[ωTφ(xi)+b]=1-ei

(9)

通过对约束条件进行求偏导得

(10)

对求偏导后的约束条件进行回归函数求解

(11)

在确定参数的过程中常规LSSVM识别模型所选取的网络搜索法耗时较长，在搜索的时候只能够针对网格点进行，所以,当不具有较为恰当的网格大小时就无法保证参数的有效性。LSSVM识别模型的优化可以借助粒子群优化算法来实现。这种算法不会受到函数约束条件的局限，搜索可以借助个体适配信息来实现，保证具有较强的全局优化能力。对于多维以及复杂的实际问题，因为种群中多样性逐渐的降低，使得早熟收敛问题在算法中容易出现，对于全局寻优能力产生不利的影响[12]。使用文献[13]中的方法对算法进行优化。

通过终止条件判别是否结束优化算法[14，15]。对高低温非线性区使用LSSVM模型进行光电编码器误差补偿方法如图7所示。

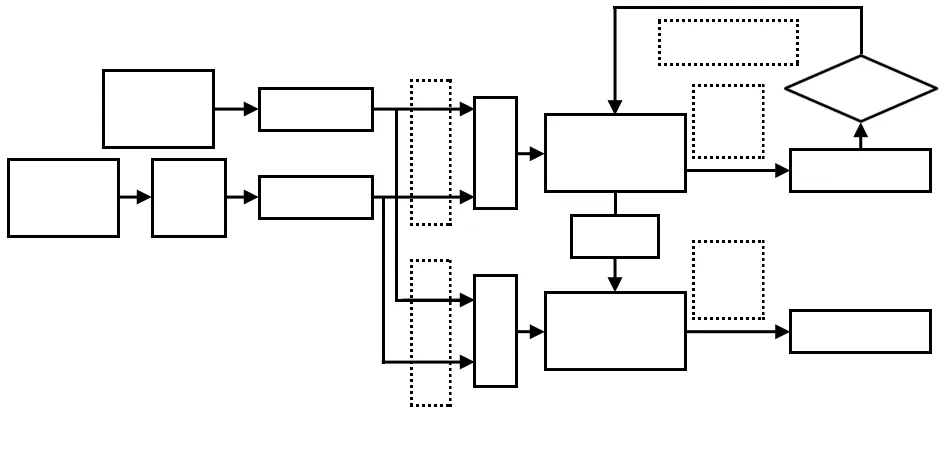
图7 极端环境下光电编码器误差补偿方法

4 极端环境下光电编码器误差补偿实验

下面通过实验方法对本文研究的极端环境下光电编码器误差补偿方法的可行性进行验证。

通过可调温的测试系统测得不同温度下，被测光电编码器的测量误差。图8为高温以及低温环境下被测光电编码器在一个整周上每次转过一个角度后的测量误差。

图8 高、低温环境下被测光电编码器的测量误差

实验结果表明：通过本文研究的极端环境下光电编码器误差补偿方法，可有效降低传感器在高温和低温环境下的测量误差。

通过3种实验方法，对比验证本文研究的极端环境下光电编码器误差补偿方法的优势。

方法1在全温度范围内均使用基于直线最小二乘法的光电编码器误差补偿模型。

方法2在全温度范围内均使用基于常规LSSVM模型的光电编码器误差补偿模型。

方法3使用本文研究的极端环境下光电编码器误差补偿方法。

得到如图9所示的3种实验方法下的测量误差。

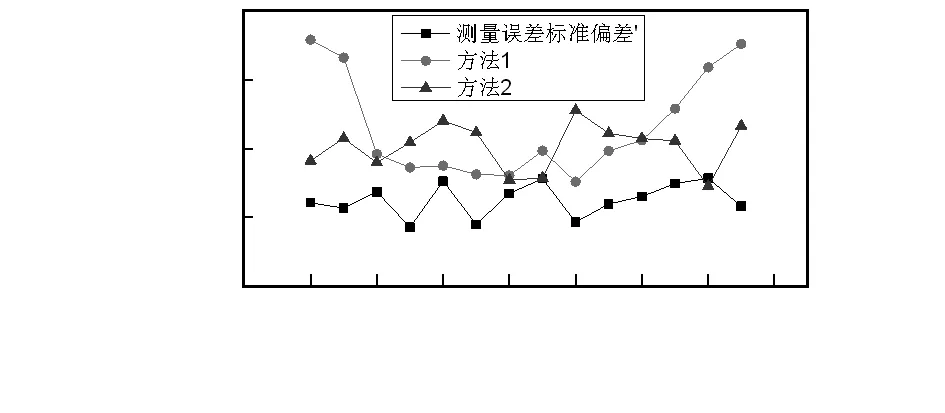
图9 3种实验方法下的测量误差

实验结果表明，常规的直线最小二乘法误差补偿模型对于光电编码器在常温区域内产生的误差有较好的补偿作用，而在高温和低温区对光电编码器的测量误差补偿效果不佳，不难满足使用要求，在低温区测量误差的标准偏差均值为11.5′，而在高温区测量误差的标准偏差均值为21.2′，在低温区测量误差的标准偏差均值为20.9′。

常规LSSVM模型建立的误差补偿模型和本文研究的极端环境下光电编码器误差补偿方法不仅对常温区域内产生的误差有较好的补偿作用，而且对高温和低温区呈非线性变化的测量误差也有很好的补偿作用，全温度范围内测量误差的标准偏差均值为15.3′。另外由于本文研究的极端环境下光电编码器误差补偿方法中对LSSVM模型进行了优化，使得光电编码器的测量精度更高，全温度范围内测量误差的标准偏差均值为11.4′，相比未进行补偿前的测量误差降低64.1 %。

5 结 论

1)通过可调温的实验装置测试得出高温及低温的极端环境会对光电编码器性能带来非常大的影响，并且在高温及低温区，测量误差呈非线性，而在常温区测量误差呈线性。

2)建立光电编码器误差补偿方法，通过温度判别光电编码器所处环境分区，并切换不同的补偿方法实现经济高效的误差补偿。

3)实验验证本文研究的极端环境下光电编码器误差补偿方法无论对常温区域内还是对高温和低温区呈非线性变化的测量误差均有很好的补偿作用。另外由于本文研究的极端环境下光电编码器误差补偿方法中对LSSVM模型进行了优化，使得光电编码器的测量精度更高。