浮式液化天然气系统液体装载船体的耦合响应
赵东亚,胡志强,陈 刚,3
(1.上海交通大学 海洋工程国家重点实验室,上海 200240;2.纽卡斯尔大学 工程学院, 英国 纽卡斯尔 NE1 7RU;3.中国船舶及海洋工程设计研究院,上海 200011)
作为一种清洁能源,天然气在解决能源需求和减小碳排放方面具有独特的优势.海上浮式液化天然气(FLNG)生产平台是一种新的天然气开发方式,具有在远海进行天然气处理、液化、储存功能[1].在开采和卸载作业中FLNG和天然气运输船LNGC(LNG Carrier)均受到内部液舱晃荡引起的载荷,且FLNG和LNGC内的液舱装载处于动态变化的状态.因此,准确、快速地预报液舱装载船体的耦合响应十分必要.
将船体运动和液舱晃荡进行线性化处理后,可以在频域内快速实现液体装载船体的耦合计算,获得液体装载船舶的耦合响应特性,文献[2]采用频域数值方法研究了晃荡对船体运动的影响.当液舱装载较浅或船体运动幅值增加时,液舱晃荡会呈现出明显的非线性特性.在时域内将船舶运动与非线性晃荡迭代求解可以获得更为准确的结果.在计算船体响应时,基于线性波浪理论,采用脉冲响应方法可以实现在时域内快速求解[3].在计算内部液舱晃荡时,采用计算流体力学(CFD)方法可以对晃荡剧烈的工况进行计算.文献 [4-5] 采用CFD程序SOLA计算液体装载船体的耦合响应,并开展模型试验以验证数值计算的有效性.文献[6]采用Openfoam预报晃荡响应,根据脉冲响应理论(IRF)计算船体运动响应,而后在时域内进行迭代求解;通过对比不同波浪幅值下的船体运动响应发现,大幅值波浪激励下液舱晃荡更为剧烈,但晃荡冲击载荷对船体运动响应影响很小.由于CFD方法计算耗时,在处理FLNG这种具有多个大型液舱,且载况较多的工况时,计算效率很低.因此,在处理晃荡程度较低的工况时可以采用势流方法以提高计算效率.文献 [7-9] 通过数值和试验的方法研究了液体装载液舱在波浪中的响应,假设舱内晃荡流体有势,采用边界元法(BEM)进行数值求解.但是这些研究或是将液舱简化为二维液舱,或是仅考虑部分运动模态与液舱晃荡的耦合作用,不能全面预报船体6自由度运动与内部液舱晃荡的耦合响应.此外,针对液舱晃荡和船体运动耦合作用机理的研究也十分有限.
本文对FLNG系统中液体装载船体的耦合响应进行研究.在数值计算中采用基于IRF的方法进行船体运动求解,采用势流理论结合黏性阻尼的方式对液舱晃荡进行预报,建立一套时域耦合预报程序以实现船体6自由度运动与液舱晃荡的耦合计算.在上海交通大学海洋深水试验池开展模型试验研究,对数值模拟程序的准确性进行验证.基于数值计算和试验结果研究了不同船体运动模态与内部液舱晃荡的耦合机理,同时分析了不同液舱布置方式对耦合响应的影响.
1 数学模型
本文考虑带有2个矩形液舱的船体模型,两液舱相对船中剖面对称分布.坐标系定义如图 1所示.图中:O-XYZ为大地坐标系,随船坐标系o-xyz的原点位于船体水线面中心处,x轴、y轴和z轴分别指向船首、左舷和垂直向上.在初始状态,坐标系o-xyz与O-XYZ重合.o1-x1y1z1和o2-x2y2z2分别为液舱1和液舱2的随体坐标系,其原点位于液舱静水面中心处,且与随船坐标系o-xyz平行.
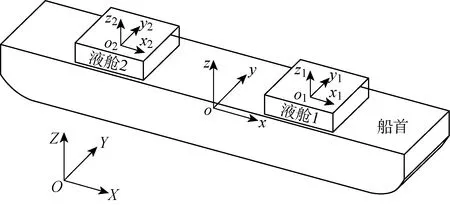
图1 液体装载FLNG船体坐标系Fig.1 Coordinate systems of FLNG vessel with two liquid tanks
1.1 船体运动求解
对于大型海洋结构物,可采用线性波浪理论.不考虑船体航速时,微幅线性规则波入射势可表示为
φI(x,y,z,t)=
(1)
式中:A、ω、k、θ和σ分别为入射波波幅、圆频率、波数、浪向和相位;g为重力加速度;t为时间.
将流场速度势分离出绕射势与辐射势,在频域内求解速度势的边值问题可以获得辐射势对应的浮体附加质量和势流阻尼系数[10].基于IRF可获得时域内的船体运动方程:
Cijxj(t)=Fwj(t),i,j=1,2,…,6
(2)
式中:Mij、μij、kij和Cij分别为不同模态下的船体总质量、附加质量、时延函数及静水回复力系数;Fwj为船体受到的波浪载荷.时延函数反映了水体的记忆效应,由频域中的浮体势流阻尼系数积分可得
(3)
式中:λij为频域内的浮体阻尼系数.在船体横摇运动计算中需考虑黏性阻尼的作用,在数值模型中采用线性阻尼模型替代:
(4)
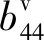
1.2 液舱晃荡求解
本文给出了液舱内部晃荡在随体坐标系下的数学描述.图2所示为矩形液舱1示意图.图中:B、W和D分别为液舱长、宽和舱内水深.液舱1和液舱2的计算方法相同,本文用o-xyz代替o1-x1y1z1或o2-x2y2z2.在外界激励下,液舱在大地坐标系下的运动可以表示为
V=[uvw]=d[dx(t)dy(t)dz(t)]/dt
(5)
ω=d[θx(t)θy(t)θz(t)]/dt
(6)
式中:d=[dx(t)dy(t)dz(t)],θ=[θx(t)θy(t)θz(t)]分别代表液舱的平动和转动.
假设流体为无黏、无旋以及不可压缩的流体,则流体的流动可用势函数φ表示.在随体坐标系中将速度势进行φ=φ+xu+yv+zw的分解,以消除速度势中的水平激励部分.在流场内速度势φ满足 Laplace 方程:
(7)
在壁面处满足旋转激励边界条件:
∂φ/∂n=ω×r·n
(8)
式中:n为壁面法向量;r为旋转中心到边界节点的矢量.自由面处运动学和动力学条件:
(9)
(10)
式中:g=[0 0 -g]T;r0=[xyζ]T,ζ为自由面幅值;kθ为发生旋转时两坐标系间的矢量转换关系,
(11)
α、β、γ为绕x、y、z轴旋转的角度.在初始时刻液舱处于平衡位置,液面处于静止状态.速度势和自由面初始条件为φ(x,y,0)=0和ζ(x,y,0)=0.
求解以上边值问题后可得边界处的速度势和法向速度势.根据伯努利方程可得壁面处压力分布:
(12)
至此,某一时刻的流场域已求解完毕.本文为方便在时域内对网格进行更新,仅在z轴方向进行自由面步进.速度势和自由面升高的步进公式为
(13)
(14)
在模型中引入Rayleigh阻尼模型来考虑真实晃荡中存在的黏性作用.阻尼模型在自由面表面施加一个与流体质点运动方向相反、与速度呈线性关系的阻尼力.给定μ为阻尼系数,修正后的自由面动力学方程:
(15)
采用边界元法对上述边值问题进行求解.数值离散与方程求解过程详见文献 [11],此处不再赘述.
1.3 船体运动与晃荡耦合计算
在时域内求解液体装载的船体运动耦合响应时,需将液舱晃荡与波浪中的船体运动响应耦合求解.在耦合过程中:船体的运动作为液舱的外部激励作用在舱壁上,即晃荡求解问题中的边界条件;同时液舱晃荡载荷作为外载荷作用在船体上.将晃荡载荷Fs作为船体运动的外载荷,则式(2)变为
Fwj(t)+Fsj(t)i,j=1,2,…,6
(16)
式中:ξj和Fsj分别为船体运动和船体受到的液舱晃荡载荷.
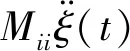

图3 液舱晃荡与船体运动耦合求解流程图Fig.3 Flow chart of coupled vessel motion and internal sloshing calculation
2 模型试验
在上海交通大学海洋深水试验池开展模型试验,研究液体装载船体的耦合响应.图4所示为FLNG船体型线和液舱安装位置.图中:Ti(i=1,2,…,5)为浪高仪位置,以测量舱内晃荡波面.
20世纪70年代末期,随着改革开放政策的推行,中国大陆社会进入了一个新的历史时期。伴随着商品经济的迅速发展,录音机、音像制品开始走进大众的日常生活,港台流行音乐迅速风靡。以邓丽君、刘文正、徐小凤、张帝等为代表的港台流行歌手,其歌曲为大陆民众所喜爱并广为传唱。[14]1其中,尤以邓丽君的流行歌曲传播最多、最广。[15]182港台流行音乐进入大陆,不仅迅速改变并丰富了原有的大众音乐文化构成,同时也成为大陆流行音乐文化最初的范本,对日后大陆流行音乐的发展产生了深远影响。
表1所示为FLNG船型、液舱的主要参数及固体装载时的惯量参数.液体装载时液舱采用淡水装载.当假设流体不能流动时,液体装载的惯量参数与固体装载工况一致.模型试验采用1∶60的缩尺比.

图4 带2个矩形液舱的FLNG船型(m)Fig.4 Profiles of FLNG vessel with two rectangular tanks (m)
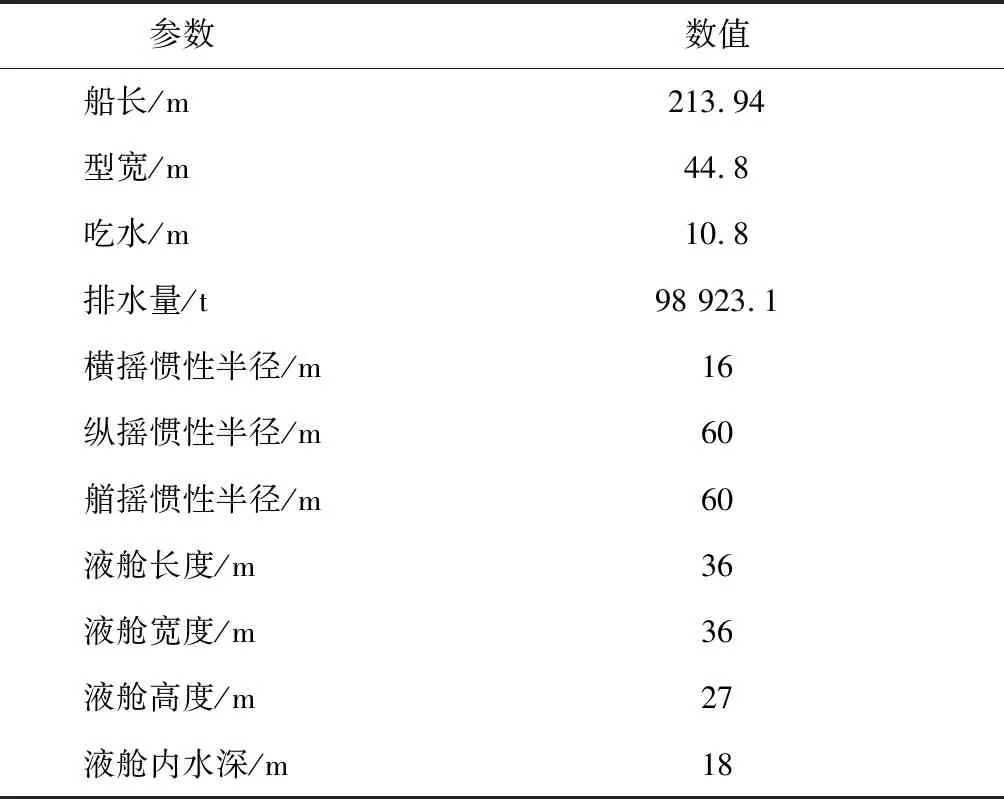
表1 FLNG船体与液舱主要参数Tab.1 Main particulars of FLNG vessel and LNG tanks
海洋工程深水池长、宽和最大水深尺寸分别为50、40和10 m,其中相邻两侧安装有造波板,另外相邻两侧为消波滩.模型在水池中的布置如图5所示.船体采用水平系泊固定以消除二阶波浪力引起的慢漂运动,同时水平系泊刚度保证其固有周期远大于船体的主要响应周期.试验中采用白噪声波浪,波浪周期覆盖主要的船体运动和晃荡响应周期.图 6所示为横浪时白噪声校波结果与目标值的对比.由图可见,造波精度满足试验要求.根据波浪谱Sx(ω)和对应海况下的船体运动或晃荡响应谱Sy(ω)即可求得对应物理量的幅值响应函数(RAO):
(17)
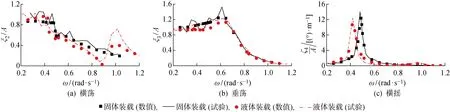
图8 横浪场景下固、液装载船体运动响应RAOFig.8 RAOs of vessel motions in solid and liquid loading condition under beam sea
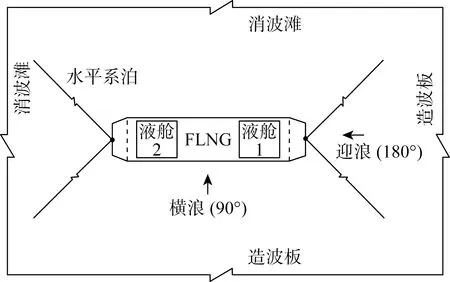
图5 模型在水池中的水平系泊布置Fig.5 Arrangement of vessel model in water basin
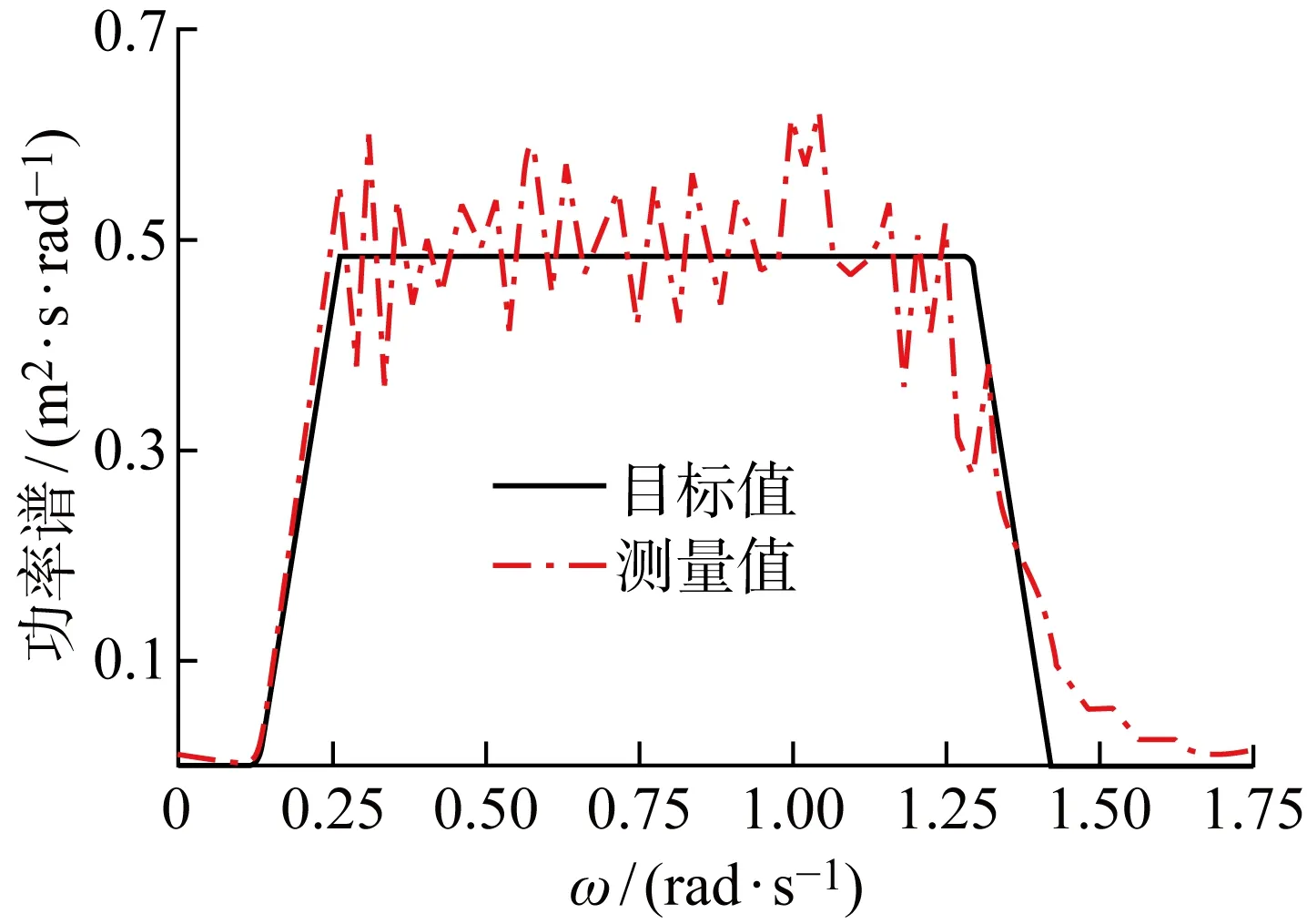
图6 横浪白噪声功率谱Fig.6 Spectra of white noise wave in beam sea condition
3 数值模拟程序验证
3.1 液舱晃荡程序验证
将图 2中的液舱尺寸根据水深无量纲化后,晃荡的固有频率为
ωmn=
(18)
式中:m、n为沿B、W方向的晃荡模态阶数.
根据文献[12]中采用有限元法计算的三维液舱晃荡结果对数值模拟程序的有效性进行验证.在验证工况中,依据水深D进行无量纲化后,液舱参数B=W=4,液舱同时受到x和y向的水平正弦激励:Ax=0.037 2,ωx=ω10,Ay=0.018 2,ωy=ω01.保证计算收敛的情况下选择网格数为 14×14×5,时间步长为Δτ=0.018 8.图 7所示为自由面角点(B/2,W/2)和(B/2,-W/2)处的波面升高时历对比结果.可以看出,本数值模拟程序可以获得准确的三维晃荡计算结果.
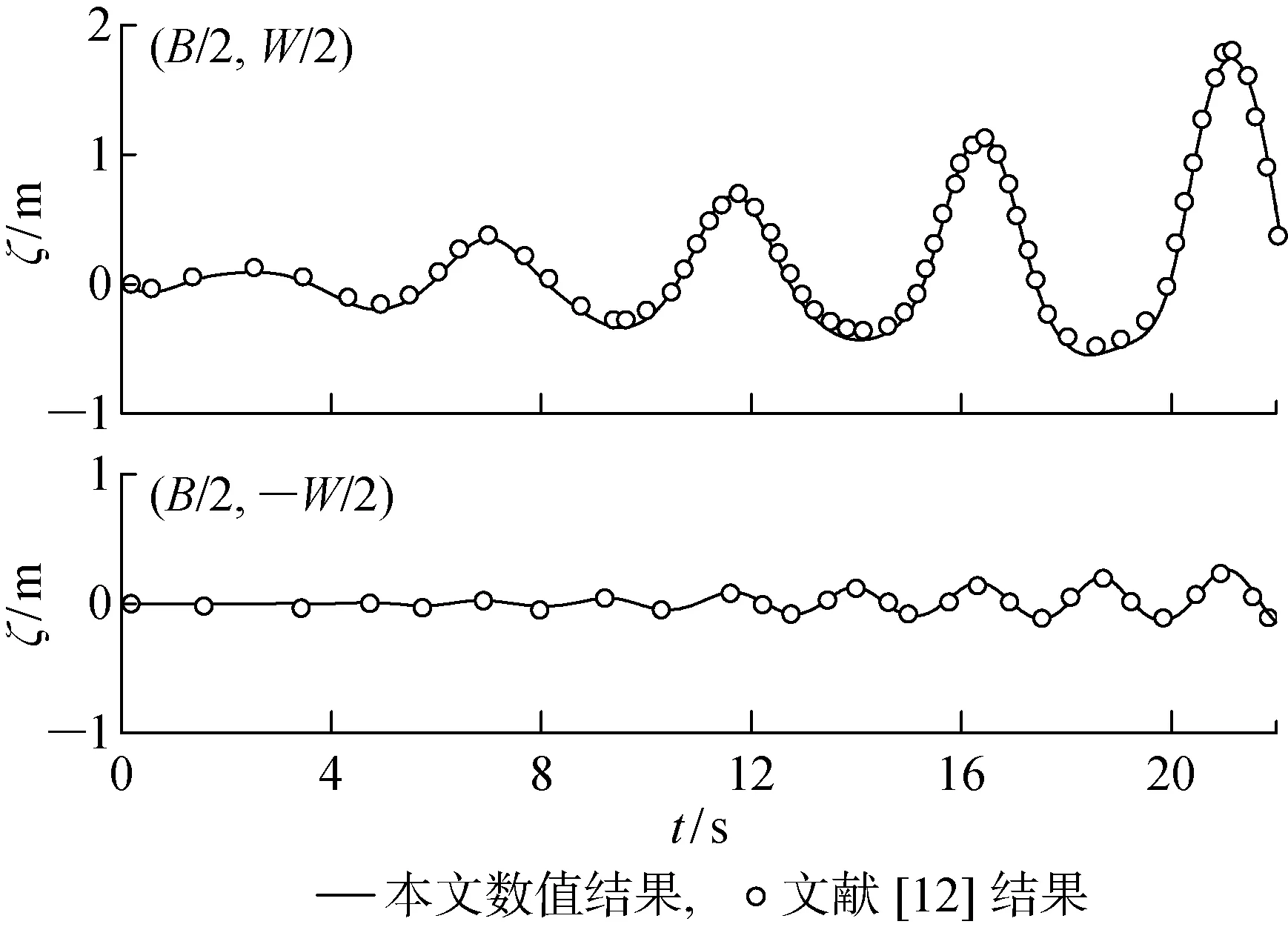
图7 水平激励下的晃荡时历验证Fig.7 Wave elevation histories due to transitional excitation
3.2 液体装载船体耦合计算验证
在数值计算中选择液舱自由面阻尼系数μ=0.1[11].图8所示为固体和液体载况下船体在横浪场景下的运动响应RAO.可以看出,数值结果和试验结果吻合较好.这说明本数值模拟程序在计算船体运动以及液体装载船体耦合响应时可以获得准确的结果.但在横摇固有频率ωr处黏性阻尼将呈现出显著的非线性特性,线性阻尼模型不再适用,进而影响横摇峰值的计算精度.
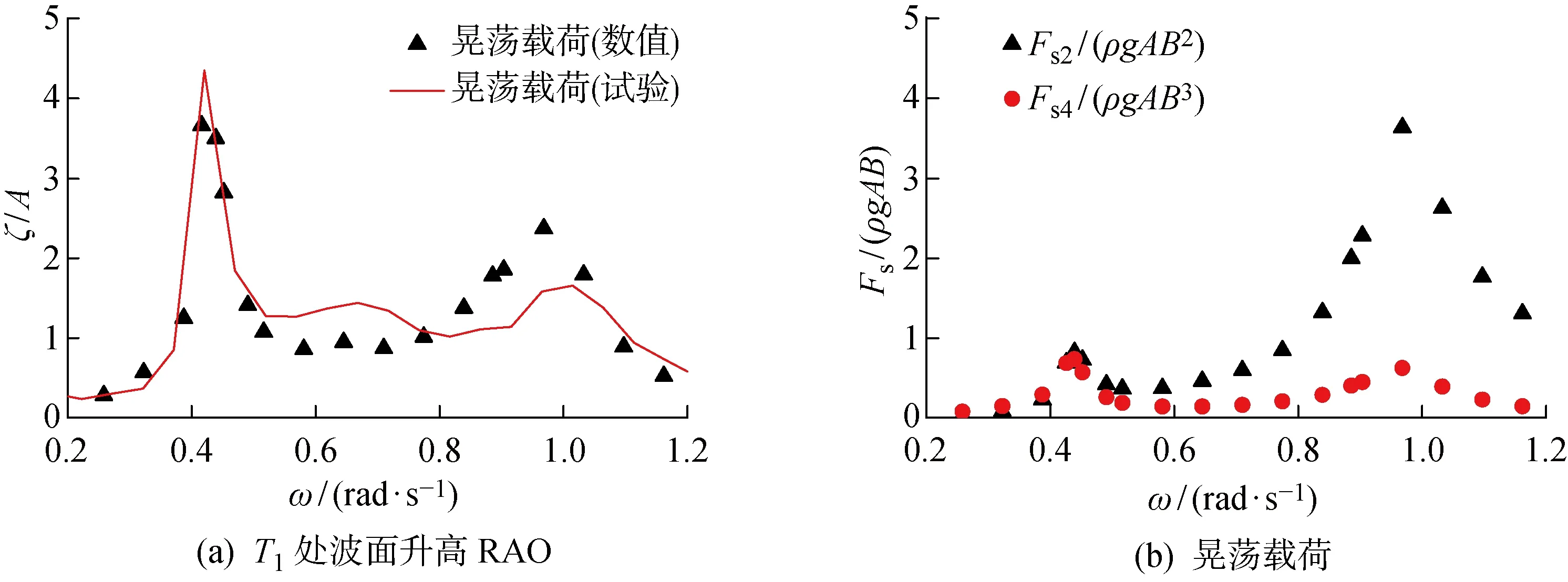
图9 横浪下的晃荡响应Fig.9 Sloshing responses under beam sea
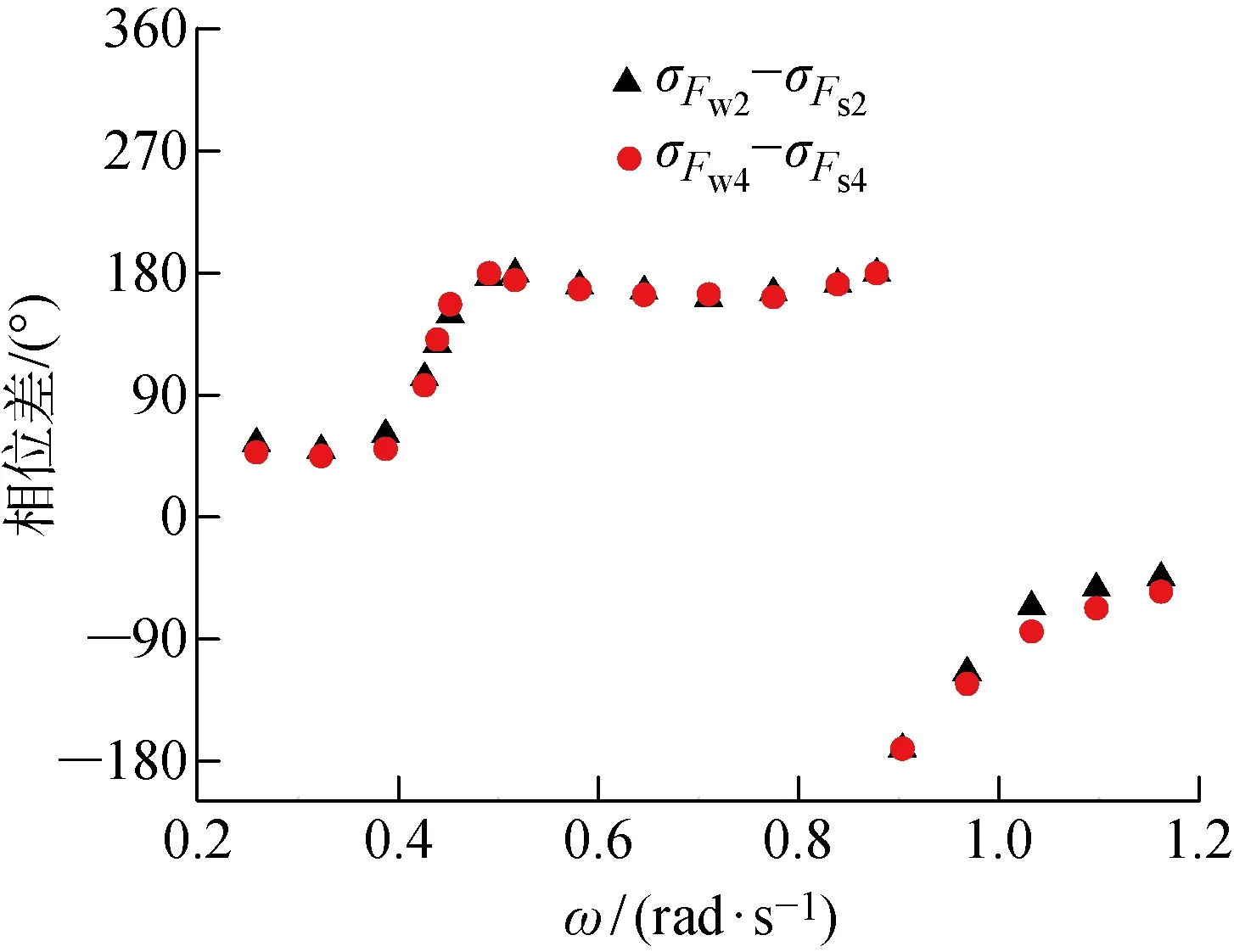
图10 横荡、横摇模态下波浪载荷与晃荡载荷相位差Fig.10 Phase shifts between wave load and sloshing load in sway and roll modes
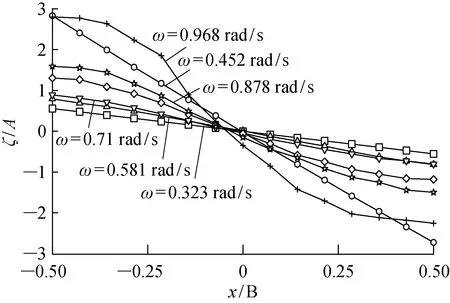
图11 不同激励频率下的波面形状Fig.11 Profiles of free surface under different frequencies
4 结果与讨论
4.1 船体运动与晃荡耦合机理
根据图8中的液体和固体装载下的船体运动响应RAO可以看出:船体的横荡、横摇运动受舱内晃荡影响显著,垂荡运动受晃荡影响较小.液舱装载时,船体的横荡运动随着波浪频率的增加逐渐减小,并在晃荡一阶固有频率处(ωs=0.886 rad/s)趋近于0;当波浪频率大于ωs时,横荡幅值出现新的响应峰值.船体横摇运动固有频率从固体装载时的 0.48 rad/s下降到液体装载时的 0.425 rad/s,这说明液舱晃荡减小了船体横摇模态下的回复力矩;同时晃荡也增加了船体受到的阻尼力,引起响应幅值的下降.图9给出了液舱内的晃荡自由面幅值ζ以及作用在船体横荡、横摇模态下的晃荡载荷Fs2和Fs4.可以看出,晃荡响应中出现了2个主要峰值,分别对应船体的横摇固有频率ωr,以及在大于ωs处的船体横荡运动峰值频率.图 10所示为横荡、横摇模态下波浪载荷与晃荡载荷相位差分布.可以看出,在低于横摇固有频率ωr和高于晃荡固有频域ωs的区间内相位差较小,也就是晃荡加大船体受到的载荷;而在ωr与ωs的频域区间内晃荡载荷与波浪载荷几乎相反(见图 8),船体运动响应随之减小.
图11所示为不同频率下沿壁面y=-W/2自由面最大幅值处的波面形状.可见,在低频区间内,波面形状更为平直(0.323,0.452,0.581 rad/s);在高频区间内,波面形状更为弯曲,为一阶模态振型(0.71,0.878,0.968 rad/s),同时呈现出一定的非线性特性(波谷较浅、波峰较高).这说明低频区间内船体横摇引起的液舱倾斜为舱内波面变化的主导激励.波面变化为准静态响应,波面幅值可以近似表示为(W/2)sinξ4,其中ξ4为船体横摇角度.此时静水压力在横摇模态上产生了很大载荷;但由于波面较为水平,横荡模态上的晃荡载荷很小.在高频区域尤其是晃荡固有频率ωs附近,船体的横荡运动为晃荡响应的主导激励,横荡模态上的晃荡载荷也急剧增加.在此频域附近晃荡与横摇运动耦合作用明显(见图8),横荡响应显著区别于固体载况.但由于ωs远离船体横摇运动固有模态,该频率附近的横摇运动响应增加较小.
4.2 液舱布置敏感性分析
液体装载船体的耦合响应对液舱的布置方式十分敏感.液舱的位置决定了晃荡载荷作用在船体上的位置.基于第2节中的液舱布置,通过调整液舱的位置以及布置方式研究晃荡作用对船体影响的变化趋势.
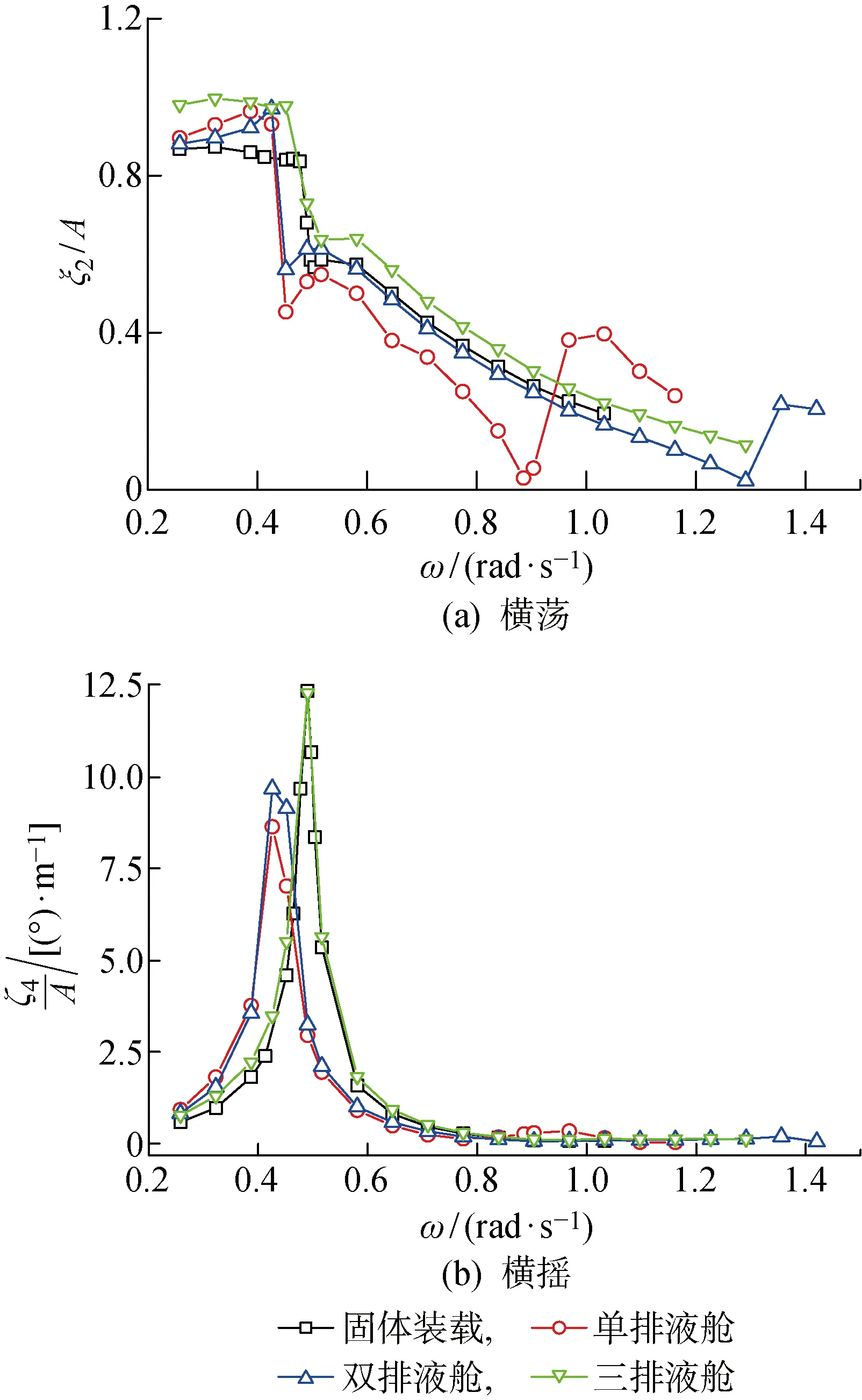
图12 横浪场景采用不同液舱布置方式时的船体运动响应RAOFig.12 RAOs of vessel’s motion with different tank arrangements under beam sea
4.2.1液舱划分影响 首先考虑液舱划分方式对耦合响应的影响.将液舱沿船宽方向等间距划分为双排和3排液舱布置.为保证船体总体惯量和液舱装载尺寸的一致,在划分中不考虑内部舱壁厚度,将液舱按照宽度进行均分.图12所示为横浪场景下采用固体装载、单排液舱、双排液舱和三排液舱布置时的船体运动响应RAO.图13所示为不同液舱布置方式对应的液舱晃荡响应.在双排和三排液舱布置场景下,液舱在宽度方向的ωs分别为 1.31 和 1.60 rad/s.
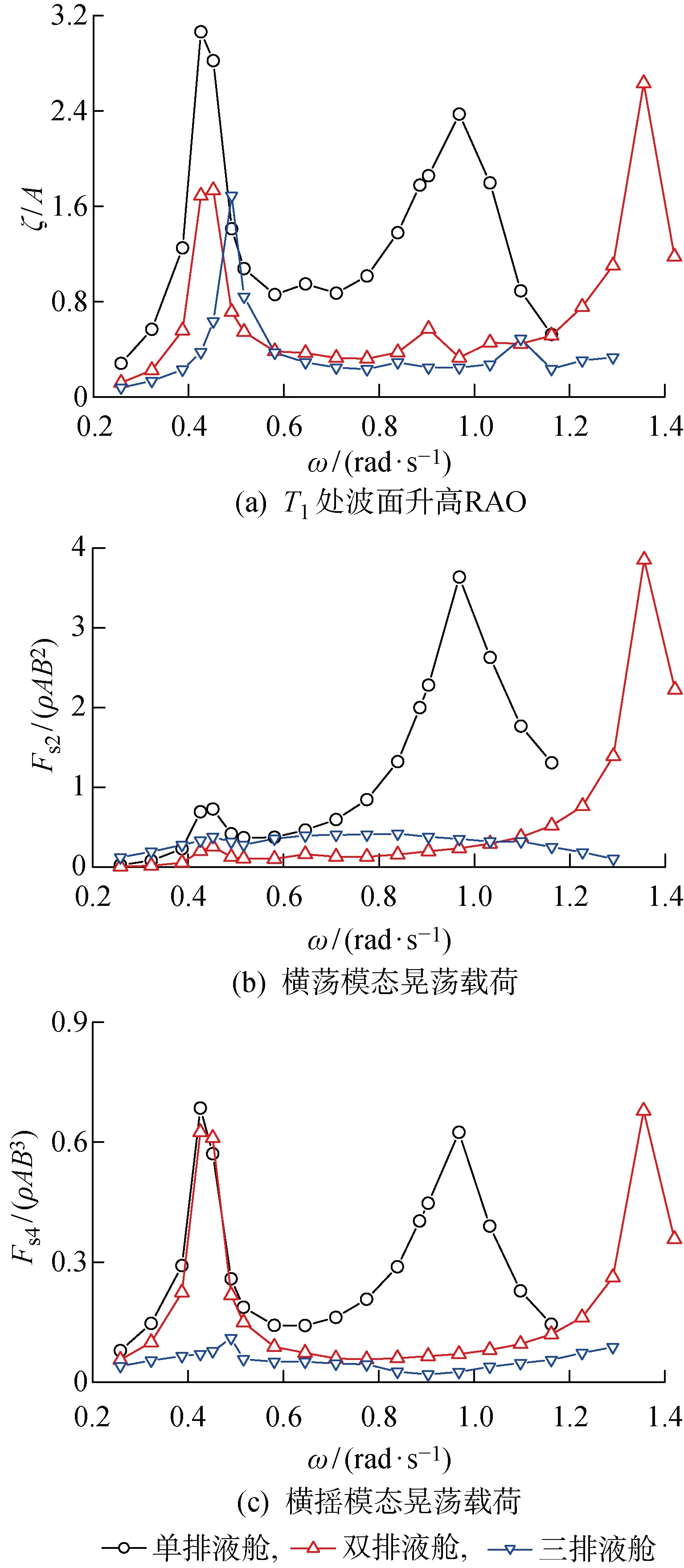
图13 横浪场景采用不同液舱布置方式时液舱晃荡的响应Fig.13 Sloshing responses in liquid tank with different arrangements under beam sea
由船体运动响应可以看出,随着液舱宽度减小,晃荡对船体横荡运动影响下降.这是由于液舱晃荡固有频率ωs远离了横荡运动的主要响应频率区间,但在ωs附近的晃荡响应依然很大,并引起了较大的横荡响应.由于液舱划分改变了液面的宽度,横摇模态下的耦合响应影响变化更为明显.由图13可以看出,双排布置时在横摇固有频率处的晃荡幅值下降近1/2.由4.1节中的分析可知,该频率下晃荡波面平整,晃荡幅值与液舱宽度呈线性关系.但晃荡产生的横摇力矩并没有明显变化,船体的横摇运动固有频率也未随着液舱宽度减半而发生显著变化,且横摇幅值有所增加.
在三排液舱布置场景下,ωs进一步远离船体横荡运动响应区间;同时更小的液面宽度减小了横摇引起的液舱晃荡.此时船体运动响应与固体装载时十分接近.由以上分析可知:采用多排液舱布置方式可显著减小晃荡对船体横摇运动的影响,对横荡运动的影响主要取决于晃荡固有频率与船体主要响应频率间的关系.
4.2.2液舱垂向位置影响 图4(a)中液舱底部到船底部距离dtank=4.8 m,将液舱分别上移和下移3 m后得到dtank=7.8 m和dtank=1.8 m的工况.船体总惯量参数不随液舱移动而变化.图14所示为液舱处于不同位置处船体在横浪作用下的运动响应RAO.可以看出,垂荡运动几乎不受液舱垂向位置变化的影响,横摇运动的频率和幅值均发生显著变化.由于横荡运动和横摇运动的耦合作用,横荡运动在横摇固有频率处的响应也相应变化,但在横摇运动影响较小的频率区间内横荡运动对液舱位置的变化不敏感.从图15中的晃荡响应可以看出,在横荡激励为主导的高频区域内,晃荡幅值与横荡方向上的晃荡载荷受液舱垂向位置影响很小.
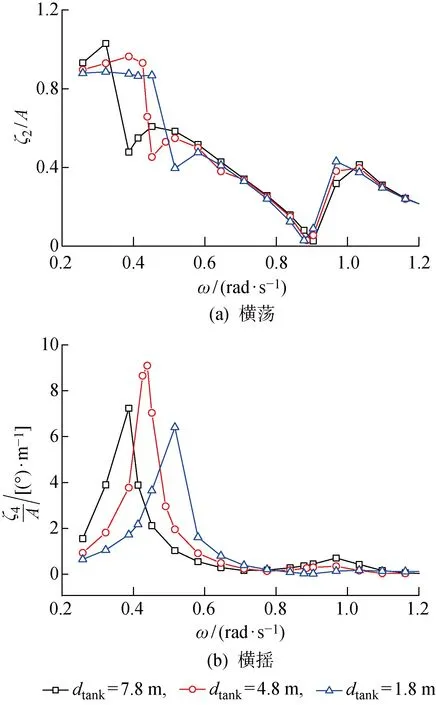
图14 横浪场景下液舱在不同位置处的船体运动响应RAOFig.14 RAOs of vessel’s motion with different locations of liquid tank under beam sea
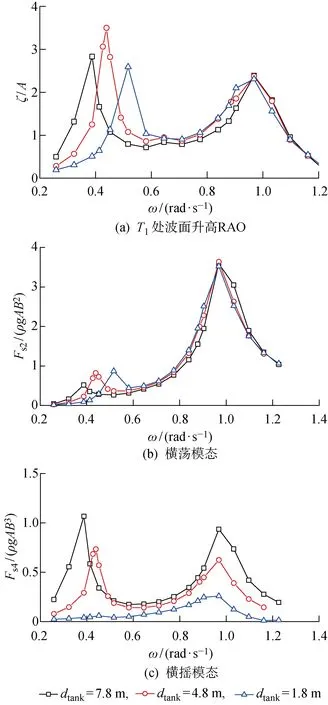
图15 横浪场景下液舱在不同位置处的晃荡响应Fig.15 Sloshing responses in liquid tank with different locations under beam sea
从横摇运动RAO可以看出:随着液舱位置的提升,船体的横摇固有频率进一步下降;而随着液舱位置的下降,船体横摇固有频率有所增加.从图15中的晃荡力矩可知,随着液舱位置提升,晃荡载荷显著增加.这一方面是由于液舱到船体旋转中心距离增加,舱壁受到的旋转激励增加;另一方面,较高的液舱位置增加了晃荡载荷的力矩,使得晃荡载荷对船体的作用更为强烈.由 3.2 节的分析可知,横摇固有频率远小于晃荡固有频率ωs,晃荡的动态响应不剧烈.因此可知静水横摇载荷的变化为晃荡影响变化的主要原因.
5 结论
本文基于势流理论在时域内对液体装载船体的耦合响应进行数值预报,并开展相关的模型试验对数值模拟程序进行验证.基于数值计算和试验结果,对液舱晃荡和船体运动间的耦合机理进行了研究,同时分析了液舱布置方式对耦合响应的影响.得到的主要结论如下:
(1)横浪场景下晃荡与船体的横荡、横摇运动耦合显著,与垂荡运动耦合较弱.晃荡主要响应峰值频率处于横摇固有频率和晃荡一阶固有频率附近,分别主要由横摇和横荡激励引起.船体运动响应主要受晃荡载荷与波浪载荷间的相位差影响.
(2)采用多排液舱布置可以减小液面宽度,进而减小晃荡载荷对横摇运动的敏感程度;而晃荡对横荡运动的影响特性不变,耦合响应结果主要由晃荡固有频率决定.
(3)液舱垂向位置的变化对横摇模态的耦合响应影响明显.当液舱位置较高时晃荡载荷对船体的横摇运动影响更大.船体横荡、垂荡运动对液舱垂向位置变化不敏感.

