基于传感探测系统的多自治水下机器人编队协调控制
庞师坤,王 健,易 宏,梁晓锋
(上海交通大学 海洋智能装备与系统教育部重点实验室;海洋工程国家重点实验室,上海 200240)
自治水下机器人(AUV)以其独特的优势在海底侦查、探索等领域发挥着极其重要的作用.对于一些复杂任务,如大范围协同侦查、对抗、打击和水下信息组网[1]等,AUV协同编队可以协作完成,而单个AUV却由于自身的局限性而难以胜任.因此,越来越多的学者将研究重点聚焦于AUV协同编队控制.编队控制是指多个机器人在达到目的地的过程中保持某种队形,同时又要适应环境约束的控制技术[2].目前,编队控制方法主要有基于行为法[3-4]、人工势场法[5]、虚拟结构法[6]、领航-跟随法[7-13]、分布式控制法[14]等.
领航-跟随法由于其可行性高、扩展性强等特点,被众多学者广泛采用.Shojaei[7]基于视觉法利用领航-跟随法的基本思想对AUV目标追踪进行了深入研究,同时对水面欠驱动无人艇编队控制进行了分析;Rout等[8]研究了在领航AUV和跟随AUV之间存在间断性信息传输条件下的编队协调控制;Das等[9]对AUV编队进行了综述性介绍,并在文献[10]中对通信限制条件下的AUV领航-跟随编队进行了研究;丁国华等[11]对多AUV主从式编队及其避障控制方法进行了研究,提出了一种基于反步控制法和人工势场法的多AUV三维编队与避障方法;朱大奇等[2]研究了基于领航位置信息的AUV三维编队控制方法;向先波[12]研究了二阶非完整性水下机器人路径跟踪控制,对基于路径跟踪的AUV编队协调控制进行了研究,并在后续工作中[13]以海底光(电)缆为编队探测目标,对AUV编队在平面和三维空间内协调控制进行了探索.
由以上分析可以看出,在编队中AUV个体之间经常需要依靠水声通信传递信息,然而该通信方式容易造成信息延迟、数据丢失等问题.如果采取传感器探测的方式进行编队,那么跟随AUV能够实时探测领航AUV的相对位姿信息等,编队个体之间不存在信息交互,这种非通信式编队可以有效避免上述问题.在传感器探测条件下,本文采用领航-跟随法对AUV编队进行研究,同时利用Lyapunov函数设计了反演控制器,提高了编队系统的稳定性和可靠性.
1 问题描述
1.1 AUV运动学和动力学模型
假设AUV是左右对称的,并且惯性矩阵、附加质量矩阵、水动力阻尼矩阵均是对角矩阵,忽略其垂荡、横滚和俯仰运动,在无外界干扰时的运动学和动力学方程为[6]
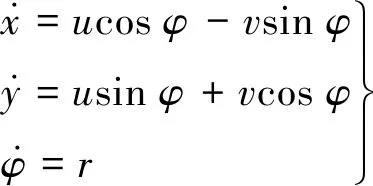
(1)
(2)
式中:(x,y)为AUV在大地坐标系下的位置;φ为大地坐标系下的艏向角;u、v和r分别为随体坐标系下的纵向速度、横向速度和艏向角转动的角速度;mi(i=1,2,3)为包含附加质量在内的惯性质量;di(i=1,2,3)为横向、纵向和艏向的水动力系数;τu和τr分别为纵向力和偏航力矩的控制信号.
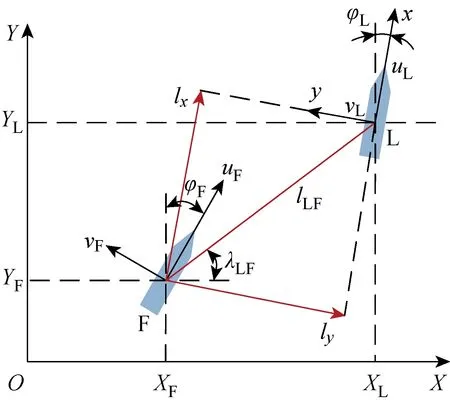
图1 领航-跟随编队构型Fig.1 Leader-follower formation structure
1.2 领航-跟随编队控制
本文中领航AUV用L表示,跟随AUV用F表示.在笛卡尔坐标系内,领航AUV与跟随AUV的编队几何构型如图1所示.图中:(XL,YL,φL)为领航AUV的位置和艏向角;(XF,YF,φF)为跟随AUV的位置和艏向角;(lLF,λLF)为领航者和跟随者之间的相对位置和视线角度;lx和ly分别为跟随AUV相对于领航AUV在x和y方向上的投影.编队定义为
FLF=[lLFλLF]T
(3)
lLF∈R>0,λLF∈[0,π]
理想AUV编队定义为
(4)
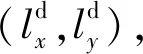
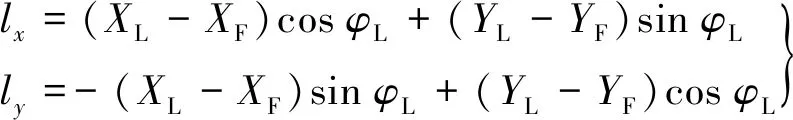
(5)
(6)
综合式(1)~(5),可以得到AUV编队的运动学模型:
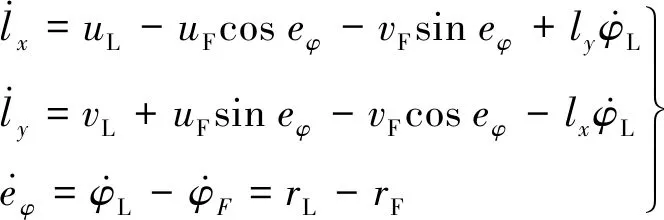
(7)
x和y方向上的位置误差为
(8)
联立式(6)~(8),得到编队系统的误差模型:
(9)
因此,控制任务是为跟随AUV设计控制器,使得系统误差趋近于零,得到理想的编队状态,即
(10)
Δ∈(-π/2,π/2)
式中:当Δ=0时,编队控制中跟随AUV的艏向始终与领航AUV保持一致.
1.3 视觉传感器分析
本文编队中AUV均装备了前向传感探测系统,每个传感探测系统都假设有传感探测限制.图2中所示扇形的半径Drange和角度2α定义了传感探测区域.因此,每个AUV可以测量到在传感探测区域内的物体.当且仅当跟随AUV能够探测到领航AUV时,图2中的2艘AUV可以组成编队队形.
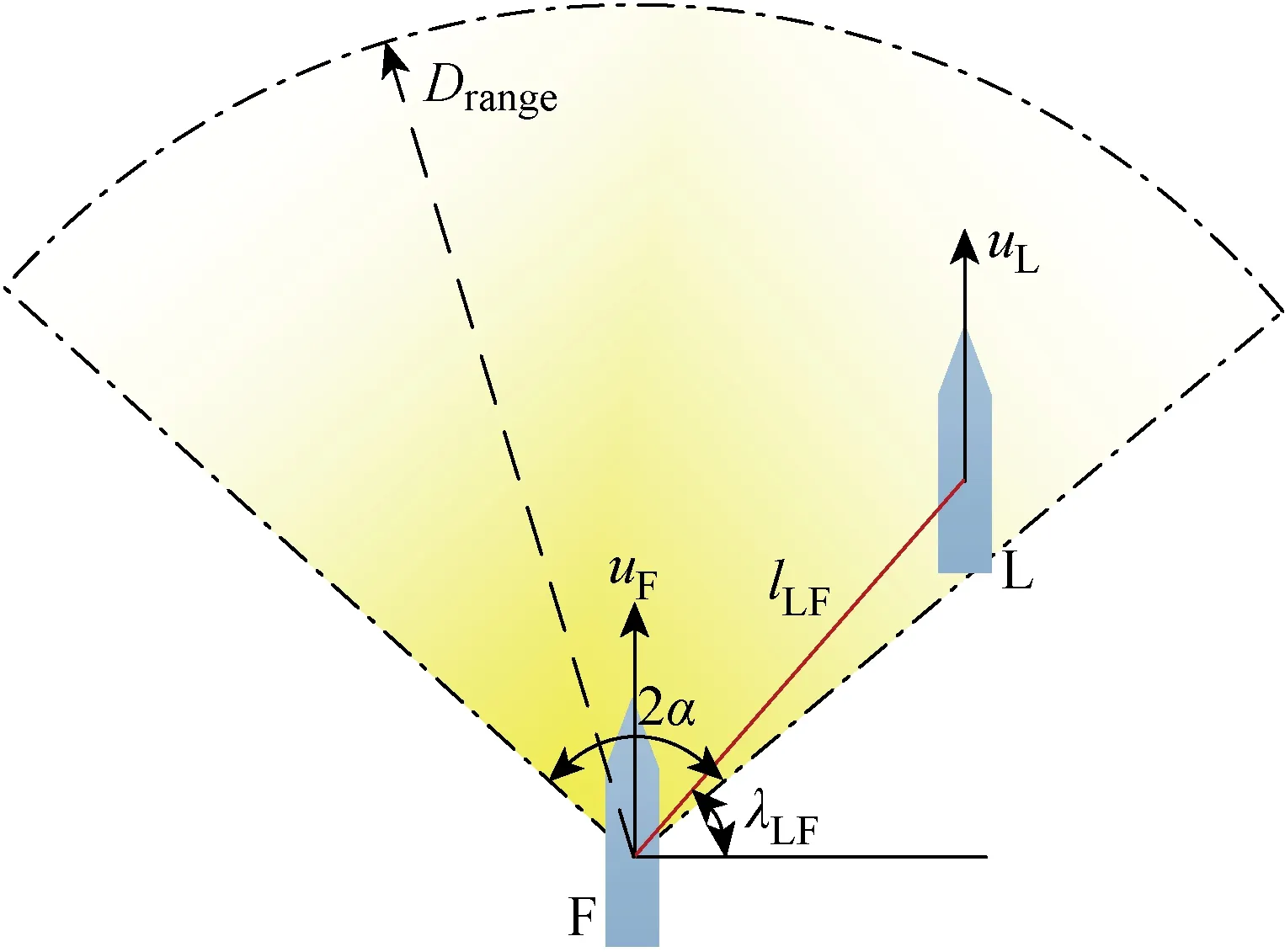
图2 传感探测区域Fig.2 Sensor measuring region
为方便模拟,本文做如下假设:
(1)编队状态向量和领航AUV的方向能够被传感探测传感器准确地探测到,速度则根据探测到的时间导数进行计算.
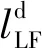
(3)每艘AUV的速度和方向只有自己可知,互相之间没有干扰和阻碍.
2 编队控制器设计
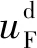
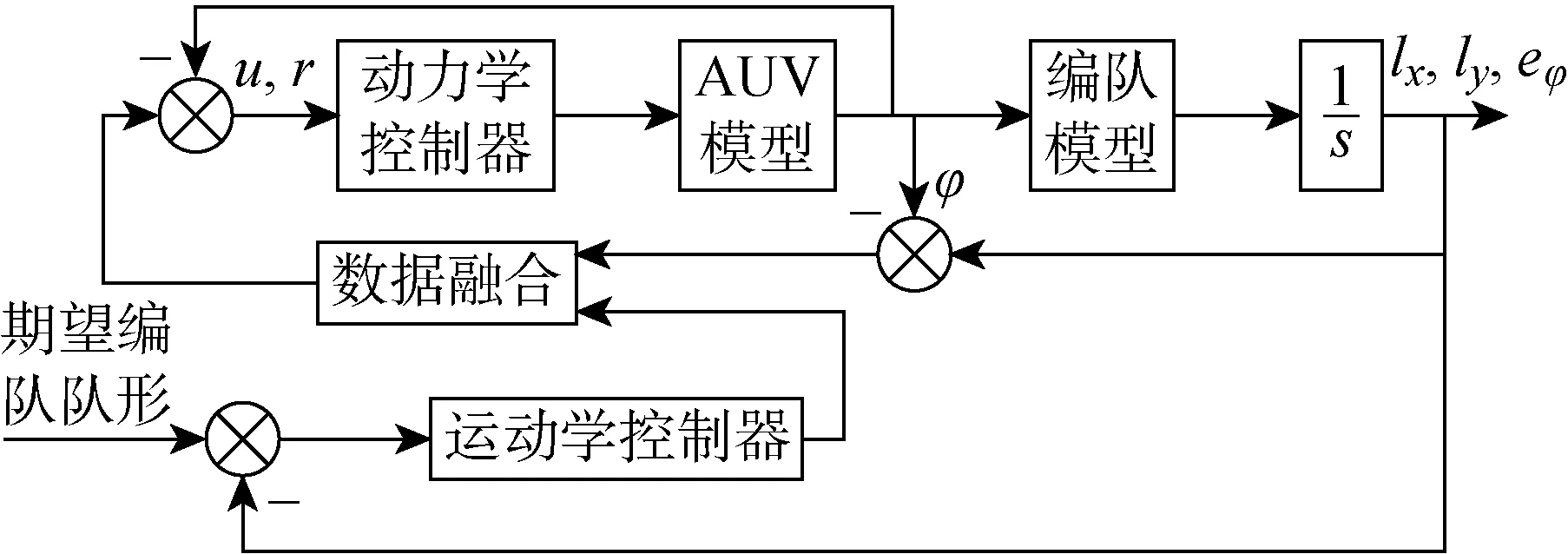
图3 跟随AUV控制策略Fig.3 Control strategy of follower AUVs
2.1 运动学控制器
首先定义转换矩阵
(11)
然后将式(8)中的距离误差到跟随AUV的随体坐标系下:
Σ=ReφE
(12)
式中:Σ=[ε1ε2]T;E=[exey]T.由此可得
(13)
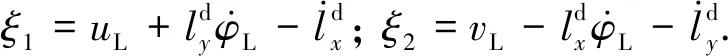
确定Lyapunov控制函数(CLF):
ε1(uF-ξ1coseφ+ξ2sineφ)+
ε2(vF-ξ1sineφ-ξ2coseφ)
(14)
运动学控制律为
(15)
(16)
式中:k1,k2>0;k1,k2∈R.
式(14)可以写成
(17)
由此可见,系统是渐近稳定的.
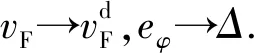
定义纵向速度误差
(18)
联立式(15)和(16),可得
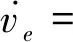
k2(vF-ξ1sineφ-ξ2coseφ-ε1rF)-
(19)
另外,k1=d1/m1,k2=d2/m2,式(19)可以表示为
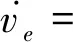
(ξ2sineφ-ξ1coseφ)rL-
(20)
定义CLF:
(21)
从而得到
(22)
式中:λ=ξ2sineφ-ξ1coseφ;ζ=ξ1sineφ+ξ2coseφ.
选择虚拟控制律为
(23)
式中:
式(22)变为
(24)
式中:σ为任意有界无穷小常数.
由此可见,系统(ve,eφ)是渐近稳定的.
2.2 动力学控制器
(1)定义纵向速度误差
(25)
其时间导数为
(26)
定义CLF:
(27)
联立式(27)和(2),可得
(28)
控制律为
(29)
k6>0,k6∈R
式(28)变为
(30)
(2)定义角速度误差
(31)
其时间导数为
(32)
定义CLF:
(33)
联立式(33)和(2),可得
(34)
控制律为
(35)
k7>0,k7∈R
则式(34)可表示为
(36)
由此可见,系统是渐进稳定的.
3 仿真分析
在仿真分析中,设定AUV传感探测系统的探测范围是2α∈[0,π],由3艘具有相同参数的AUV组成编队[15],其中,1艘作为领航者,另外2艘作为跟随者.领航AUV根据设定的轨迹航行,跟随AUV则按照编队控制器产生的轨迹航行,从而得到期望的编队队形.AUV参数:m1=1 116 kg,m2=2 133 kg,m3=2 133 kg,d1=25.5 kg/s,d2=138 kg/s,d3=138 kg/s.
算例1期望的控制模型参数:lLF1=5 m,λLF1=π/4,lLF2=5 m,λLF2=3π/4.初始位置分别为:领航AUV,[XL,YL]=[0,0];跟随AUV1,[XF1,YF1]=[0,-5] m;跟随AUV2,[XF2,YF2]=[0,5] m.
领航AUV和跟随AUV的初始速度分别为:uL=1 m/s,vL=0 m/s,rL=0.01 rad/s,速度和转艏角速度保持不变;跟随AUV1,[uF1,vF1,rF1]=[0,0,0];跟随AUV2,[uF2,vF2,rF2]=[0,0,0].
仿真结果如图4~6所示.从图4中可以看出领航AUV做匀速圆周运动且初始状态时与跟随AUV处于非编队队形,控制器会控制跟随AUV调整相应的运动轨迹,从而得到期望的编队队形.由图5和6可知,在X和Y方向,2个跟随AUV的位置误差很快趋近于零;由于做圆周运动,领航AUV的艏向在均匀变化,在达到稳定状态后跟随AUV的艏向则与其保持固定的误差,大约在2° 左右.
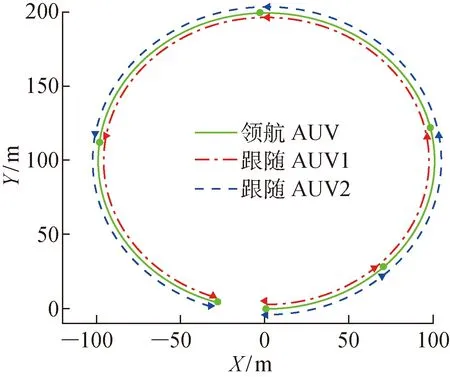
图4 圆周运动时AUV编队轨迹Fig.4 AUV trajectory of circling motion
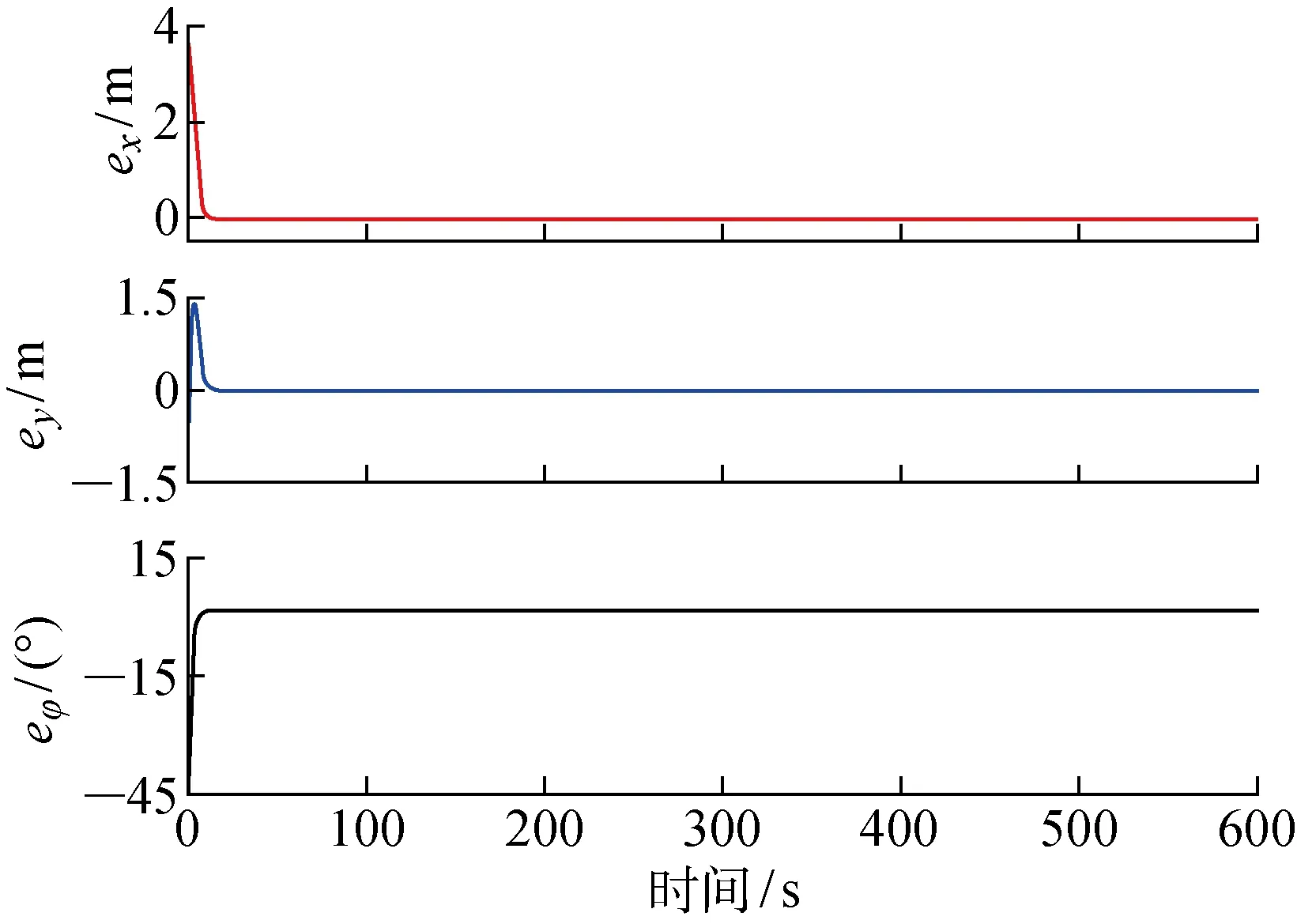
图5 圆周运动时跟随AUV1误差Fig.5 Errors of follower AUV1 of circling motion
图6 圆周运动时跟随AUV2误差Fig.6 Errors of follower AUV2 of circling motion
算例2期望的控制模型参数:lLF1=3 m,λLF1=π/3,lLF2=6 m,λLF2=2π/3.初始位置分别为:领航AUV,[XL,YL]=[0,0];跟随AUV1,[XF1,YF1]=[-6,-6] m;跟随AUV2,[XF2,YF2]=[-6,6] m.
领航AUV初始速度:uL=1 m/s,vL=0 m/s,rL=0 rad/s,速度始终保持不变;跟随AUV1,[uF1,vF1,rF1]=[0,0,0];跟随AUV2,[uF2,vF2,rF2]=[0,0,0].
仿真结果如图7~9所示.由图7可知,当领航AUV做匀速直线运动、2个跟随AUV与领航AUV的距离不同且初始位置处于领航AUV异侧时,同样可以按照设定的编队条件得到期望的编队队形.由图8和9可以看出,虽然在初始的队形形成阶段,跟随AUV位置和艏向均有较大变化,但2个跟随AUV的位置误差和艏向误差均在较短时间内收敛于0,并最终完成编队,与理论值相符.
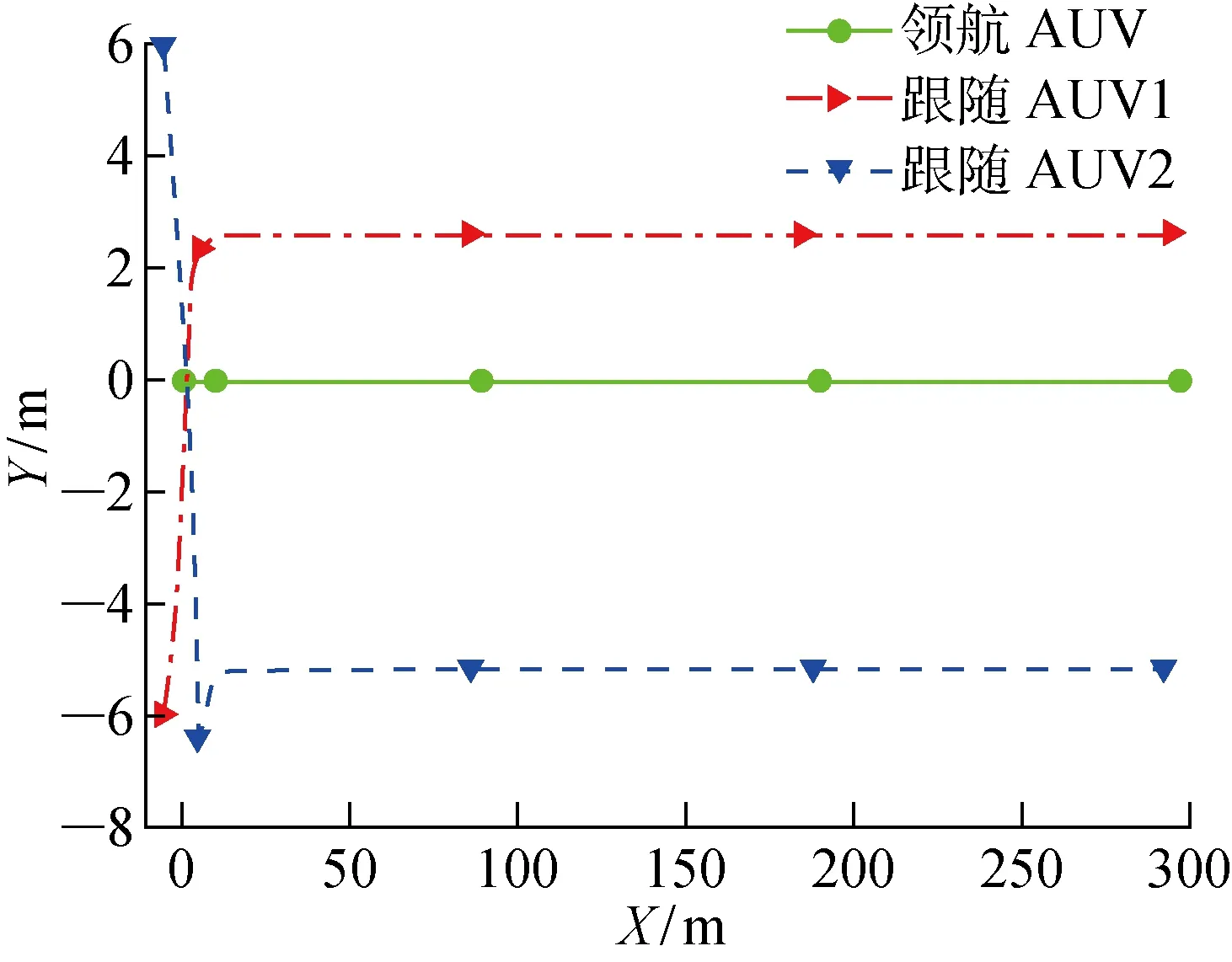
图7 直线运动时AUV编队轨迹Fig.7 AUV trajectory of rectilinear motion
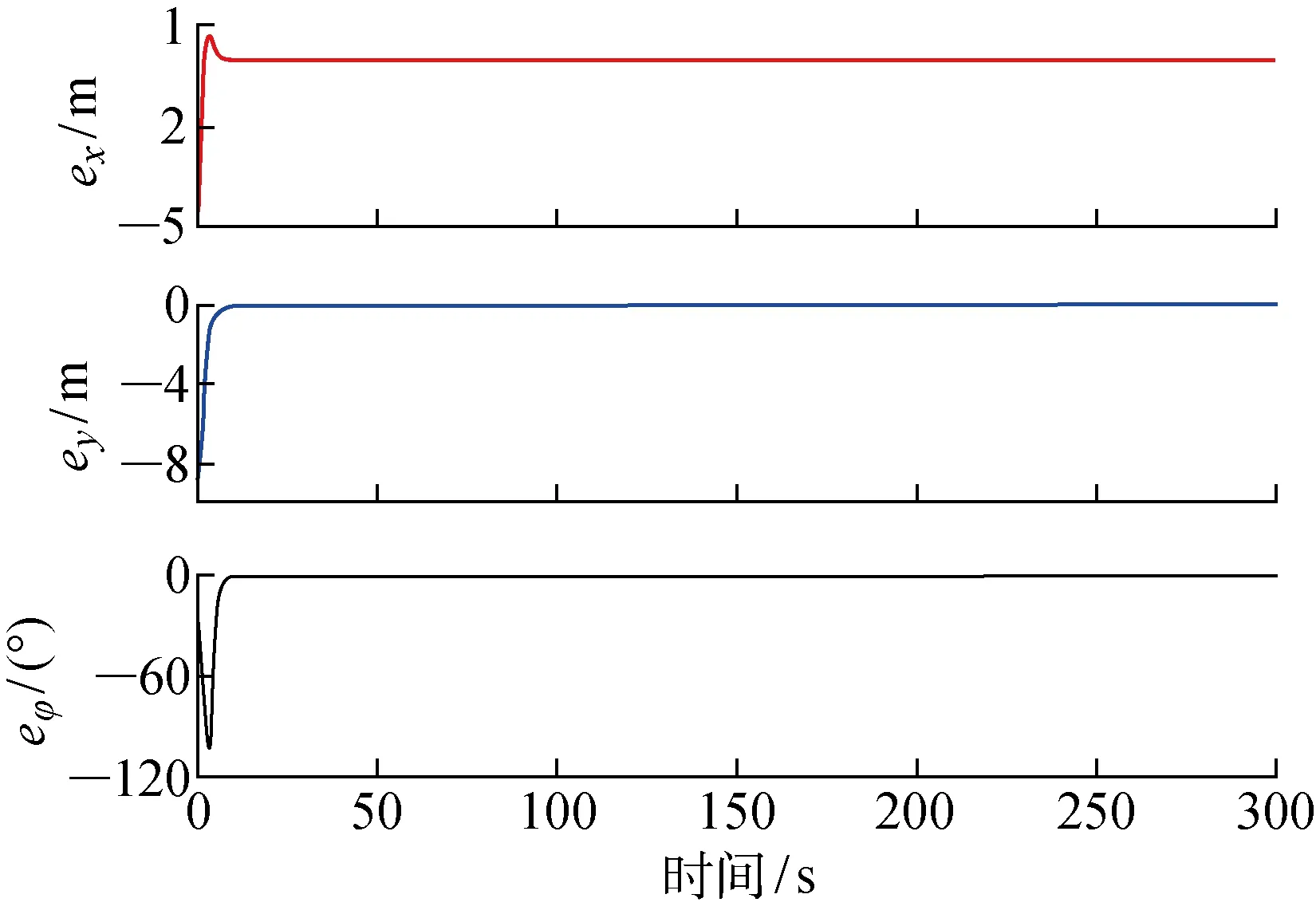
图8 直线运动时跟随AUV1误差Fig.8 Errors of follower AUV1 of rectilinear motion
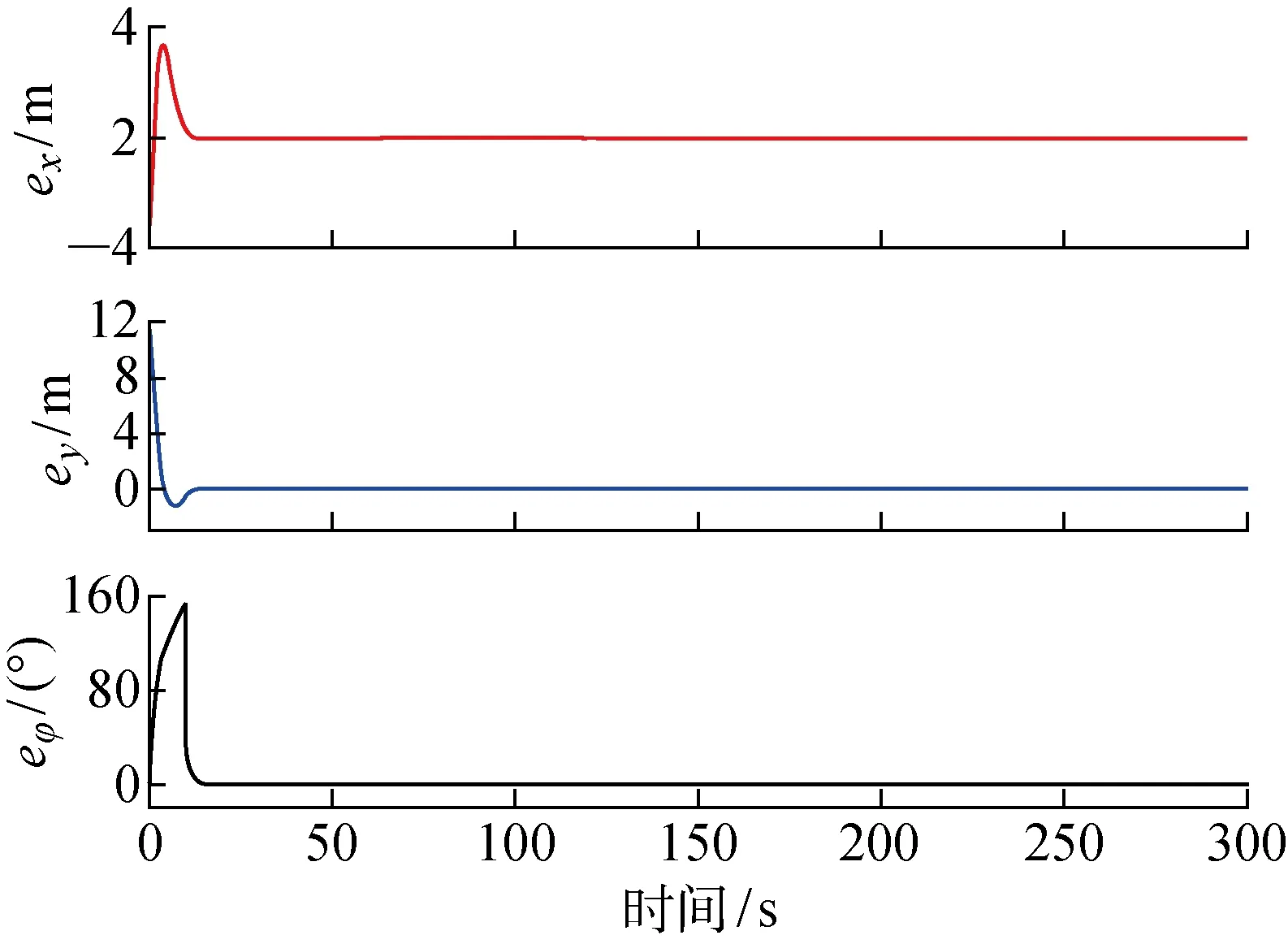
图9 直线运动时跟随AUV2 误差Fig.9 Errors of follower AUV2 of rectilinear motion
4 结语
编队中AUV之间依靠水声通信容易造成数据丢失和通信延迟等问题,而基于传感器探测的编队方式,AUV个体之间不需要通信,因此可以避免上述问题.本文在传感器探测条件下,采用领航-跟随法对AUV编队进行了研究.同时,利用Lyapunov函数设计了编队控制器,并证明了系统稳定性.随后将该控制器应用到具体AUV模型上,对领航AUV做圆周运动和直线运动轨迹进行仿真计算.结果表明,跟随AUV能够与领航AUV保持期望的位姿关系,得到期望的编队队形,验证了方法的有效性和实用性.本文所设计的控制器比较适用于近距离摄像和声纳探测系统,对于较远距离声纳探测,根据实际工作环境则需要考虑外部扰动及通信延迟等因素影响,作者将继续对此进行研究.

