基于光滑粒子流体动力学方法与TANH本构方程的钛合金切屑形态预测

牛伟龙，莫 蓉，孙惠斌，韩周鹏

(西北工业大学 现代设计与集成制造技术教育部重点实验室，西安 710072)

钛合金Ti-6Al-4V具有低密度、高强度、抗腐蚀性等优点，常被用作航空航天等领域的加工材料，而这种具有高硬度、低热物理性能的材料在切削加工时往往容易产生锯齿形切屑[1].由于锯齿形切屑在形成过程中容易引起机床的振动，影响工件表面的加工质量，减少刀具寿命，所以对钛合金锯齿形切屑的形成机理研究有着重要的意义.但钛合金是一种难加工材料，且价格昂贵，以实验的方法研究它的形成机理费时费力，且成本较高.近年来，随着计算机技术不断的发展，计算机模拟切削过程成为了研究它的一种重要手段.

然而，大部分学者建立钛合金切削模型时都是基于有限元方法(FEM)，且模型往往都将重点放在切削力预测上，对切屑形态的预测不够准确，甚至无法模拟出锯齿形切屑，这也从侧面反映出钛合金切削数值模型的精度不高.近年来，随着对钛合金加工精度要求的不断提高，钛合金锯齿形切屑对工件的影响也逐渐被研究者重视起来，一些学者也开始对其形成过程进行分析和模拟.Su等[2]基于塑性金属材料塑脆性转化，研究了高速切削锯齿形切屑形成过程和机理，并揭示了锯齿形切屑形成时切屑分节的变化规律和集中剪切带的启动与扩展路径；Zhang等[3]提出了一种基于本征自洽法的流动应力模型，将钛合金的化学成分和α相、β相晶体结构对材料的流动应力的影响都考虑在内，模拟出了钛合金在高速切削下的锯齿形切屑；Chen 等[4]采用Jonhson-Cook(JC)模型以及能量的塑性失效准则模拟钛合金锯齿形切屑的形成.但目前现有的大部分切削模型对切屑形态的预测往往精度不高，其原因主要有以下几点：① 大部分切削模型都是基于FEM所建立，其最大缺点就是依赖网格，当模拟大变形问题时(锯齿形切屑的形成)容易发生网格畸变，从而造成计算精度不高；② 网格的划分方式没有统一的标准，为模拟锯齿形切屑的形成，建模者往往跟据经验进行网格划分，造成不同建模者所建立的模型结果差别很大；③ 切屑与工件的分离需要设置分离层和分离准则，在切屑与工件分离时需要删除分离层，无法实现切屑与工件的自然分离；④ 大部分模型采用JC本构模型或JC损伤本构模型，而这两种本构模型无法描述在大应变状态下的材料动态力学性能.

为解决以上缺点，研究采用一种无网格方法——光滑粒子流体动力学(SPH)方法对钛合金切削过程进行模拟.由于该方法是一种拉格朗日形式的无网格粒子法，相对于传统的基于网格的FEM，它的自适应性在场变量早期便得到了，同时它的公式构造并不受粒子分布的影响，所以可以很自然处理一些具有大变形的问题[5]，如切屑分离和锯齿形切屑的形成.

同时，研究还引入了一种名为TANH的材料本构模型，相对于JC模型和JC损伤模型，它可以准确描述出钛合金在大应变下材料流动应力与应变的关系.由于在切削过程中，钛合金受到刀具的挤压，内部晶体结构发生破坏，产生新的晶体结构后，材料在发生形变过程中的流动应力最终会趋于稳定.TANH模型也将这一过程考虑在内，全面描述了切削过程中钛合金材料的动态力学性能.

综上所述，基于SPH方法，结合TANH本构模型，以Fortran90为模型开发平台，通过分析TANH模型中的修正参数对材料应力应变曲线变化的影响，标定出TANH模型中最优修正参数，使整个切削模型相较于传统的切屑模型更加准确和可靠.最后通过实验验证了模型的准确性.

1 SPH基本原理

SPH方法在1977年被Lucy首次提出[6]，它最先被用于天体物理现象的模拟，随后被广泛应用于连续固体力学[7-9]和流体力学[10-12]中.SPH方法与FEM不同，它是一种拉格朗日形式的无网格粒子方法，其核心思想如下：

(1)由任意分布的粒子来表示问题域，粒子之间不需要任何连接.

(2)近似的场函数由积分法来表示.

(3)将核近似方程应用粒子来进一步近似.

(4)所应用的粒子取决于当前局部分布的粒子(局部粒子的多少由光滑长度决定)，粒子的近似过程在每一个时间步内都要进行.

(5)速度、能量、密度等场变量的偏微分方程都会用到粒子近似法，从而得到一系列与时间相关的离散化常微分方程.

(6)通过显示积分法求解常微分方程，得到以时间为变量的所有粒子的场变量值.

SPH方法的关键步骤有两步：

(1)核函数近似

(1)

式中：Ω为该点粒子的支持域；xi和xj为粒子i与粒子j相应位置的函数变量；W为光滑核函数，h为光滑长度，用来定义光滑核函数影响区域的范围.根据文献[13]选取三次样条光滑函数作为研究SPH的核函数：

(2)

式中：αd=15/(7πh2)为归一化因子；q=rij/h,rij是粒子i和粒子j之间的距离，h的大小取决于实际问题，过大可能影响计算效率，过小会造成精度不高.在本研究中，采用 1.5 倍的粒子间距(该间距在初始设置时给出)作为光滑长度.

(2)粒子近似.在SPH方法中，可以使用粒子的体积ΔVj来取代式(1)中粒子j处的无穷小单元dxj，因此，粒子j的体积可以表示为

ΔVj=mj/ρj

(3)

式中：mj为粒子j的质量(j=1,2,…,N)，N为粒子j支持域内的所有粒子总数；ρj为粒子的密度.将式(3)代入式(1)可得粒子i处的近似式为

(4)

综上，可以看出SPH方法的实质就是将一些宏观变量(温度、压力、密度等)通过一组无序点的值表示成积分的形式.在这组点中，各个点之间的相互作用通过插值函数来描述，并利用插值函数给出各点处的核函数的近似估计值.

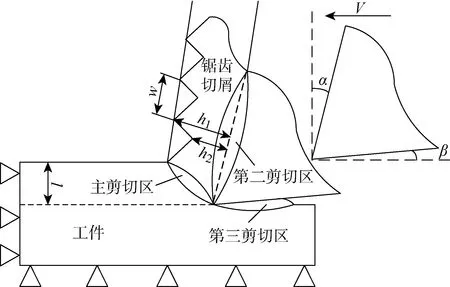
图1 切削模型Fig.1 Cutting model

2 数值模型的建立

2.1 SPH切削模型

研究将刀具看成刚体，建立二维的SPH切削模型.如图1所示，切削参数有切削速度V、切削前角α、切削后角β、切屑齿高(h1、h2)、齿距w和切削深度l.模型基于Fortran90平台开发，程序基本结构如图2所示.图3所示为一个工件的切削模型，工件尺寸在模型中定义为1 mm×2 mm，由 20 000 个粒子组成，每一个粒子都携带着工件的材料属性，如质量、密度等.由于各个粒子之间不存在拓扑关系，所以模型可以在刀具切削过程中实现切屑和工件的自然分离，不存在FEM中网格发生畸变等问题.

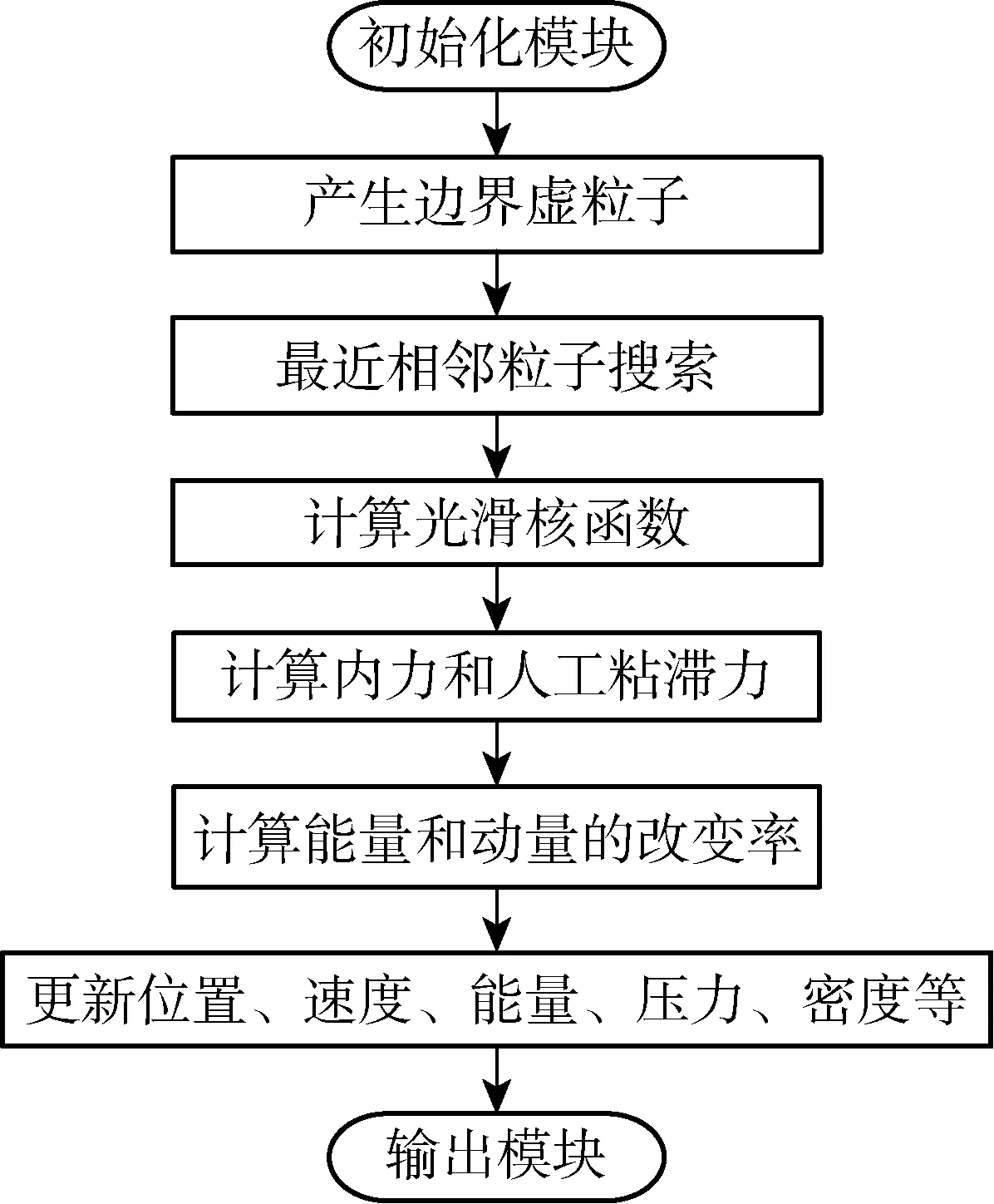
图2 SPH程序结构Fig.2 SPH program structure

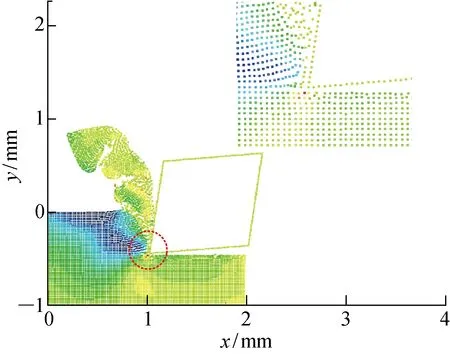
图3 SPH切削模型Fig.3 SPH Cutting model

2.2 TANH本构模型

对于切削模型，它的求解能力及精度除了与材料本身的物理性能相关外，还与材料的动态力学性能相关.而材料的本构方程就是用来描述材料的动态力学性能，它不仅是研究金属变形的重要基础，更是模拟切削加工过程的关键.

JC模型[14]是目前应用最为广泛的金属材料本构模型，它综合考虑了温度、应变与应变率之间的关系，形式简单，物理意义清楚.对于材料在变形过程中所发生的应变和应变率强化以及热软化现象都可以描述，但JC模型无法描述钛合金在大应变情况下的应变软化现象，也无法模拟钛合金形成的锯齿形切屑.为此，许多学者在JC模型的基础上加入损伤模型[15]，虽然加入JC损伤模型可以模拟出切削过程中钛合金Ti-6Al-4V锯齿形切屑的形成，但JC损伤模型所描述的应力与应变关系与材料的实际变化过程并不完全相符.图4所示为材料在整个变形阶段的应力应变曲线图，实线描述材料在发生变形时的实际应力与应变关系，而虚线为JC模型和JC损伤模型描述材料的应力与应变关系.由此可见，在材料发生小应变的情况下,JC和JC损伤模型都可以准确描述出材料的动态力学性能，但随着材料应变的增大，两个模型都无法作出准确的描述.

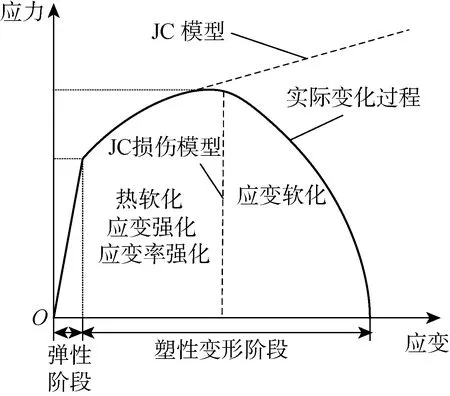
图4 不同本构模型的应力与应变变化规律Fig.4 Stress-strain curve of different constitutive models

TANH模型[16-18]是在JC模型的基础上建立的，由于JC模型只考虑材料的应变强化、应变率强化以及热软化，没有考虑材料在大应变下的应变软化现象，而JC损伤模型虽然可以模拟出锯齿形切屑，但是它是通过将材料在大应变下的流动应力设置为0而模拟出的，不符合材料流动应力的实际变化规律.TANH模型不仅考虑了材料的应力软化现象，也考虑了材料的再结晶现象，即材料的流动应力σ随应变ε的增大最终会趋于稳定.其表达式为

(7)

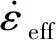
图6所示为材料在应变率为 2 000 s-1下JC和TANH模型的应力(σ)应变(ε)曲线图，从图中可以看出：应变小于 0.3 时，TANH模型与JC模型曲线基本拟合；当应变大于 0.3 后，JC模型的应力随应变的增加一直增大，TANH模型的应力开始减小，并随后趋于稳定.TANH模型这种变化趋势符合钛合金在大应变下发生的应变软化现象.这里值得注意的是随着应变的增加，TANH模型描述的应力最终不为0，而是稳定在某一值，这是由于钛合金材料受到外力破坏，材料晶体结构发生了破坏再结晶的现象，这也证明了TANH模型能准确描述钛合金在形变过程中的动态力学性能.

表1 材料和TANH模型参数[19-20]Tab.1 Parameters of material and TANH model[19-20]

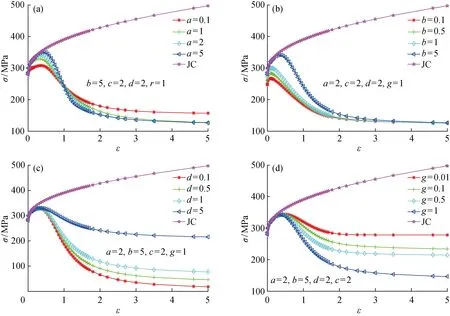
图5 参数对应力应变曲线的影响Fig.5 Influence of parameters on the stress-strain curves

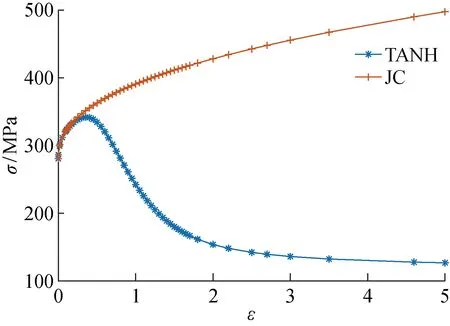
图6 JC和TANH模型的应力应变曲线Fig.6 Stress-strain curves of JC and TANH model

2.3 接触算法

如图7(a)所示，刀具由粒子构成，由于刀具是刚体，刀具粒子不携带材料的任何属性，并且由于是高速切削，发生的是绝热剪切，故也无需考虑刀具的导热性.温度则由SPH中温度计算公式进行计算[5]，这里只需赋予刀具粒子的位置信息和速度信息，而这些信息则由刀具的初始位置以及刀具的速度来确定.在获得这些信息后，利用这些表面粒子的位置信息和速度信息来计算表面粒子的法向量和切向量，通过这些向量来决定切削力的方向以及判断刀具表面粒子和工件表面粒子接触位置.当刀具表面粒子接近工件的粒子时，两种不同类型的产生相互作用力.

计算接触力有两个步骤，首先需要判断两粒子是否接触，在这里设置接触阈值，即当两种不同类型的粒子间距小于或等于某一值时，两种粒子被判断为发生接触，它们之间发生相互作用，产生相互作用力.这里值得注意的是，刀尖圆弧半径R与刀尖粒子的接触阈值相等，即这里可以将R设置为刀尖粒子的接触阈值.如图7(b)所示，点p为工件粒子i到刀具表面的垂点，dp为工件粒子i到刀具表面粒子的实际垂直距离，d0为两种粒子的接触阈值.当dp≤d0时，接触发生.p点处的切向量τp和法向量np的计算式为

(8)

式中：Xk+1=(xk+1,yk+1)和Xk=(xk,yk)为刀具表面粒子k+1和粒子k的坐标值.

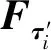
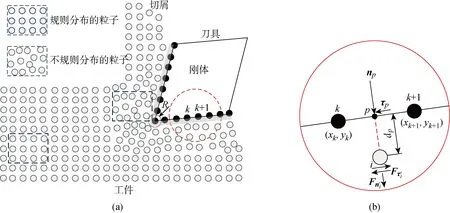
图7 SPH切削模型和粒子之间交互作用Fig.7 SPH cutting model and the particles interaction

(9)

式中：mi为粒子i的质量；vpi=vp-vi，vp为点p处的速度，即刀具速度，vi为粒子i的速度；μ为刀具与工件之间的摩擦系数；Δt为时间增量.利用上式可计算刀具和工件的受力情况[13-16].

3 实例验证及讨论

3.1 切屑形态的预测

模型对Calamaz等的实验条件[17]进行数值模拟，刀具切削前角为0°，刀尖圆弧半径为20 μm，工件尺寸为 0.5 mm×1 mm，刀具切削速度为21～235 m/min，切削深度为 0.1 mm.图8所示为3种不同材料本构模型所产生的切屑形态，从图中可以看出：采用JC模型的切削模型并没有产生锯齿形切屑；采用JC损伤模型的切削模型虽然模拟出了锯齿形切屑，但切屑形态和实验结果相比并不规则，差别很大；而采用TANH模型的切削模型产生了与实际切屑形态相符并且比较规则的锯齿形切屑.

图9(a)所示为高速摄像机拍摄的实际切削过程，图9(b)所示为数值模拟结果，对比来看，该SPH模型很好地模拟出了刀具切削工件时剪切带和发生主要变形的区域.同时，该模型也很好地解释了锯齿形切屑的形成过程，如图10所示：

图8 不同本构的切削模型Fig.8 Different constitutive cutting models

(1)刀尖挤压工件，这时候在主剪切带，应力应变迅速增大，如图10(a)和(b)所示.

(2)随着刀具挤压增大，达到材料的屈服极限，材料的塑性变形开始发生，应变和应力继续增大，主剪切带开始向刀具前进方向滑移，见图10(c)和(d).

(3)随着刀具的继续前进，应力达到最大值后开始减小，材料发生再结晶现象，主剪切带发生滑移，产生锯齿形切屑，如图10(e)和(f)所示.

在本研究中，将切屑两齿之间的平均距离w以及齿高h1与h2作为衡量切屑形态的参量，并与实验结果进行比较，如表2所示.表2中：δi(i=h1,h2,w)为i的相对误差.

图9 切屑形态局部特征Fig.9 Local characteristics of chip morphology

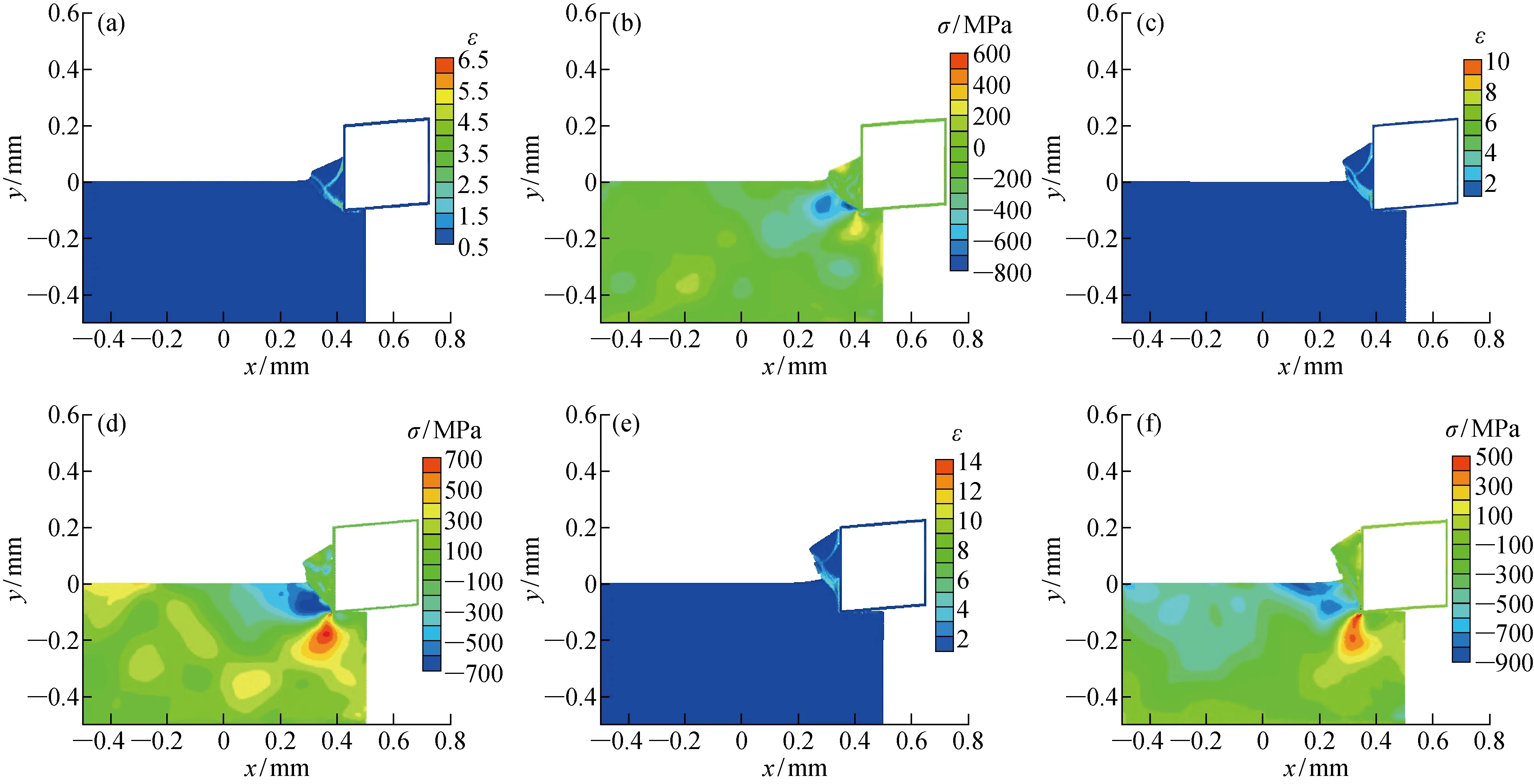
图10 切屑的形成过程Fig.10 Process of chips formation

表2 切屑形态模拟结果与实验之间的误差对比Tab.2 Comparison of errors in simulation chips morphology and experimental results

从实验结果与数值模拟的结果对比显示，基于SPH方法和TANH本构模型所建立的切削模型可以很好地对锯齿形切屑的齿高和齿宽进行预测，虽然存在误差，但考虑到切削是一个复杂的过程，受到实验环境、机床振动等客观因素的影响，该模拟结果的误差在可接受的范围内.

3.2 切削力预测

切削力是衡量切削模型准确的一个标准，因此，模型通过刀具表面粒子与工件粒子之间的相互作用来计算切削力，并将其输出.图11所示为刀具在切削速度为188 m/min,切削深度为 0.1 mm，时间长度为20 μs下切削力的变化.由图可见：切削力波动幅度较大，且呈现先增后降的周期性变化.形成这种变化的原因主要是由于刀具在切削钛合金工件时，随着刀具的前进，主剪切带应力应变突然增大，产生局部失稳并产生滑移，切削力也会随着主剪切带滑移而有一个瞬时的减小，随后在进入下一个锯齿形切屑的形成过程中，切削力又逐渐增大.

图11 不同时刻的切削力Fig.11 Cutting force with different moments

表3 切屑力模拟结果与实验之间的误差对比
Tab.3 Comparison of errors in simulation cutting force and experimental results

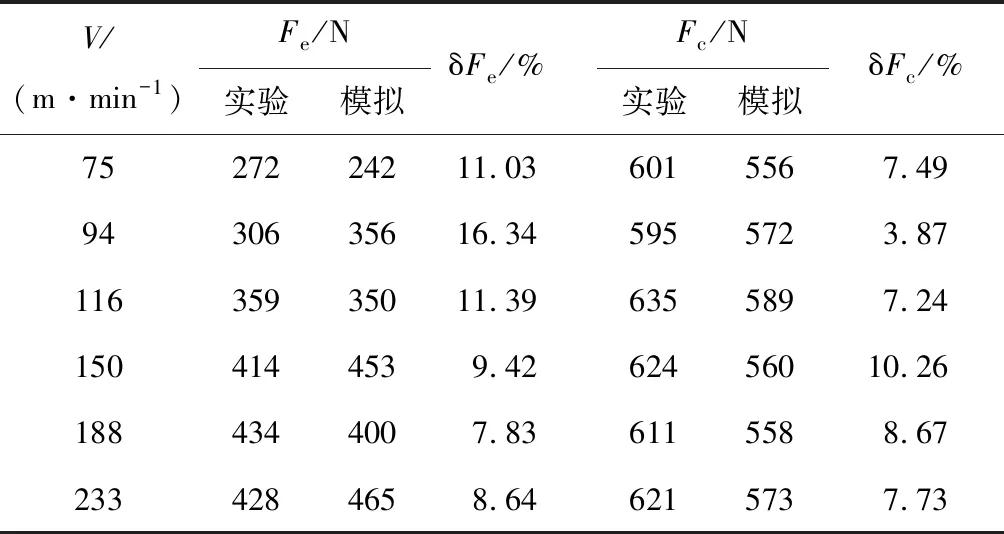
V/(m·min-1)Fe/N实验模拟δFe/%Fc/N实验模拟δFc/%7527224211.036015567.499430635616.345955723.8711635935011.396355897.241504144539.4262456010.261884344007.836115588.672334284658.646215737.73

表3所示为不同V下的平均切削力(Fc)和平均推挤力(Fe)的对比.其中：δi(i=Fc,Fe)为i的相对误差.结果显示，模型对切削力预测较为准确，但也存在一定的误差.误差原因可能为：① 数值模型均在理想切削条件下，并没有考虑人为因素(加工误差)、加工环境等影响；② 模型将刀具看成刚体，忽略了刀具变形以及磨损对切削力的影响；③ 模型没有将机床和刀具振动考虑在内，振动也会影响切削力的变化.

4 结语

上述研究表明，与传统有限元切削模型相比，基于SPH方法的切削模型解决了基于FEM传统的切削模型在切削过程中网格易发生畸变的问题，使模拟和计算结果更加准确.同时采用TANH本构模型对材料发生大应变情况下的动态力学性能进行描述，准确模拟出了钛合金在切削过程中产生的锯齿形切屑形态.通过与实验结果的对比，基于SPH方法和TANH本构模型所建立的切削模型模拟出的锯齿形切屑的齿高、齿宽以及切削力准确可靠.总的来说，该模型相较于大部分FEM的切削模型，有着如下优点：

(1)避免了网格畸变，很好地模拟出了切屑发生时大变形的部位，并且实现了切屑与工件的自然分离，不需要设置分离准则和删除网格.

(2)将钛合金材料在发生变形过程中的应变软化和材料再结晶现象都考虑在内，实现了切屑形态和切削力的准确预测.

目前研究无论是在切屑形态还是在切削力预测上都存在一定的误差，在未来的研究中可以针对文中所提到误差原因对模型进行改进，即将刀具变形或者刀具磨损因素考虑在内，并通过实验等方法测得刀具系统振动幅值与频率，根据这些实验数据对刀具设置振动等相关的边界条件，以此来准确模拟实际的切削过程.同时本模型只是基于二维的切削模型，今后三维模型的建模与分析也将是重点.