液滴在类刀-工-屑狭缝中的动态润湿特性
许 明,余 昕,倪 敬
(杭州电子科技大学 机械工程学院,杭州 310018)
随着切削液应用技术的不断发展,切削液的危害也被人们所认识,微量液体润滑(MQL)技术应运而生[1].与传统浇注切削液的方式不同,在使用MQL技术时,切削液往往是以孤液滴形式存在于前刀面,进而渗入刀-屑接触面起到润滑冷却作用.
刀具前刀面与切屑构成的狭缝是一个毫米-微米-纳米的跨尺度狭缝,切削液在狭缝中的渗透情况会极大地影响切削液的效用[2].因此,弄清楚液滴向不同高度微狭缝渗透的变化规律是十分必要的.Williams[3]建立了刀具-切屑界面间的毛细管网模型,提出切削液的渗透能力决定了它的效果,且效果随切削速度增大而减弱.Godlevski等[4]提出新的切削液渗透模型,将切削液的渗透分为3个阶段,提出了渗透过程中切削液的蒸发“爆炸”模型.文献[5-6]通过改变切削液对车刀的润湿性,改善了包括刀具磨损、加工速率、工件表面质量在内的加工参数.这些研究已经证明通过优化切削液的渗透能力可以改善加工参数,但是液滴向类刀-屑狭缝的渗透动特性却少有研究.现有相关研究主要关注流体沿微通道或微管道的一维流动,很少研究液滴在两平行板构成的微狭缝中的二维铺展特性.张雪龄等[7]对微纳圆管中的流体速度分布和流量等特性做了分析,发现尺度越小,体积流量偏离同尺度下泊肃叶流动的流量越大,当尺度降低到一定程度流体将不能流动.Ziarani等[8]考虑了微通道中粗糙度的影响,发现粗糙度的幅值、拓扑结构等特征会影响液体的压力梯度,随着压力梯度的增大液流的局部复杂度会随之增加.Bhardwaj等[9]利用晶格玻尔兹曼方法研究了不同黏度比对重力驱动下液滴在垂直平面上运动的影响,但其过程是由重力场驱动,而且是在平面上的运动而非狭缝.张明焜等[10]利用耗散分子动力学模拟完成了带凹槽微通道中液滴运动的数值模拟,但其模型中驱动液滴的力是外加力场,而且初始状态液滴就已经在通道内.Wang等[11]采用晶格玻尔兹曼法研究了粗糙度对液体在粗糙表面上非线性流动的影响.Randive等[12]采用两相晶格玻尔兹曼法对液滴在超疏水-亲水混合表面的润湿行为进行了研究,考虑了疏水表面毛管数和接触角等因素对液滴移动的影响,发现随着疏水表面毛管数的增加,整个表面的综合亲水性逐渐减小.
此外,现有相关研究通常使用的是足量流体,而对于体积固定的定量液滴的渗透特性却较少研究.对于有限体积的液滴而言,当所有液体都渗入狭缝后,由于表面张力等作用力的影响,液体不可能无限铺展.液滴的这一渗透及铺展过程较为复杂,涉及毛细作用力、空气和液体的表面张力、固体边界的吸附力和液滴的膜压等,因此很难对其渗透的动态过程进行建模分析.
尝试利用实验方法来对类刀-屑狭缝中液滴的动态润湿特性进行研究,利用一块透明石英砖和中间开槽的304不锈钢板构成类刀-工-屑的微米级狭缝,并采用图像处理技术,分析高速摄像机拍摄到的液滴向微米级狭缝中扩散铺展的动态过程,研究液滴扩散时的铺展特性以及与狭缝高度的关系.
1 实验
图1所示为切削液向刀屑界面的渗透过程示意.可以看出,切削液液滴渗入狭缝的过程十分复杂,是毫米-微米-纳米跨尺度下的毛细力、分子间力、黏附等相互作用的结果,很难直接对其进行建模及理论分析.

图1 切削液向刀-屑界面的渗透过程Fig.1 Penetration process of cutting fluid to tool-chip interface
1.1 实验材料及装置
采用石英片和304不锈钢板构造狭缝,微狭缝示意图如图2所示.表1所示为微狭缝特征参数.用H20光纤激光打标机在不锈钢板上雕刻时激光功率采用6 W可以得到较好的表面[13].而加工次数与打标的深度近似成正比关系.通过在实验样板上实际测试后,按比例增加打标次数,分别在标号为A、B和C的3块304不锈钢板上打出了平面尺寸为40 mm×60 mm,沟槽深分别为100、150和200 μm,为保证液滴铺展时不同高度狭缝内粗糙度一致,使用从220目到 7 000 目砂纸依次打磨雕刻后的不锈钢板,去除氧化层,降低粗糙度,最后用AT-01010抛光膏抛光,使其达到镜面效果,如图3(a)所示.而后拍摄了液滴渗入区域表面的形貌,如图3(b)所示.图3中:X和Y分别为液滴渗透区的位置;Z为渗透区各点与基准面的相对高度.实验中液滴为蒸馏水.
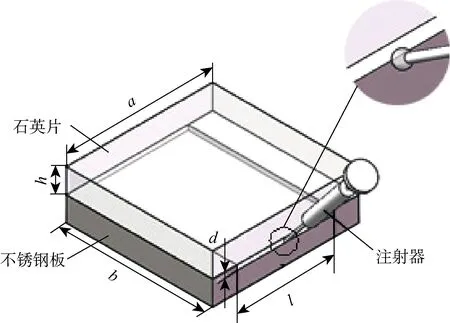
图2 微狭缝示意图Fig.2 Simulated micro-slit
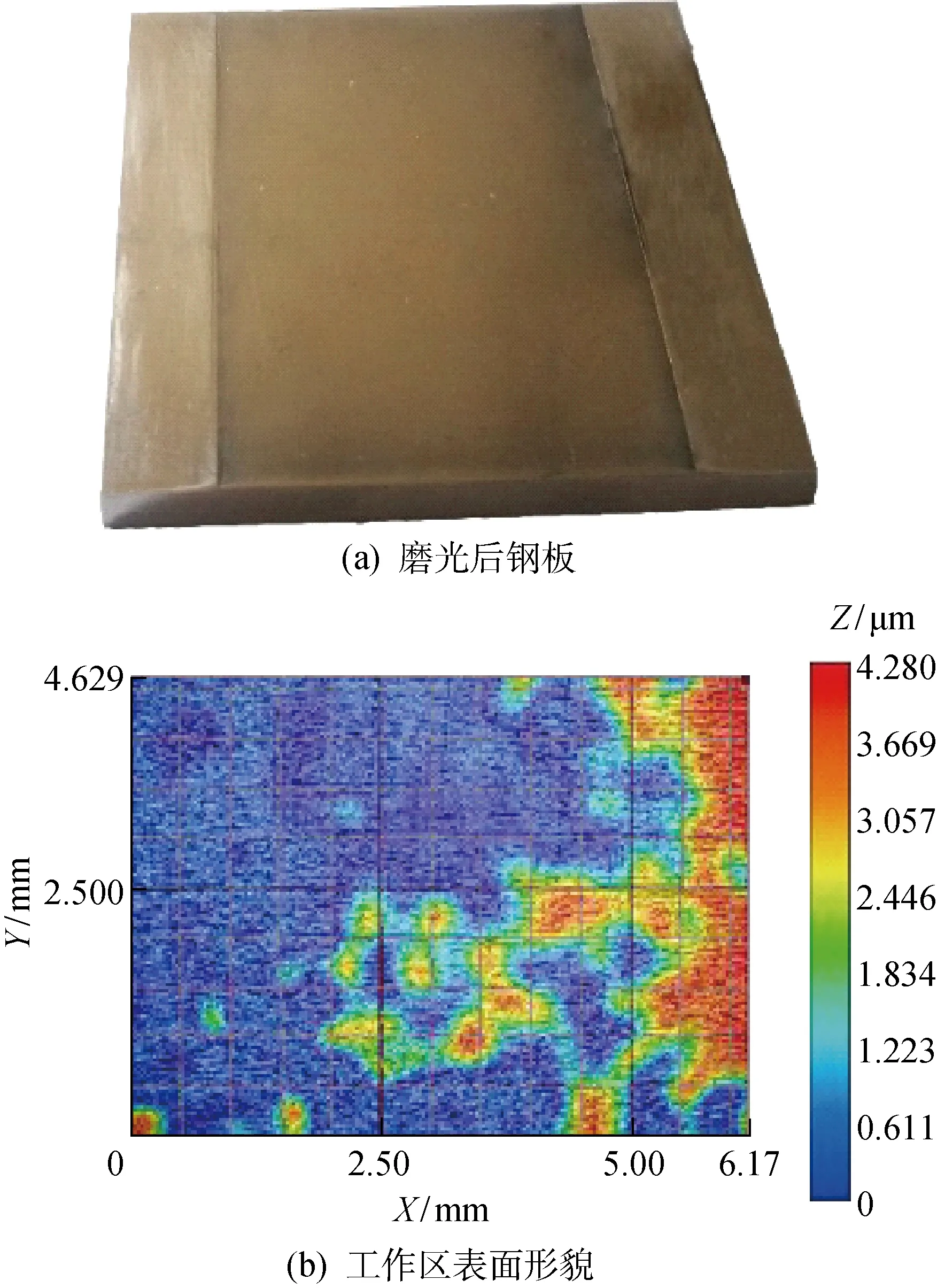
图3 钢板表面形貌Fig.3 Surface morphology of steel plate
1.2 实验步骤
将304不锈钢板A打磨抛光后的面朝上放置在摄像机(基恩士高速摄像仪,主机型号VW-9000,镜头型号VH-Z50L)载物台上,将石英板覆盖其上,在入口边对齐.为避免有过多的数据,导致对储存空间要求过高,因而将摄像机帧数设置为 2 000 帧/s,分辨率为640像素×480像素.由于狭缝高度d很小,即使液滴体积很小,在整个狭缝区域内也会铺展很大的面积.为了拍摄到尽可能大的扩散面积和尽量完整的铺展时间,将摄像机的倍数调到最小的×50档.用微升注射器汲取一定量水,并挤出约 0.5 μL,这时水会因为表面张力聚成球状黏附在注射器针尖.将液滴靠近狭缝,当贴近后,液滴便会由于毛细力的作用渗入狭缝区域,开始铺展过程.用高速摄像机记录下铺展过程,实验重复3次.
将304不锈钢板B和C按照A板过程同样分别做3次.得到在不同高度的狭缝中液滴扩散过程的视频,格式为AVI.
2 数据处理
2.1 数据处理方法
通过观察液滴铺展过程的视频发现,被液体占据的区域与干燥的区域相比亮度暗很多,如图4(a)所示.结合文献[14],采用图像处理方法,不需要在被测液体中添加示踪粒子,可以直接读取实验拍摄视频中的数据.

图4 图像处理效果图Fig.4 Image processing procedure
去除背景后采用均值滤波去除噪声,因为这种方法算法相对简单而且对盐噪声有很好的滤波效果.均值滤波后二值化处理效果如图4(b)所示,用OpenCV软件库自带的寻找轮廓函数画出轮廓如图4(c)所示.可以看到轮廓都是连续封闭曲线,因此只需要找出周长最长的那条轮廓并计算其围成的面积就是所求液滴覆盖面积,如图4(d)所示.
2.2 数据提取
将图像上每一个像素对应的实际面积作标定,得到每一个像素点对应实际64 μm2.遍历视频帧,统计白色像素点数量并与标定的比例值相乘,从而得到视频帧中液滴铺展面积S,选取3个高度狭缝实验中各一组,画出相应折线如图5所示.
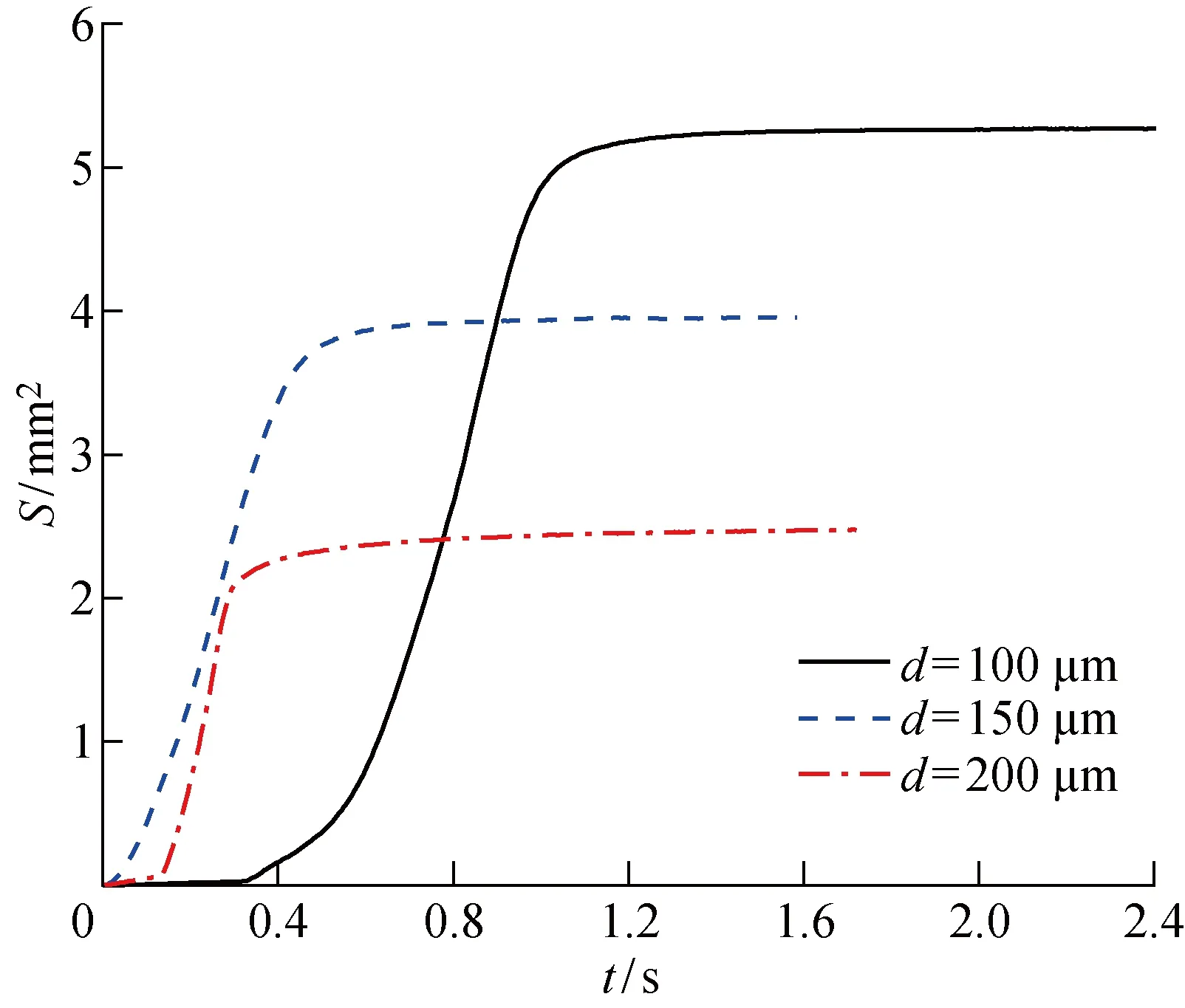
图5 铺展面积随时间变化Fig.5 Spread area changed with time
3 实验结果与分析
3.1 实验结果
由于3组实验的总水量相近,为了便于分析,将铺展面积转化为渗入狭缝中的水量,图6所示为不同狭缝高度下渗水量V随时间t变化.图中3条曲线分别表示3组实验.

图6 不同狭缝高度下渗水量随时间变化Fig.6 Variation of seepage volume with time at different slit heights
3.2 数据拟合及分析
液滴向狭缝扩散是一个典型的具有负反馈调节的动态过程,具有3个特点:
(1)在其他条件保持不变的情况下,影响铺展过程的因素只有铺展面积S和轮廓周长L的2个量.这是因为液滴的铺展是干燥的高能固体表面对低能液体的吸附力Fa和狭缝外气体及垂直固体面对液体的吸引力Fb共同作用的结果.其中:Fa正比于周长L;Fb与留在狭缝外的表面积正相关.
(2)系统只存在2个平衡点:① 狭缝中完全没有液滴的时候,这是一个不稳定平衡点,因为只要有一点点液体渗入,所有的液体都会全部渗入狭缝;② 液滴完全渗入狭缝,而这是一个稳定的平衡点,因为处于铺展的任一阶段都会最终到达完全铺展状态.
(3)只考虑动力学部分的话,系统不是能量守恒的,液体铺展过程中的动能转化为了吸附能,这是开始时刻固体表面能加液滴表面能与结束时刻固液界面能存在差值导致的.这部分吸附能以吸附热的形式耗散了.
以上特点都与Logistic模型相符合,Logistic 模型:
(1)
式中:K为渗入狭缝液滴的总体积;V0为液滴在狭缝中的初始体积,这部分液体产生了对液滴的初始吸引力;r为狭缝内部对液滴的吸引能力.
不同狭缝高度下渗透体积曲线的形状也符合Logistic模型的S型曲线,因此进行Logistic回归.以狭缝高度为200 μm的一组实验数据为例,令K为稳态值 0.492 7,保留2个参数V0和r作拟合,求得V0和r参数分别为 1.524 nL和 242.7,拟合结果如图7所示.
同样方法得到3种狭缝高度下各自3组曲线的Logistic模型拟合度及参数V0和r如表2所示.将各组的参数取平均后作出平均拟合曲线如图8所示,相应参数标在图中.
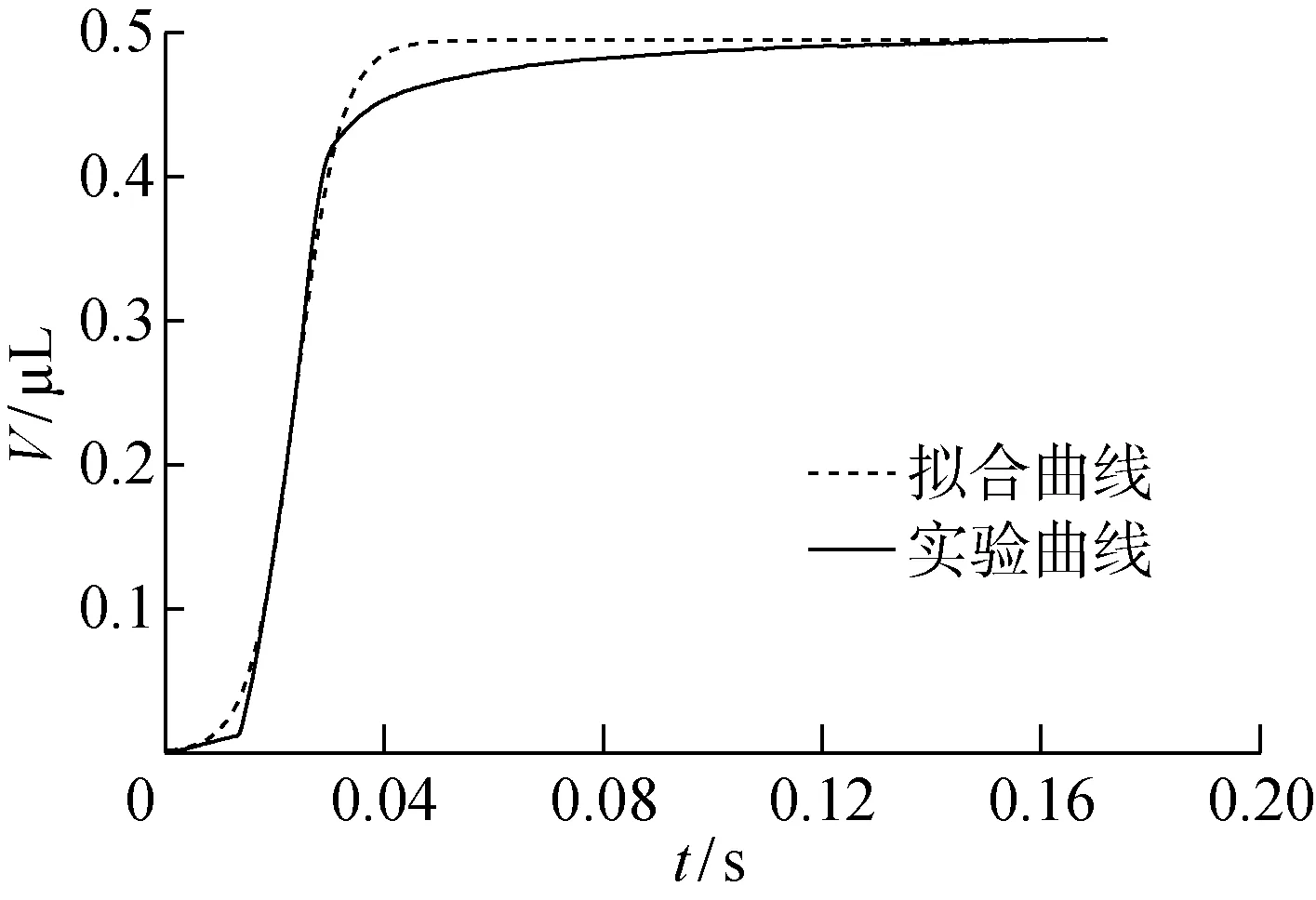
图7 Logistic拟合曲线Fig.7 Fitting curve of Logistic model
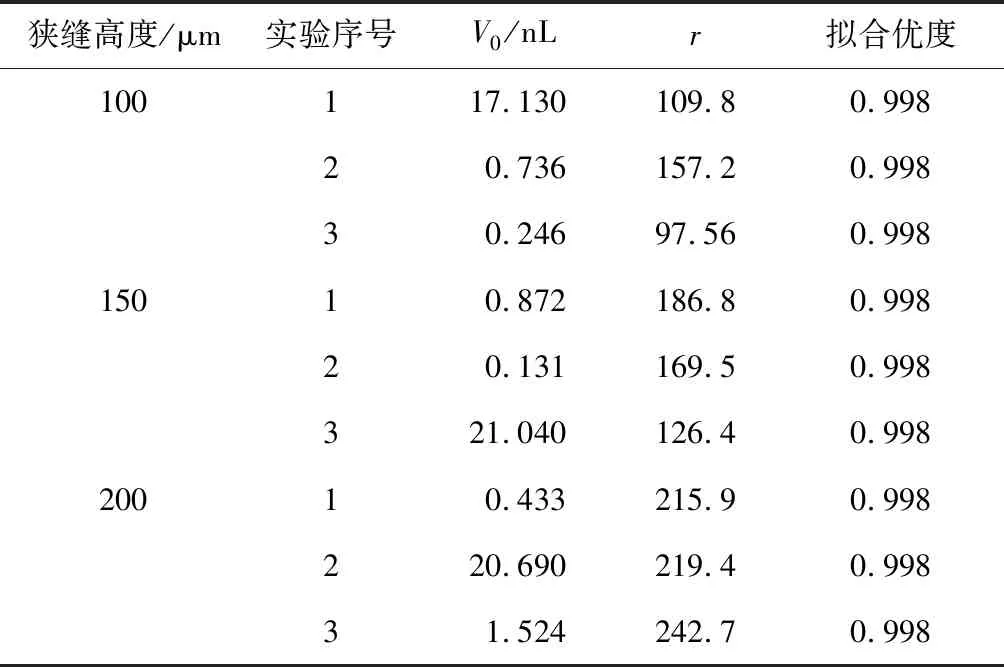
表2 Logistic模型拟合度Tab.2 Fitting degree of Logistic model
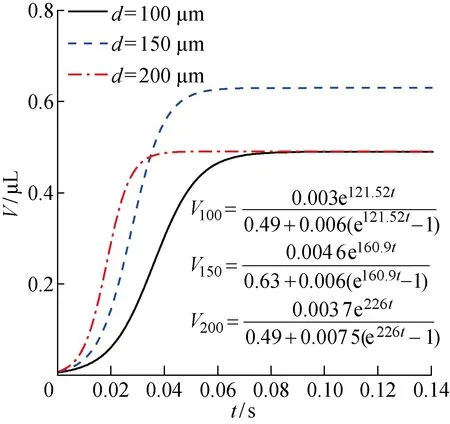
图8 3种狭缝高度的渗透体积Fig.8 Permeability volume of three kinds of slit heights
由图8可知,3条曲线的倾斜程度,以及拟合模型式(1)中代表增长速率的r值都是随着狭缝高度的增加而增大.
依照毛细管实验中计算毛细压力的方法计算狭缝中的毛细力,
F=2Lσ
(2)
(3)
式中:F为液滴在狭缝内受到的总毛细力;σ为单位长度的毛细力;pm为毛细压力;Sm为毛细力作用面积.
联立伯努利方程和流量连续性方程可得流量与压力差的关系:
(4)
式中:Q为渗透流量;Δp为渗透压力差;ρ为液滴密度.
式(3)中,Δp=pm.将式(2)代入式(3),可得
(5)
由式(4)可知,渗透流量随狭缝高度的增加而减小,这与实验结果刚好相反.之所以产生实验中现象,是狭缝高度的增加使得与毛细压力平衡的作用力也减小了,而这一减小的速度大于高度增加引起的流量减小速度.
4 结语
通过Logistics模型对液滴向类刀-工-屑狭缝中的渗透过程进行了拟合,模型中K描述了渗入狭缝液滴体积的终态;V0描述了与狭缝产生初始吸引作用的液滴体积,这部分液滴通常在接触的一瞬间就已经处于狭缝内部;r则描述了狭缝内部对液滴的吸引能力.液滴在深度200 μm以下的狭缝中铺展时,渗入狭缝的液滴体积随狭缝深度减小而减小,这说明尽管随着尺度缩小,毛细压力增加,但是渗入狭缝还是越来越困难.

