基于二项式-正态层次模型框架下比例的贝叶斯Meta分析方法及实现

张天嵩

Meta分析可以定量、科学地合成研究结果，已在许多科学领域取得革命性的成果，有助于建立循证实践、解决相互矛盾的研究结果问题[1]。经典的Meta分析是针对两种干预措施基于头对头(head to head)的直接比较，主要观察两种干预措施的效果差异，相关方法已较成熟。近年来，国内外出现大量的系统评价采用Meta分析方法合并比例(proportions)或率(rates)[2-6]，但这些文献均是基于经典的正态-正态层次模型(normal-normal hierarchical model，NNHM)，获得的结果可能会存在偏倚，实际情况下，某些比例或率等数据(如接近于0或1时)并不适用于该模型。本文介绍一种更适用于比例的Meta分析模型及方法，即二项式-正态层次模型(binomial-normal hierarchical model，BNHM)和基于该模型框架下贝叶斯Meta分析方法，并通过实例来介绍软件实现过程。

1 方法

1.1 研究数据 数据来源于2个研究。数据1：来自Saber等的Meta分析文献[4]，共纳入29个研究(所有研究比例均<0.3，5个研究比例为0)，观察Pipeline栓塞装置(Pipeline embolization device，PED)治疗颅内动脉瘤的不良反应，本文选取拟分析的数据为缺血性并发症测量结果。数据2：来自Pritz等的Meta分析文献[7]，共纳入14个研究(10个研究比例>0.7,2个研究比例为1)，观察高动力疗法(hyperdynamic therapy)治疗血管痉挛的疗效，以神经功能缺失的临床症状改善为治疗成功的标准。表1中“n”和“r”分别表示每个研究总人数和事件发性(缺血并发症或治疗成功)人数。

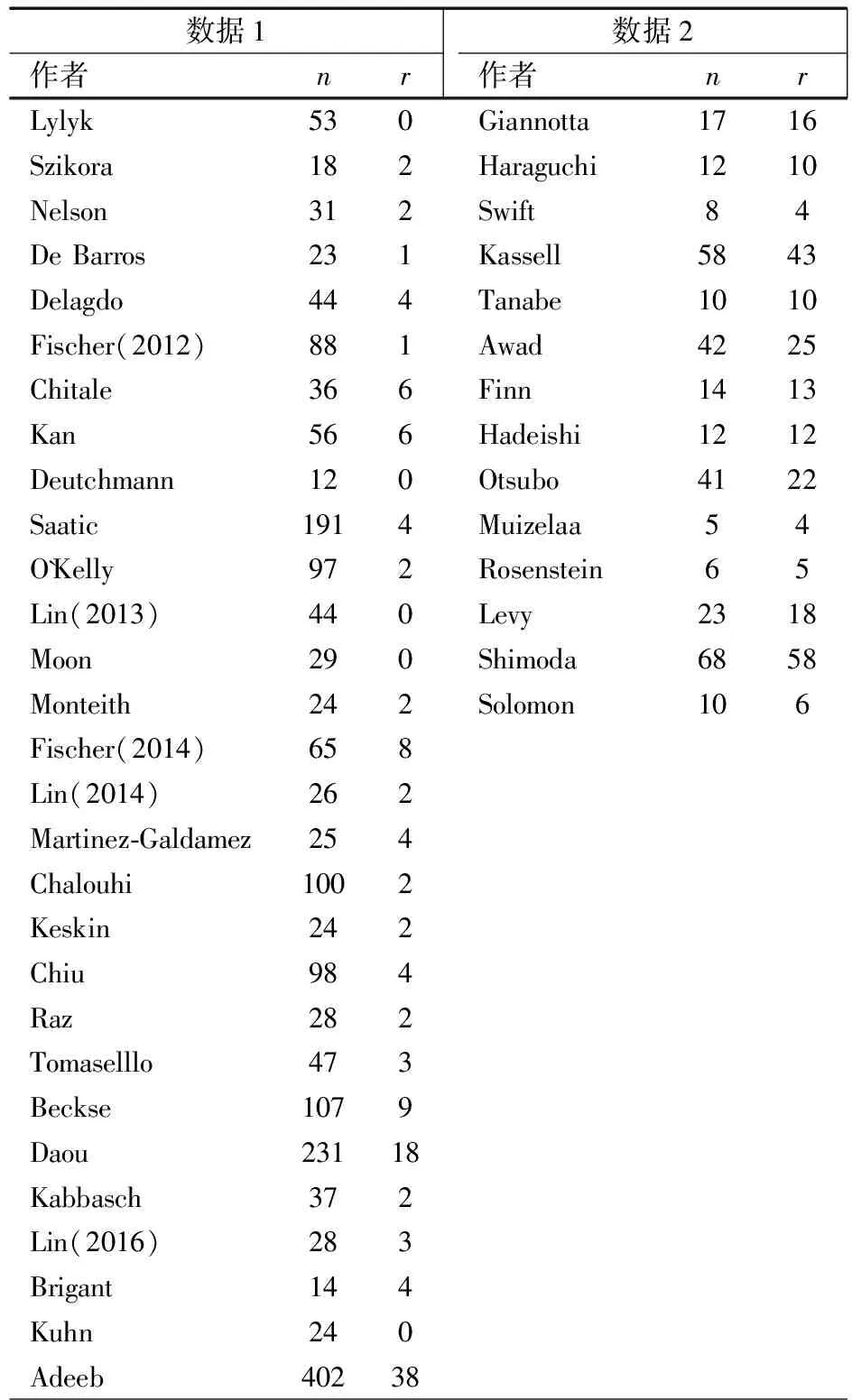
表1 分析数据

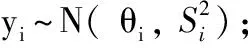
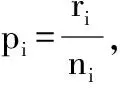
该模型可以SAS、Stata和R等软件来拟合。但在实践中会遇到很多问题[9,10]：①如果某些研究的事件发生比例很小(如接近于0)、或很大(如接近于1)，则抽样模型正态分布假设是否满足值得怀疑，且因研究估计值的方差会趋向于0，则该研究会得到一个很大的权重，计算所得的研究估计值95%CI可能会在[0,1]之外，此时需要采用logit转换法或双反正弦法等方法对数据进行转换；②当事件发生比例为0或1时，则方差为0，无法使用IV法计算，要对数据进行连续性校正，如对0格子数据加0.5。

在实践中，上述数据转换或连续性校正等方法均会导致结果偏倚。因此，有学者提出BNHM用于合并比例数据[8,9]，并给出了贝叶斯随机效应模型[11，12]，具体如下。

ri～Binomial(pi, ni)

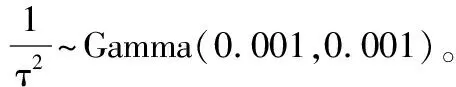
1.3 模型拟合 BNHM可由贝叶斯分析专用软件包来拟合，前期研究曾经给出了传统的贝叶斯分析软件WinBUGS实现该模型的代码[11，13]。针对实例数据，本文介绍新近比较流行的贝叶斯分析软件JAGS(ver4.3.0)联合R(ver3.4.4)实现该模型的拟合[14]，具体代码及简要解释见表2。通过R软件的R2jags扩展包来调用JAGS软件进行贝叶斯Meta分析，迭代50 000次，前20 000次用于退火以消除初始值的影响；采用收缩因子(shrink factor)进行收敛性判断，如果每个参数的收缩因子接近于1则认为马尔可夫链收敛[15]；mcmcplots扩展包绘制森林图(在BUGS语言软件中称为caterpillar图，实质上与Meta分析中森林图无异)；为了便于比较，本文同时采用R软件的meta扩展包来实现在频率学框架下拟合NNHM和BNHM，具体代码及简要解释见表3。

表2 比例的贝叶斯Meta分析代码(R软件)及简要解释

表3 比例的频率学Meta分析代码(R软件)及简要解释

2 结果

2个研究数据贝叶斯分析结果显示，每个参数的收缩因子(结果中Rhat值显示)都接近于1(结果从略)，表明马尔可夫链已收敛；不同数据贝叶斯方法获得的偏离信息准则(deviance information criterion,DIC)值分别为146.4和69.5，基于不同模型、采用不同分析框架和方法，随机效应模型获得的数字化结果见表4，基于BNHM，不论采用贝叶斯方法还是频率学方法，总的合并比例结果点估计及95%CI相差不大，但贝叶斯方法估计的研究间方差(τ2值)较大；基于NNHM获得合并效应量(点估计及95%CI)较BNHM结果相差比较大，特别是事件发生率小的数据(如数据1)；基于NNHM的算法获得的τ2值均较BNHM低，该模型低估了研究间方差。绘制森林图(图1和2)，图中所示细线表示各个研究和总的合并结果的95%CI，粗线表示后验分布的上、下四分位数间距离。

表4 基于不同模型、不同分析框架下Meta分析结果

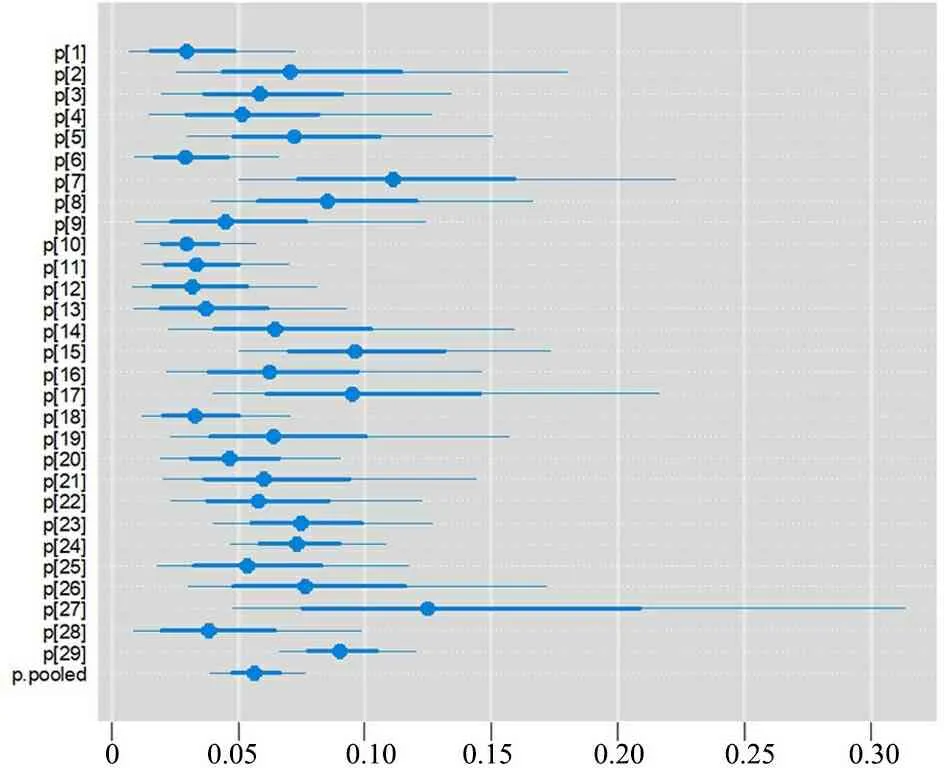
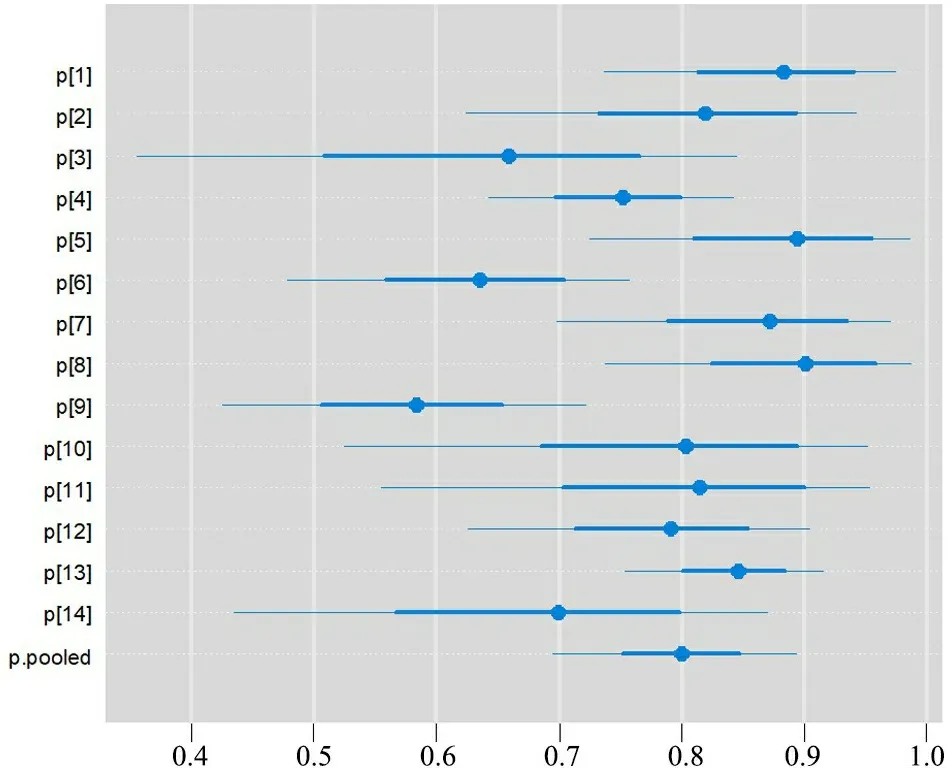
图1 数据1森林图(caterpillar图)

图2 数据2森林图(caterpillar图)

3 讨论

单臂研究在医学研究中较为常见，所获得的观察指标按资料性质可以分为定量资料和定性资料，其中比例即是常用的定性资料指标。所谓比例是指某事物内部各组成部分的观察单位数与所有组成部分的总观察单位数之比，可以表示分布结构的比例，也可以表示现象发生的频率，与观察时间单位无关，医学统计学中有很多相对指标被称为“率”，但实质上是“比例”，如患病率就是符合比例定义，但名称为率[11]。

目前发表的众多关于比例的系统评价文献多是基于NNHM，在频率学框架下采用IV法合并。一般认为，如果每个研究总样本量ni足够大(如>100)，nipi与ni(1-pi)不太小(如均>5)，则可以直接采用IV法合并；如果pi>0.7或pi<0.3则需要对数据进行转换[11]，常用的方法有Freeman-Tukey转换[16]及logit转换等方法，这些方法均可由Stata软件的metaprop命令及R软件的meta包和metafor包等轻松实现。如果比例为0或1的研究，则方差为0，采用直接合并数据或进行logit数据转换后再合并，均需要对数据进行连续校正，一般情况下各种软件默认加0.5校正，这样会高估或低估合并结果；而双反正弦数据转换(也称为Freeman-Tukey转换)不需要校正，但如果纳入Meta分析的研究总人数<10个(如数据2)，双反正弦数据转换后合并的结果再返回比例时，则有可能出现误导性结果。本研究发现，无论是否进行数据转换，NNHM会明显低估研究间方差；且如果研究比例接近甚至达到0或1，该模型估算可信区间会出现偏倚，这与Hamza等[10]模拟研究结果完全一致。

模拟研究表明，在大多数情况下，BNHM表现优于NNHM，可以获得无偏倚点估计及合适的置信区间[10]。该模型实质上是广义线性模型，可以在频率学和贝叶斯框架下实现，即使比例为0或1，也不需要进行连续校正，前者可以使用R软件的meta包和metafor包等频率学软件包来实现，后者可以通过WinBUGS、OpenBUGS、JAGS和Stan等贝叶斯软件包来实现。R软件中有不少扩展包，如R2WinBUGS、R2OpenBUGS、R2jags、rstan等，可以分别调用WinBUGS等贝叶斯软件包，则操作更灵活、显示结果更丰富。贝叶斯统计方法综合未知参数的总体信息、样本信息及先验信息，根据贝叶斯定理，获得未知参数的后验分布，进而对未知参数进行统计推断，目前已广泛应用于复杂数据的Meta分析(如网状Meta分析等)。本文是在综合了前人研究工作基础上，就如何合并比例数据，提供了基于BNHM框架下的贝叶斯Meta分析方法，因为Meta分析中固定效应模型假设研究之间具有同质性，但实际上一般很难成立[17]，本文使用的研究数据也证明了这一点，表4和图1、2显示，无论贝叶斯还是频率学框架，各种不同模型的分析结果均说明，纳入Meta分析的研究间均存在较大的异质性，因此本文是基于更为合适的随机效应来建模，并以2个特殊、但在实践中却是常见的数据类型为例，提出R软件实现方法。事实上BNHM模型总优于NNHM模型，NNHM在很多情况下不适用[10]，因此，在Meta分析时应优先使用BNHM。在实践中，贝叶斯方法对先验信息的利用和指定非常重要，贝叶斯Meta分析的先验分布可以允许利用先验信息确定，但在先验信息或知识缺乏的情况下，可以按下列方法处理：对绝对或相对效应测量(位置参数)选择指定无信息或模糊正态先验分布[18]；对研究精度指定为伽马先验分布，或对研究间质异质性指定为均匀先验分布。请注意，任何基于马尔可夫链蒙特卡罗(Markov Chain Monte Carlo，MCMC)的推断都是在假定马尔可夫链已经到达稳定状态(收敛)下进行的，因此，收敛性诊断是MCMC算法非常重要的问题[19]，本文采用的是收缩因子法， 还可以通过观察Gibbs动态抽样图、迭代历史图、抽样自相关图以及参数后验分布的核密度估计图等，判断马尔可夫链否收敛。

需要指出的是，在频率学框架下，比例的置信区间估算有简单近似法、连续相关校正简单近似法、得分法、连续校正得分法、精确法等方法[11]，多数教科书多推荐精确法，但鉴于精确法比较保守，有研究模拟显示在某些时候近似法较精确法为优[20]；而贝叶斯框架下，比例的可信区间则来源于未知参数的后验分布。

基于以下优点，针对比例进行Meta分析，本文推荐使用基于BNHM框架下的贝叶斯方法，其优点包括：①建模灵活，并在贝叶斯分析软件中可实现性强；②充分考虑了模型中参数(如方差等)的不确定性，合并效应量点估计及95%可信区间来源于参数的后验分布，结果可靠；③二项式似然允许有0格子数据，所以即使有研究的比例为0或1，也不需要与经典频率学方法一样对数据进行连续性校正。