多线性极大算子在Orlicz空间的弱有界性估计
张友朋,陶祥兴
(浙江科技学院 理学院,杭州 310023)

1 预备知识
1.1 定 义
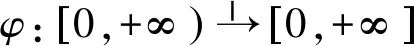
1)φ(0)=0;
2)存在0 4)φ是凸函数。 这样定义的函数φ有以下一些简单结论: 1)允许φ取到+∞; 2)不要求φ是严格凸函数或是严格单调递增函数;但是,当φ在有限点x0处取到+∞时,φ(x)必须在x充分大时严格单调递增; 3)φ(∞)=∞; 4)要么φ在[0,+∞)是连续的,要么存在0 容易看出,当φ(x)=xp(1≤p<∞)时,Lφ=Lp。 Orlicz范数有以下一些简单特征和结论。 1)Orlicz范数是一个范数。它满足正齐次性,‖αf‖φ=|α|‖f‖φ;满足正定性,‖f‖φ=0当且仅当f=0;满足次可加性,若‖f1‖φ=λ1,‖f2‖φ=λ2,则有‖f1+f2‖φ≤λ1+λ2。 2)若φ1和φ2是两个Young函数,且φ1≤φ2,则有‖f‖φ1≤‖f‖φ2。因此,若存在正常数a,b使得φ1(ax)≤φ2(x)≤φ1(bx)对所有的x成立,则Lφ1=Lφ2。 3)若φ1和φ2是两个Young函数,则φ≡φ1+φ2是一个Young函数,且Lφ=Lφ1∩Lφ2。 令(X1,v1)和(X2,v2)为正可测空间,算子T定义在X1上的v1可测函数集的一些线性子空间,值域包含在X2上的v2可测函数集里,若存在常数c≥1使得 |T(f+g)(x)|≤c(|Tf(x)|+|Tg(x)|)且|T(λf)(x)|=|λ||Tf(x)| 对所有算子T定义域里的f和g,对所有的λ∈R成立,则称算子T是线性算子[13]。 令A和B为Young函数,T为定义在LA(X1,v1)上的单线性算子,则 1)若存在正常数k使得 ‖Tf‖LB(X2,v2)≤k‖f‖LA(X1,v1) 对所有的f∈LA(X1,v1)成立,则算子T称为强(A,B)型的; 2)若存在正常数k使得 对所有的t>0和所有的f∈LA(X1,v1)成立,则算子T称为弱(A,B)型的。 我们可以将其推广到双线性算子,甚至是多线性算子。 令A1,A2和B为Young函数,T为定义在LA1(X1,v1)×LA2(X1,v1)上的双线性算子,则 1)若存在正常数k使得 ‖T(f1,f2)‖LB(X2,v2)≤k‖f1‖LA1(X1,v1)‖f2‖LA2(X1,v1) 对所有的f1∈LA1(X1,v1),f2∈LA2(X1,v1)成立,则称算子T为强(A1;A2,B)型的; 2)若存在正常数k使得 对所有的t>0和f1∈LA1(X1,v1),f2∈LA2(X1,v1)成立,则称算子T为弱(A1;A2,B)型的。 文献[13]分别给出了分数次极大算子Mα以及分数次积分算子Iα在Orlicz空间里的弱有界性估计和强有界性估计。这里引用了其中的分数次极大算子Mα的弱有界性估计。 引理1[13]令n≥1,且0≤α 成立,当且仅当存在常数c满足 引理2若算子Gi为(pi,qi)型,即 ‖Gif‖Lqi,∞≤c‖f‖Lpi, 则 证明:不妨证i=2的情况。∀β>0,有 故 引理2证毕。 这是当算子Gi为(pi,qi)型时成立,则当算子Gi为弱(pi,qi)型时也成立,故引出了下面的命题1以及定理1。 命题1设 对任意的r>0成立。 由于 定理1设Ai(i=1,…,m),B是Young函数,0≤α 成立,当且仅当存在常数c2满足 命题1的证明: 另一方面, 故 从而 命题1得证。 定理1的证明:充分性的证明同命题1的证明。下证必要性。 即 定理1证毕。 本文给出了多线性分数次极大算子在Orlicz空间的弱有界性,在今后的研究中可探究多线性分数次极大算子在Orlicz空间的强有界性以及其他多线性算子的有界性。
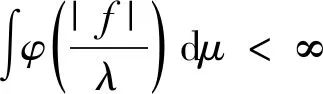



1.2 引 理


2 主要结论

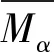
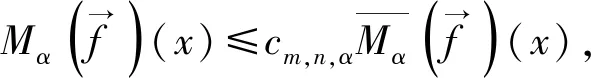






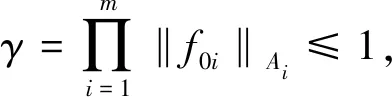
3 结 语

