水蒸气压强对空气管内强制对流传热系数的影响

诸爱士，金婉梅，李倩竹，赵军子

(浙江科技学院 生物与化学工程学院，杭州 310023)

传热现象普遍存在于自然界和工程领域，与人们的生活和生产活动等有着密切的联系，在日常生活和工业活动中发挥着重要的作用。传热方式有导热、对流和辐射三种，而在许多场合中不是单独存在的，是多种方式组合发挥着作用。在工程领域的研究、生产中，为了给流体加热或冷凝、冷却降温，往往采用间壁式换热器，工业上广泛应用的一种形式是管壳式换热器[1]。其中，热量通过推动力——温度差从流体传至壁面或由壁面传至流体的对流传热方式占据优势。对流传热又分自然对流和强制对流，其中强制对流是常用的方式。对流传热的关键是对流传热系数，目前研究的热点是传热体系、流动状态、传热表面状况、操作压强等对对流传热系数测定与关联的影响[2-8]。在实验教学中出现过壳程加热蒸汽压强是否会对管程空气对流传热系数测定有影响的问题，但结果鲜见报道。因此本文研究了加热水蒸气操作压强(水蒸气温度)对空气在圆形直管内强制对流时的传热系数的影响，同时考察了试验在同一装置与不同装置上的重现性，以此来说明试验和关联方法的合理性，以求为实验教学寻求明确的答案，也可为工程应用提供依据。

1 试验原理与研究方法

图1 间壁式换热原理Fig.1 Schematic diagram of dividing wall type heat transfer

间壁式换热其热量传递交换是由冷、热流体的热量通过传热元件的壁面而实现。如图1所示，整个换热过程可分为三部分，即热流体经对流将热量传递到壁面、壁面经导热将热量由高温侧传递到低温侧、经对流将热量由壁面传至冷流体[9-10]。

在本研究中，热流体采用水蒸气，冷流体采用空气，因此该过程属一侧恒温相变一侧变温的换热过程，当两者达到传热稳定时，忽略设备热损失，则有

(1)

式(1)中：Q为传热量，J/s；ms1、ms2分别为参与换热的水蒸气、空气的质量流量，kg/s；r为水蒸气在操作压强(饱和温度)下的冷凝热，J/kg；cp2为空气的比热，J/(kg·℃)；T为水蒸气的饱和温度，℃；t1、t2分别为空气在换热器进口、出口处的温度，℃；α1为水蒸气冷凝传热系数，α2为空气的平均对流传热系数，W/(m2·℃)；A1、A2分别为水蒸气侧、空气侧的传热面积，m2；TW、tW分别为水蒸气侧与空气的壁面温度，℃；(T-TW)m、(tW-t)m分别为水蒸气与壁面间、壁面与空气间的对数平均温度差，℃；K2为基于传热面积A2的总传热系数，W/(m2·℃)；Δtm为水蒸气与空气间的对数平均温度差，℃；其中Δtm可由式(2)计算：

(2)

研究中采用的装置为套管式换热器，空气走内管，水蒸气走管隙，即内管为传热管。详细的试验装置构成及流程见图2。

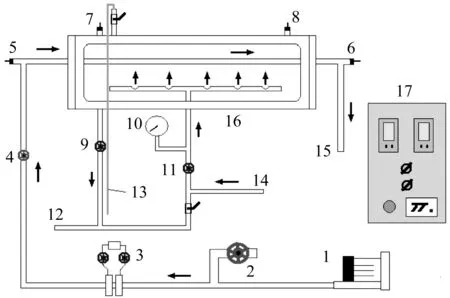
1—旋涡风机；2—空气旁路阀；3—孔板流量计；4—空气进口阀；5—进口端空气温度计；6—出口端空气温度计；7—空气进口侧水蒸气温度计；8—空气出口侧水蒸气温度计；9—冷凝水排出阀；10—水蒸气压强表；11—水蒸气进口阀；12—冷凝水排出管；13—不凝性气体排空管；14—水蒸气进口管；15—空气出口管；16—套管换热器；17—仪表控制箱。图2 试验装置Fig.2 Diagram of experimental devices

试验中传热管的长度l和内径d2已给定，传热面积即为A2=πd2l，如再测出tw、t1与t2以及空气的体积流量Vs2，即可由Vs2=ms2·ρ计算得到空气的质量流量ms2，进而可由式(1)计算得到α2。但是，试验中直接准确测定传热管内表面的壁温难以实现，如测出也不够准确，会使试验误差较大。因此，试验中改用能方便测定的空气、水蒸气的温度，进而来间接推算出空气与壁面间的对流传热系数，这是一种广泛被采用的研究手段。

根据式(1)可以导出：

(3)

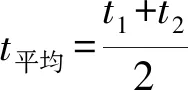
基于A2的总传热系数K2的关联式为：

(4)

式(4)中：d1、d2、dm分别为传热管外径、内径、对数平均直径，m；b为传热管的壁厚，m；λ为传热管材料的导热系数，W/(m·℃)；Rs1、Rs2分别为传热管外侧、内侧的污垢热阻，(m2·℃)/W。

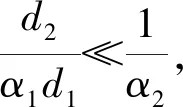
α2≈K2。

(5)

因此，若式(4)中被忽略的各项热阻与空气侧对流传热热阻相比越小，则该方法所得的结果越准确。

由于流体湍流时对流传热系数大，对传热有利，所以在工程应用中尽量使流体处在湍流区进行对流传热。在圆形直管内流体湍流时的对流传热系数关联式使用最广的经验式是迪图斯-贝尔特公式，即

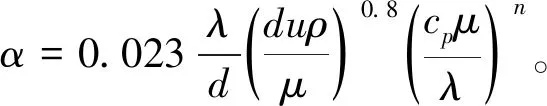
(6)

式(6)中：Nu为努瑟尔特准数，Re为雷诺数，Pr为普兰特准数，三者均无因次；d为管道内径，m；当流体被加热时，n=0.4；当流体被冷却时，n=0.3。式(6)的使用有一定的条件范围，可以参阅文献[11]189。

本研究将湍流区的试验结果先以ln(Nu/Pr0.4)-lnRe作图，并按经验式形式进行关联[12]，得到如式(6)形式的关联式，并与经验式Nu/Pr0.4=0.023Re0.8进行比较。试验步骤如下：打开总电源、仪表开关；开蒸汽发生器电源，加水加热，恒压保温；开风机，开冷流体进口阀，控制空气流量；开冷凝水出口阀控制开度；换热器通水蒸气，打开顶端放气阀排除套管内空气；控制水蒸气阀的开度，保持操作压强；观察系统状况，待水蒸气温度稳定、风量稳定后，等待一定时间，读取参数值(Vs2、t1、t2、T)；维持操作压强，改变风量，测定5组试验数据；改变条件(水蒸气压强或装置)，重复试验；完成数据处理与分析。

2 结果与讨论

2.1 不同水蒸气压强的影响

在同一装置上，选取0.01、0.02、0.03、0.04、0.05、0.06、0.1 MPa的水蒸气操作压强分别进行试验，对试验数据进行拟合，并与经验式进行比较，各压强下的试验点及趋势线汇总于图3，数据结果汇总于表1。

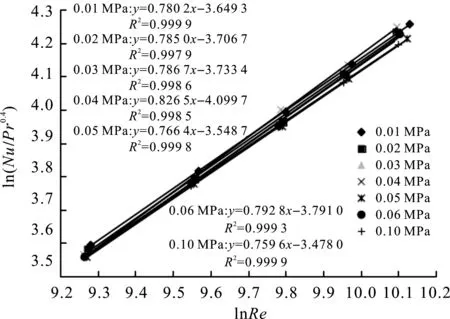
图3 湍流区各压强下试验值Fig.3 Experimental values at various pressures in the turbulent flow region

由图3可知，同一台装置在不同水蒸气操作压强及同一风量下所测得的结果相近，7条拟合线交织在一起，各个压强之间的拟合直线重合度较高。虽有差异，但看似不大。存在的差异可能由于室内环境温度变化、仪表参数(压强、风量)显示不准、操作偏差等引起。

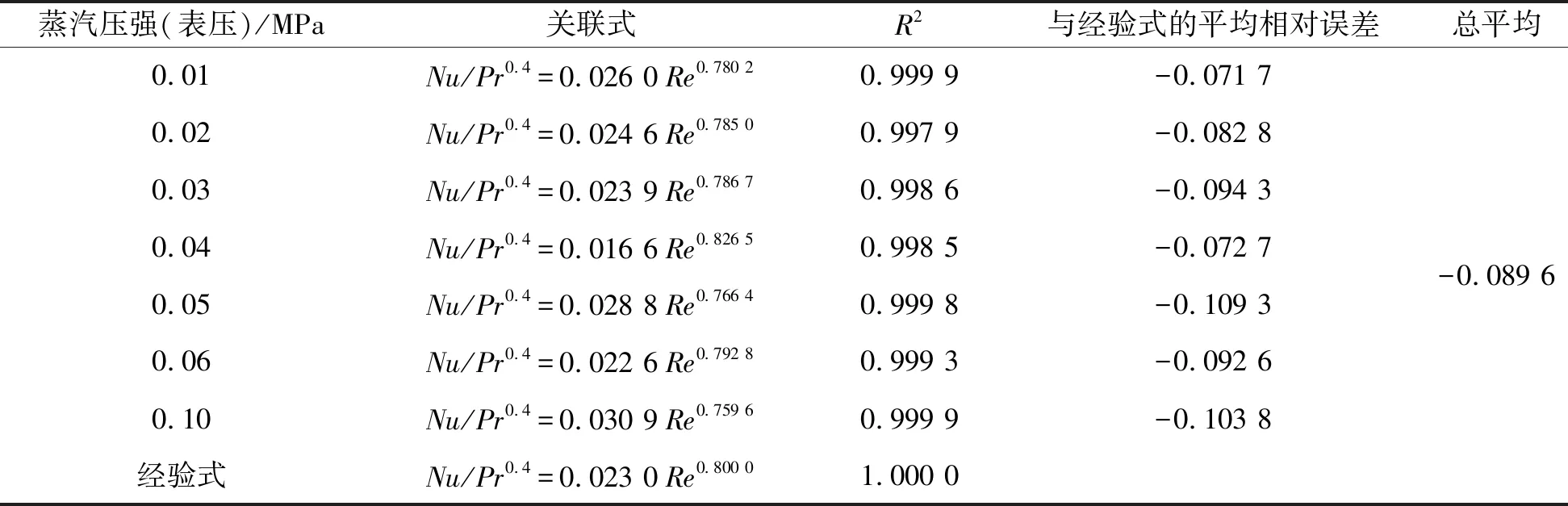
表1 各压强下的关联式Table 1 Correlations at each pressure

从表1中数据可以发现，在不同水蒸气操作压强下，试验值均低于经验值，与经验值的平均相对误差相近，相差10%左右，但总体上有增大的趋势；总平均相对误差为-8.96%；实际应用时，如以经验式计算对流传热系数，则需考虑修正，修正系数可取0.92。误差的原因是计算方法、装置参数显示等，特别是风量的校正导致经验式使用的风速比实际风速大，从而使Re数偏大、经验值增大。

为检验压强影响的显著性，进行了无重复双因素方差分析(一个因素是压强，一个因素是Re)，数据取值见表2(表中数据为相应Re的Nu/Pr0.4值，表4同)，分析结果见表3(F检验的置信度为0.05，下同)。

表2 无重复双因素方差分析选择数据Table 2 Selecting data of no repeated two-factor variance analysis

表3 无重复双因素方差分析结果Table 3 Results of no repeated two-factor variance analysis

由表2可以看出，在相同的Re下，Nu/Pr0.4在不同的水蒸气压强下具有不同的值，且变化或小或大；但总体上在研究的压强范围内随着水蒸气压强增大Nu/Pr0.4在减小，不过变化量的绝对值不大；由表3数据可得，列的F>Fcrit，P<0.05，这说明加热水蒸气压强对结果影响非常显著。水蒸气压强的变化，即其温度发生变化，会使水蒸气侧的壁面温度发生变化，另一侧的壁面温度也随之而变，这样会影响壁面两侧的边界层温度，特别是空气温度的升高使其黏度增大，因此对空气的对流传热系数有一定影响。

2.2 试验重复性

在同一装置上，选择0.03 MPa的压强，再进行两次重复试验，试验时保证测量风量一致，共得到3组数据，试验结果如图4所示。

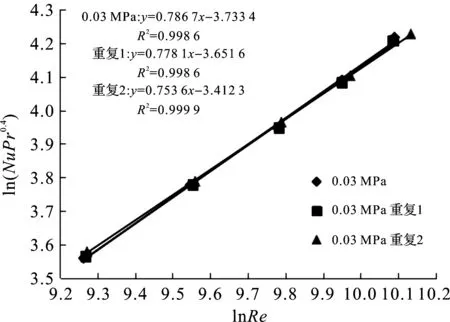
图4 装置1在0.03 MPa下的试验重复性Fig.4 Experimental repeatability of device 1 at 0.03 MPa

图4显示3次试验结果重合度较高。采用上述无重复双因素方差分析检验试验的重复性，数据取值见表4，分析结果见表5。

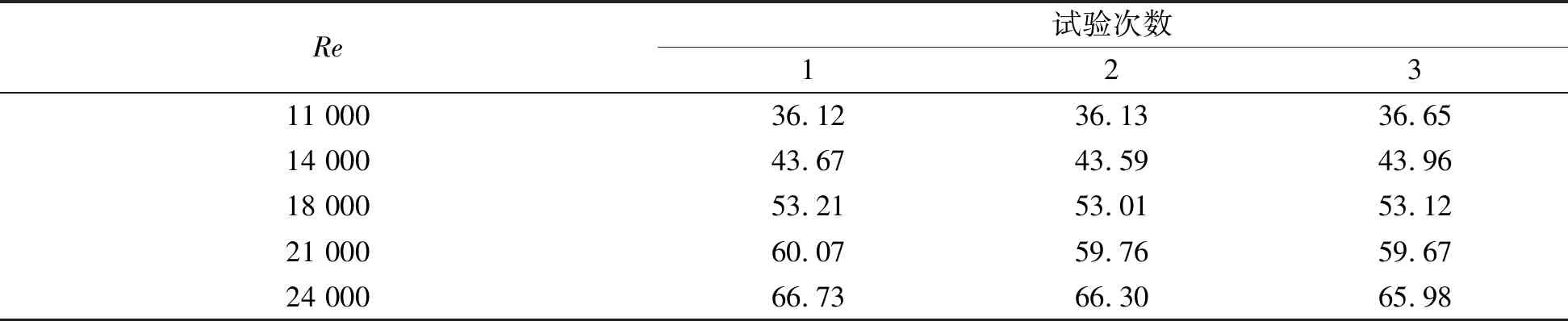
表4 0.03 MPa试验重复性检验取值数据Table 4 Selecting data of experimental repeatability test at 0.03 MPa

表5 0.03 MPa试验重复性检验结果Table 5 Results of experimental repeatability test at 0.03 MPa

由表4数据可得，列的F0.05，这说明不同试验的结果间没有显著差异，即试验重复性好。选择0.05 MPa的压强，再进行两次试验，然后对结果进行分析(具体数据、图、表省略)，得到类似的结论。这说明试验的重复性较好。

2.3 不同装置间的差异

在另一台相同型号的装置上，同样选取0.03 MPa的压强进行试验并多次重复，点、线结果见图5，分析结果见表6(表中数据为相应lnRe下的ln(Nu/Pr0.4)值)、表7。

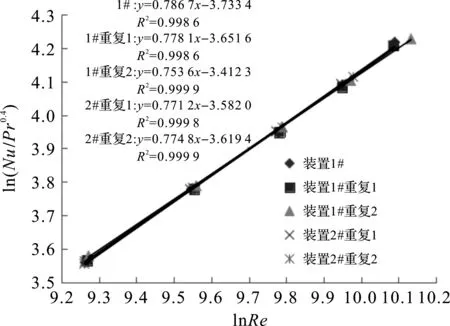
图5 0.03 MPa时装置2的重复性及其与装置1间的差异性Fig.5 Repeatability of device 2 and difference between device 2 and device 1 at 0.03 MPa

lnRe试验次数123459.33.582 93.584 73.596 23.590 23.586 29.53.740 33.740 43.746 93.744 43.741 29.73.897 63.896 03.897 63.898 63.896 29.94.054 94.051 64.048 34.052 94.051 1

表7 两装置0.03 MPa试验重现性检验结果Table 7 Results of experiment reproducibility test between two devices at 0.03 MPa

从图5看到，图中的5条拟合线几乎重合，直观上没有明显区别，这说明装置2的试验重复性好且与装置1间也没有明显差别；无重复双因素分析中，列的F0.05，这说明5组试验的结果无明显差别。同样进行了0.05 MPa时设备2的重复性试验和与设备1的差异性分析(具体数据、图、表省略)，得到类似的结果，即试验重复性好，设备间没有显著差异。

以上结果说明试验在不同装置上进行，其重现性高，对试验结果影响不大，具有一定的普遍性，即该测定和关联水蒸气加热的圆形直管内空气强制对流传热系数的方法是合理的。

3 结 语

本研究发现不同的水蒸气操作压强显著影响圆形直管内空气强制湍流的对流传热系数，试验值小于经验值，实际应用时应考虑其影响并适当进行校正，修正系数可取0.92；该试验在同一台装置上重复进行，结果没有明显差异，重复性好；在不同的装置上进行相同的试验，结果也没有显著差异，重现性好。因此，该对流传热系数的测定方法可靠，对传热理论与实验的教学也具有指导意义。