具有拟周期结构的两点边值问题的渐近展开法
舒 祥,何文明
(温州大学数理与电子信息工程学院,浙江温州 325035)
复合材料的静弹性分析、非均匀介质中的力学性能的评价等问题在数学上可以描述为区域上具有剧烈震荡系数的微分方程边值问题.在使用传统的有限元法和有限差分法求解该类问题时,由于ε很小,较难得到数值结果,且有可能破坏有限元方法的性能[1].针对复合材料弹性体的物理参数具有小周期结构的情况,文献[2-6]提出了一种称为均匀化的应用数学方法.考虑到实际问题,由于复合材料受到湿热和结构设计的影响,在许多情形下弹性体在整体上并不具有周期结构,而仅仅具有局部的小周期结构,因此本文将要对具有局部小周期结构的椭圆问题展开研究.为简单起见,本文仅考虑如下的具有拟周期结构的一维Dirichlet问题.
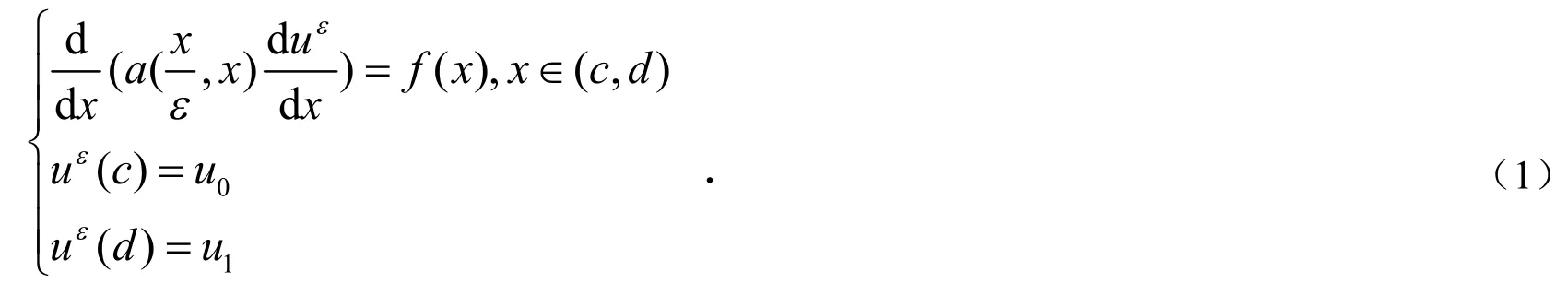
1 方程(1)的数值解法
利用渐近展开法本文得到了问题(1)的数值求解方法.首先我们将求解区间[c,d]均匀剖分为其中故对方程(1)按如下步骤求解:
b)得到方程(1)在任意点的数值解.
先来考虑a).我们注意到存在参数αi,βi,fi使得其中无关.下面先来考虑如何计算αi,βi.
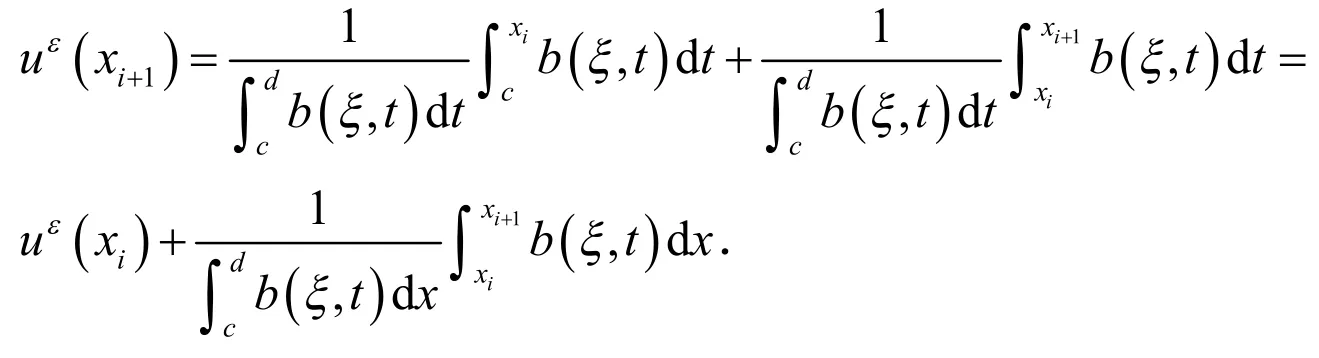
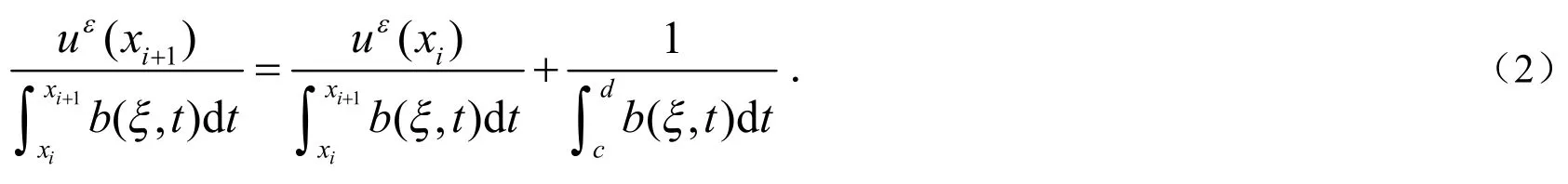
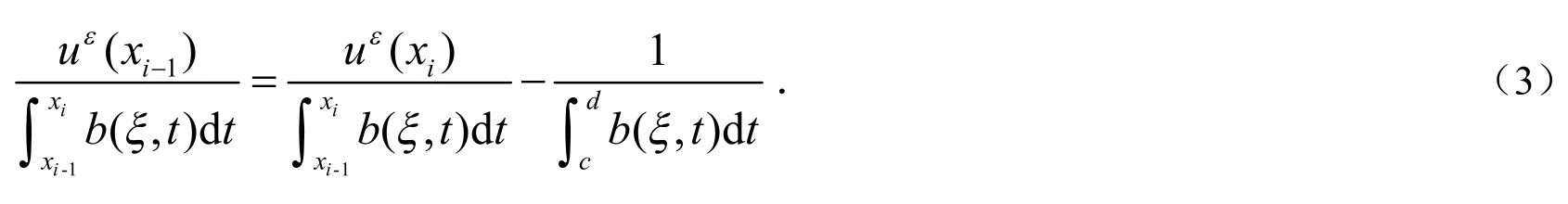
由(2)式和(3)式得:
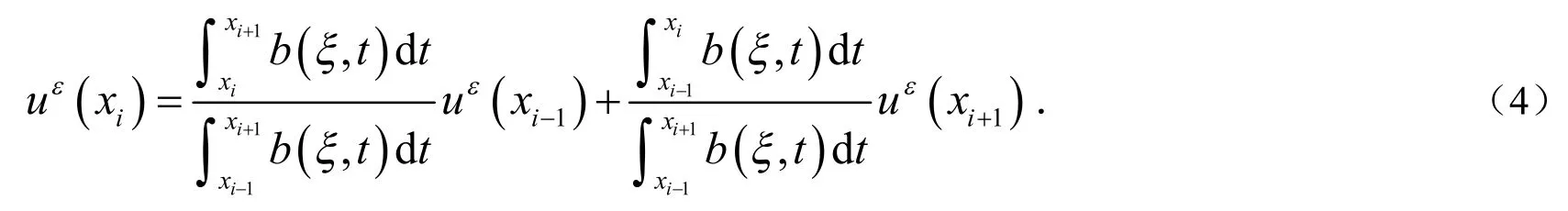
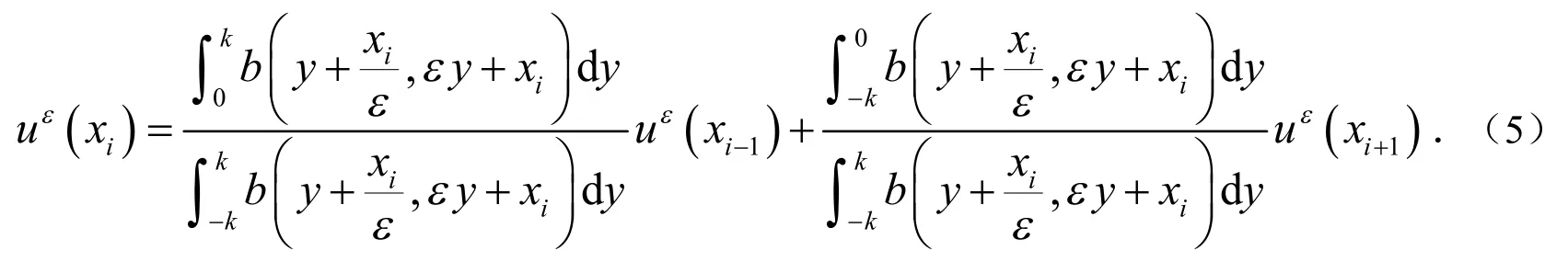
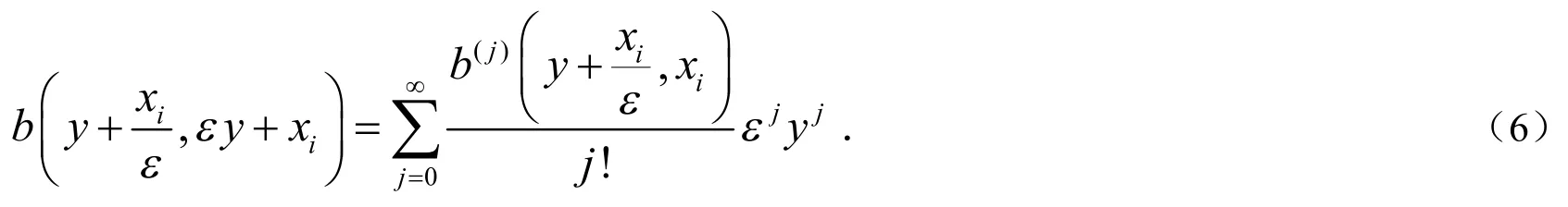
将(6)式代入(5)式得到:
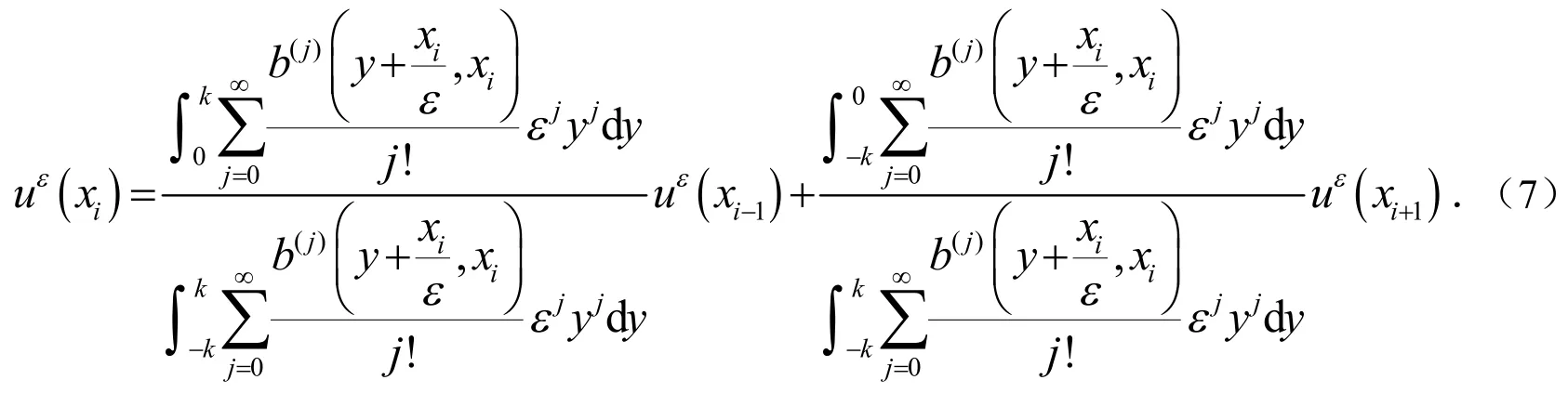
对任意的j≥0,令由(7)式得到:
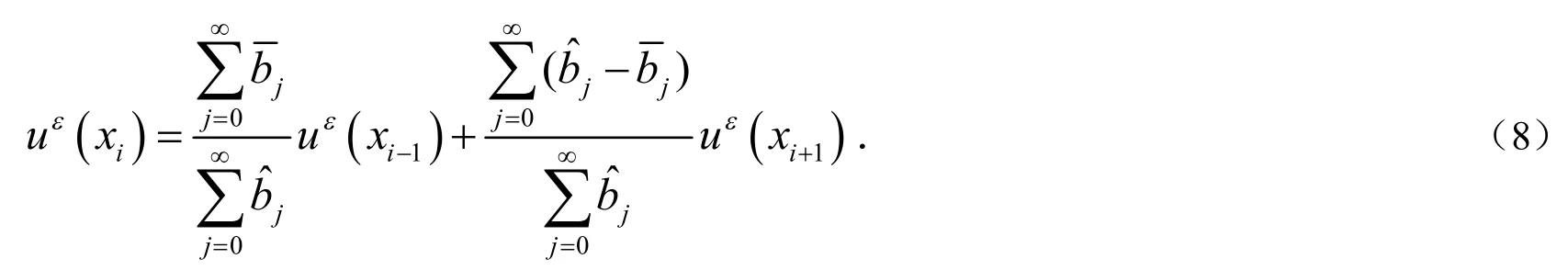
引理1 当f≡0时有:
下面考虑如何计算fi.

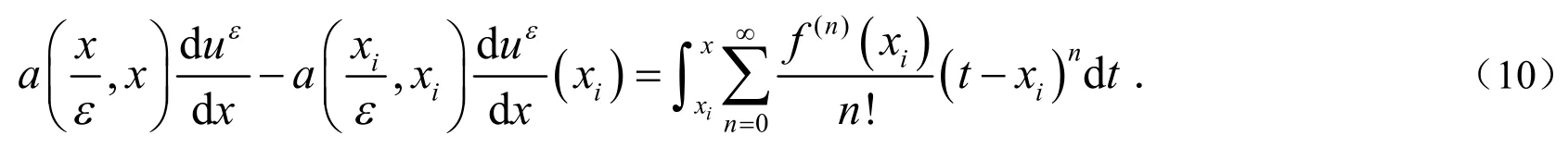
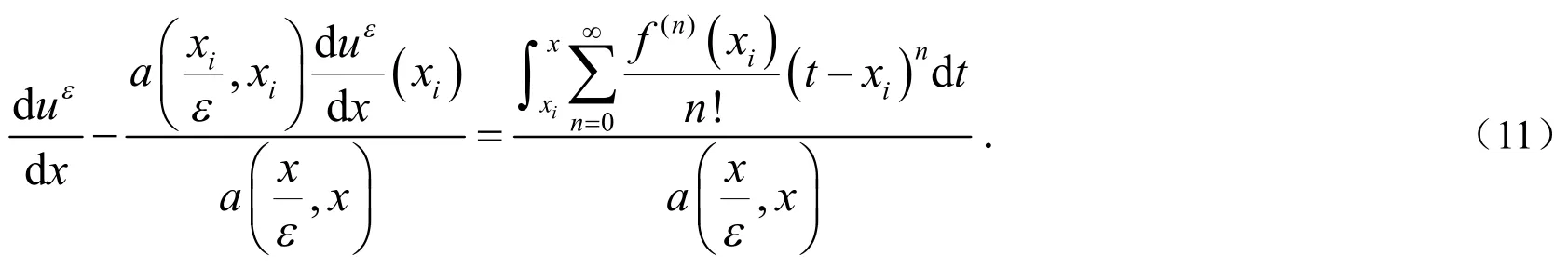
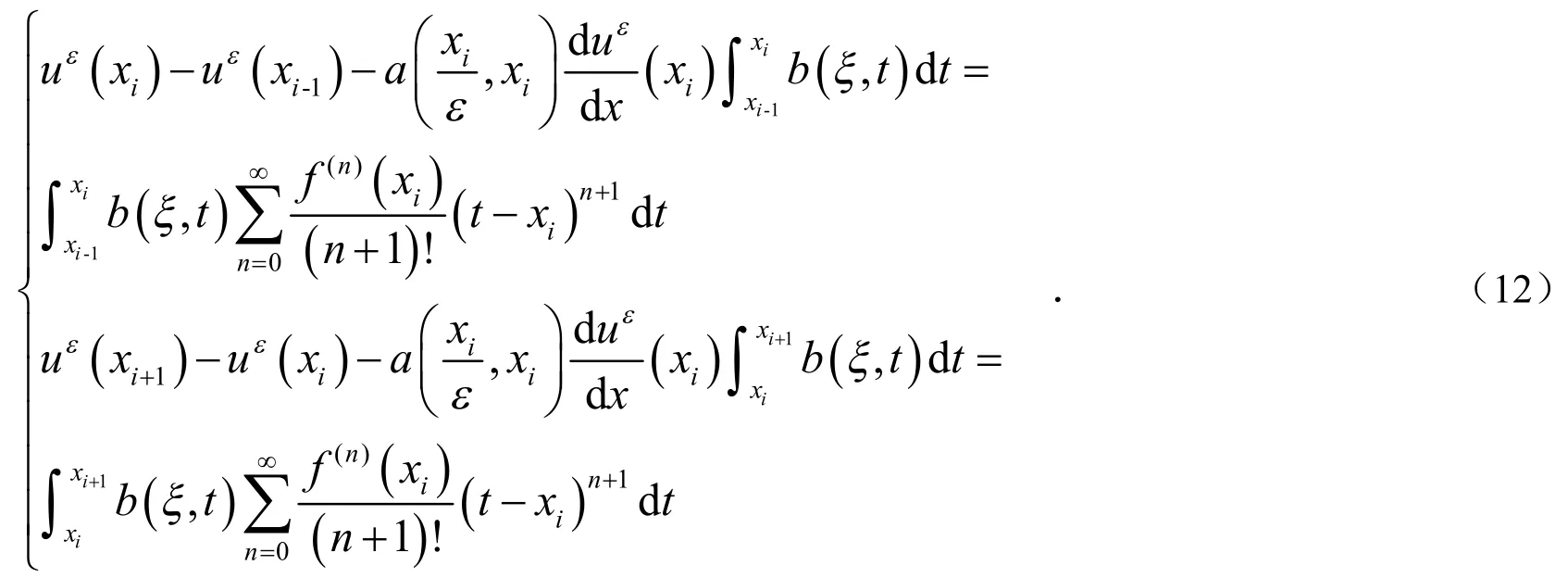
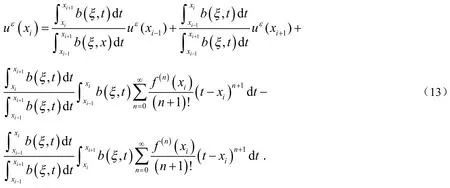
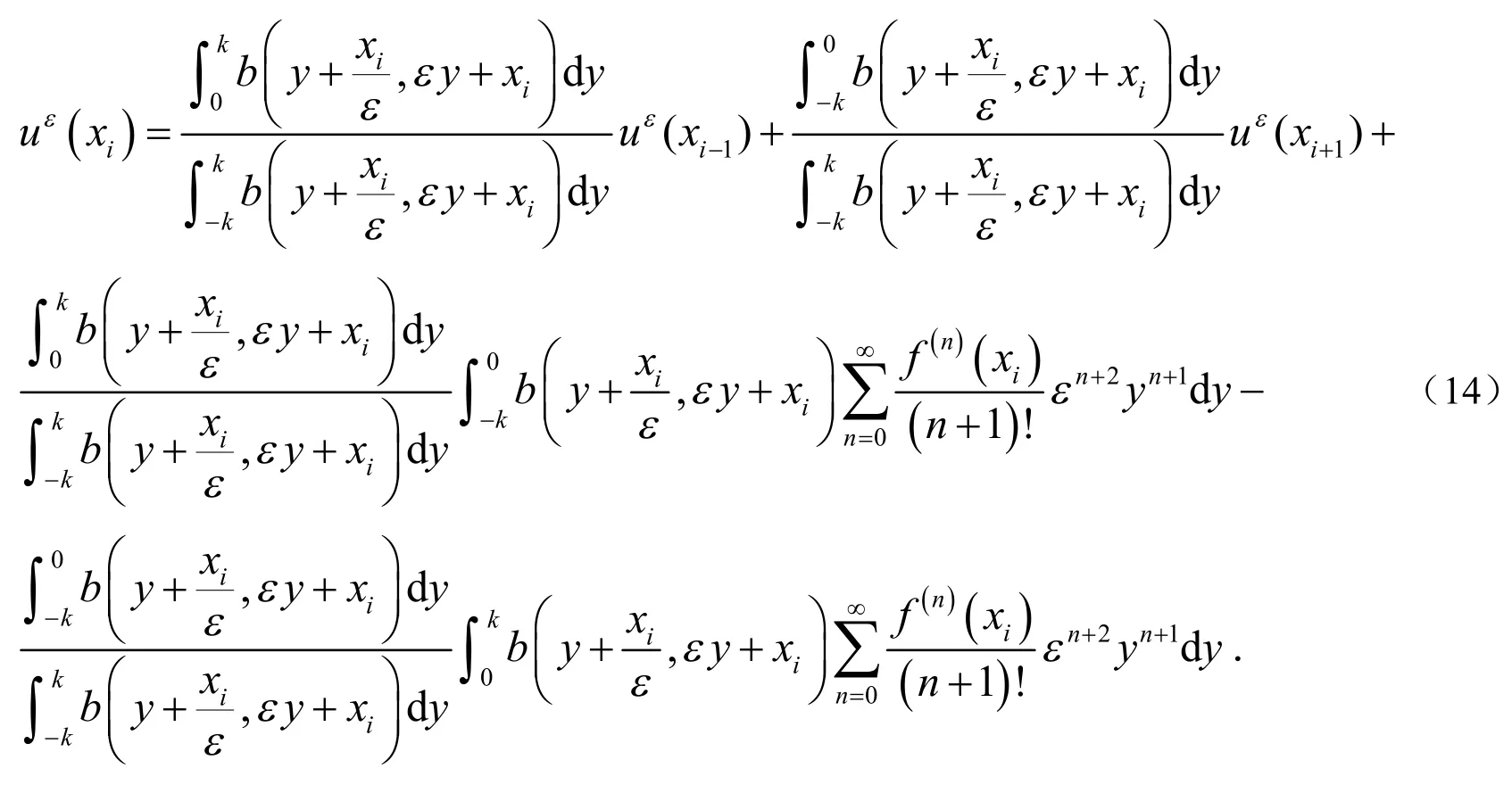
将(6)式带入(14)式得到:

对任意的j≥0,n≥0,令
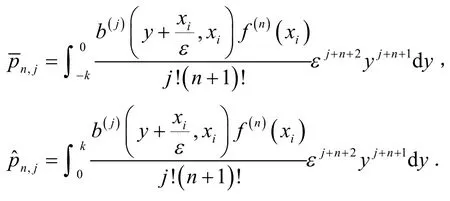
由(15)式得到:

引理2 当f≠0时,αi,βi,fi由上文定义有:

则有AU=F,显然A不可约且对角占优,故A可逆,U有唯一解.这样即可求得方程(1)在节点处的数值解.
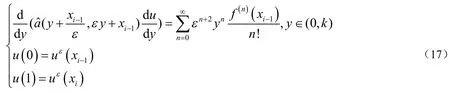
对(17)式在区间[0,y]上对积分得到:
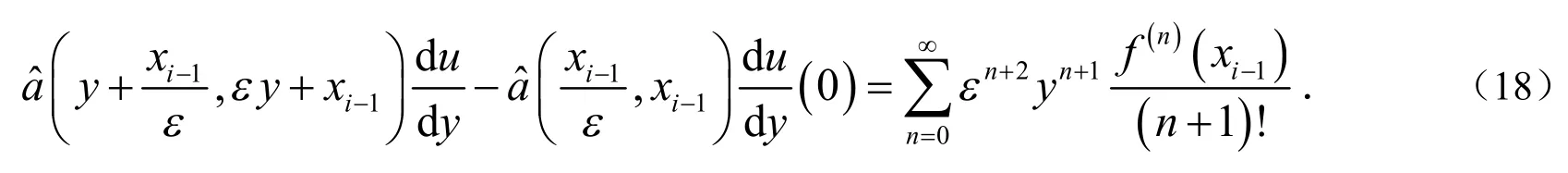
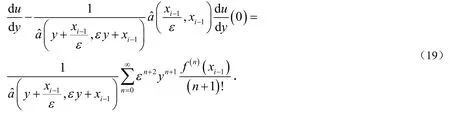
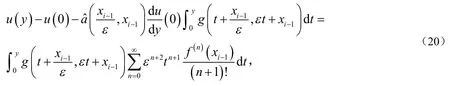
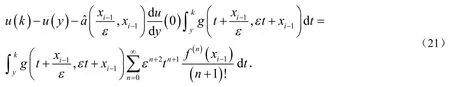
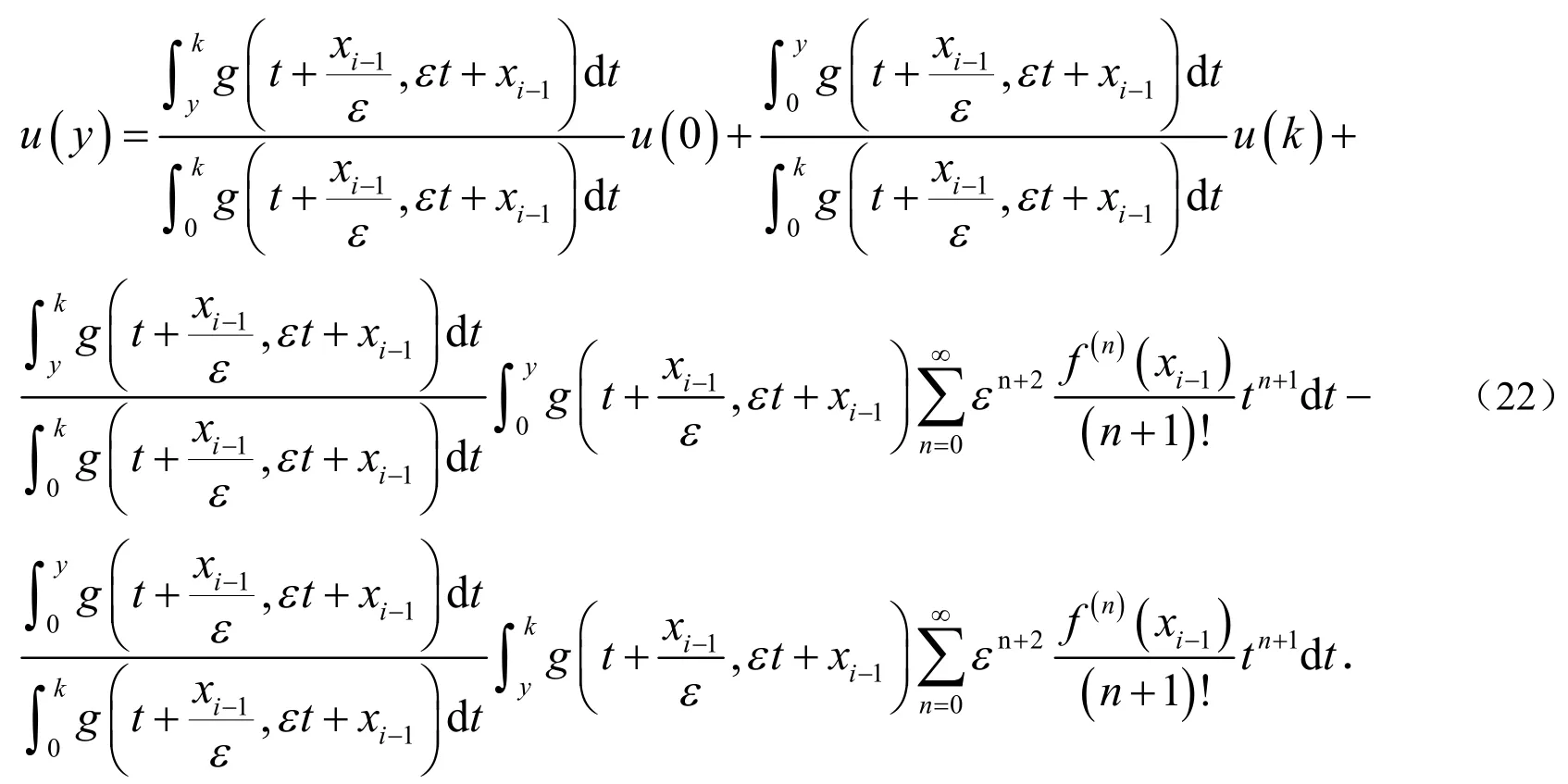
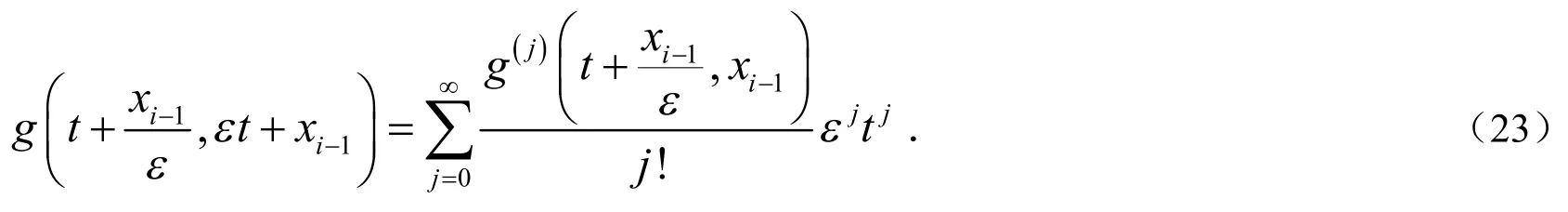
将(23)式带入(22)式得到:
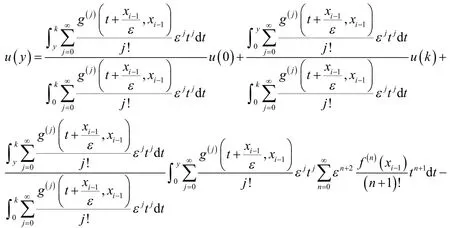
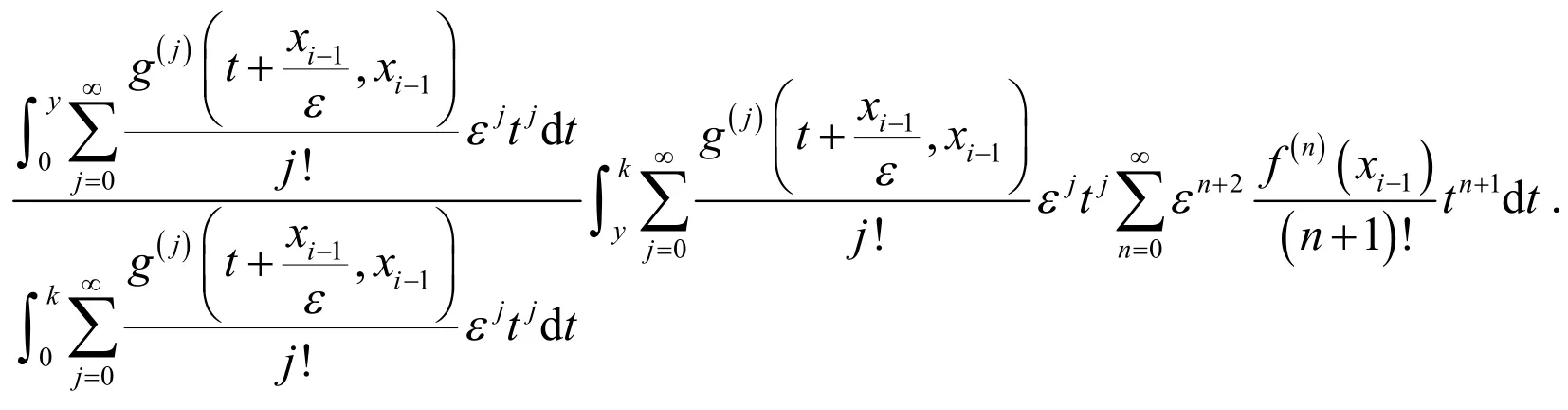
令
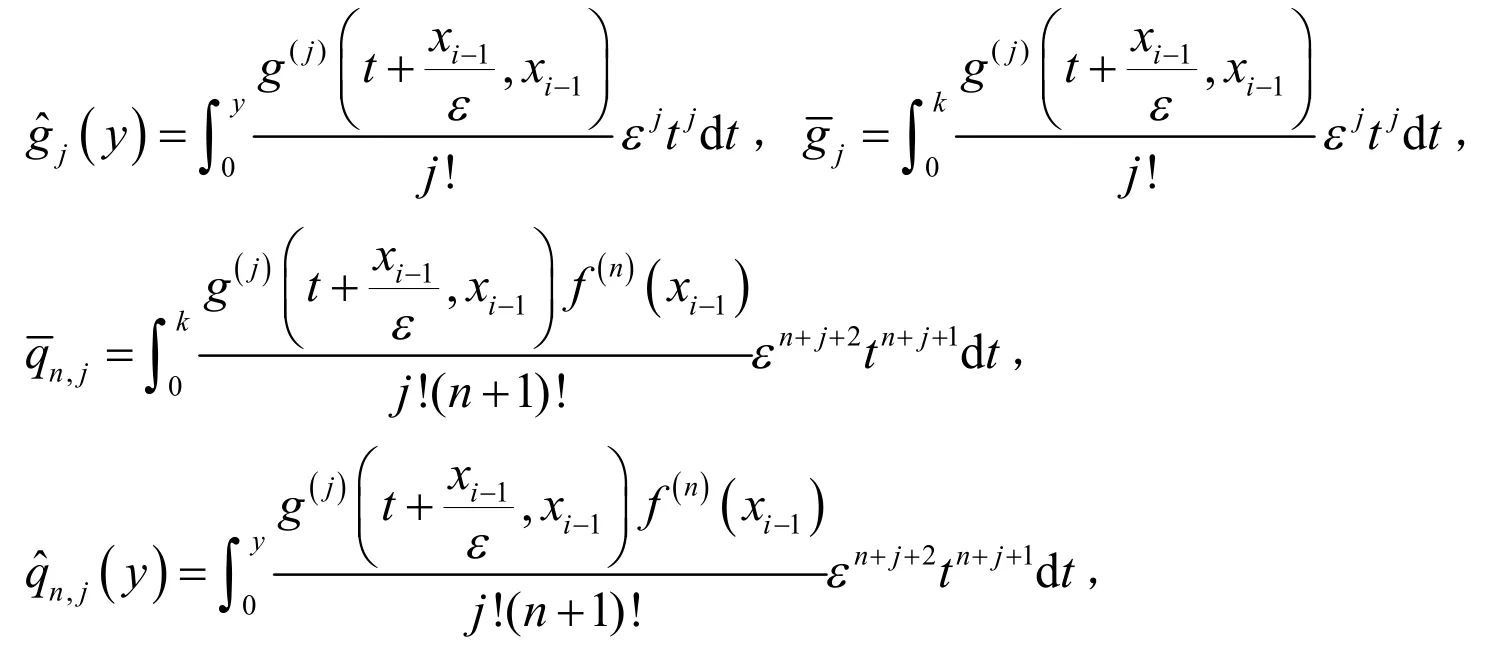
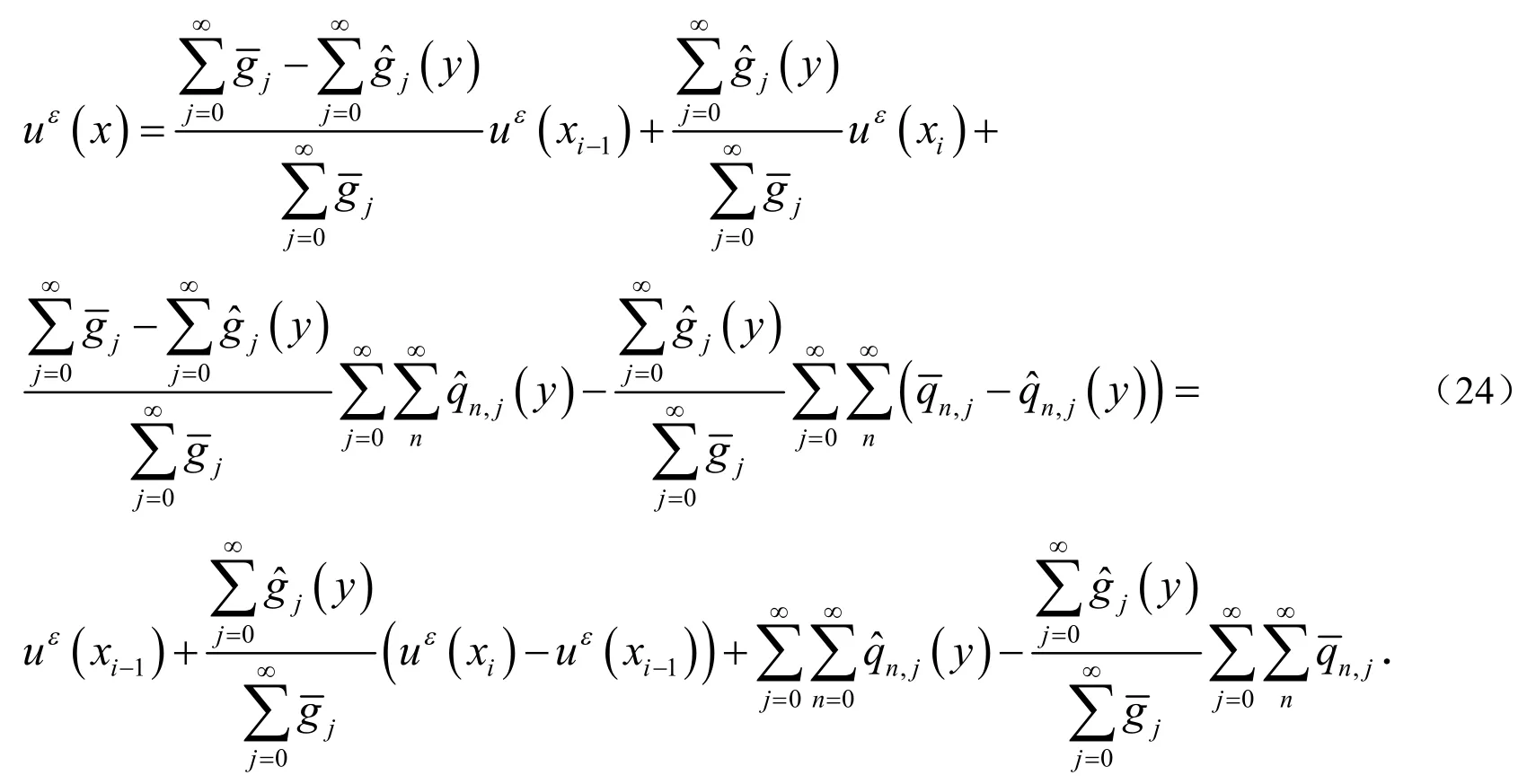
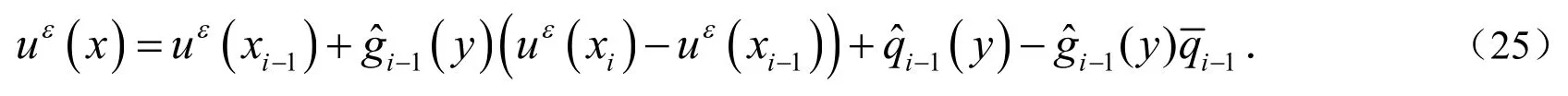
利用上述方法,可以得到方程(1)任意点的数值解.
2 数值算例
为验证算法正确性,给出如下算例结果.考虑方程:
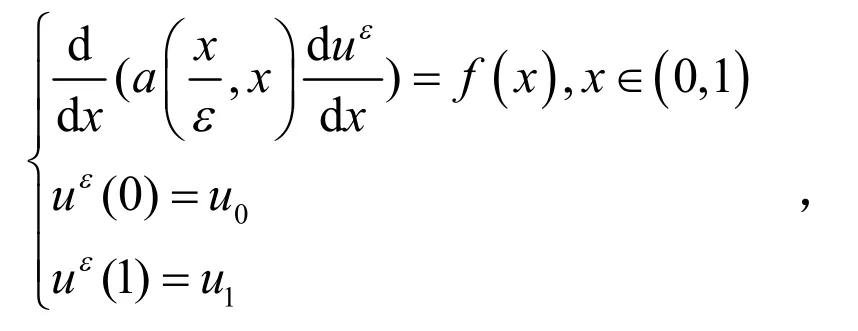

表1 本文算法与有限元法的最大绝对误差Table 1 Maximum Absolute Error of the Proposed Algorithm and the Finite Element Method
——抗爆炸减压弹性体

