图像
——在初中物理教学中的拓展
◎王珊婷
笔者根据在多年的教学经验,尤其在初中物理教学中教师不应该局限于课本,大胆的进行创新,结合数学中的几何线段关系、图像、一次函数的知识等使学生得到多方面的发展,数学知识就是解决物理问题的工具。应用它们可以得到事半功倍的意想不到的效果。也培养了学生学习物理的兴趣。现就下面一道有关追赶的问题进行展开讨论。
公路上,一辆汽车以72km/h的速度匀速行驶,它用30s追上了前方450m处的一辆匀速行驶的自行车,问这辆自行车的速度是( )
A、5m/s B、10m/s C、15m/s D、20m/s
分析:(把72km/h换算成20m/s)这是一种比较典型的追赶问题,笔者认为教师应该当做重点加以讲解、分析、并用多种方法进行拓展,让学生理解并能熟练的解决这类问题。
1、首先应该让学生搞清楚什么是相遇,以及相遇的条件,相遇的条件是两个物体同时到达同一位置。
2、利用题意做出汽车追赶自行车几何关系的示意图,根据几关系的何示意图解题具有直观性,学生容易理解和掌握。
4、理解速度——时间图像即v-t图像。在v-t图像中,图像和横、纵坐标围成的“面积”表示路程s。这里对面积打引号是借助数学是的面积表示位移,因为面积的单位是长度单位的平方。
解法一:利用题意做出汽车追赶自行车的几何线段关系的示意图,图(1)所示。A点表示汽车出发点的位置,B点表示自行车出发点的位置,C点表示汽车追上自行车的位置。即:两车相遇的位置。S0表示两车出发时相距的距离。根据几何线段关系的示意图可得下列方程组并推导得出自行车的速度。

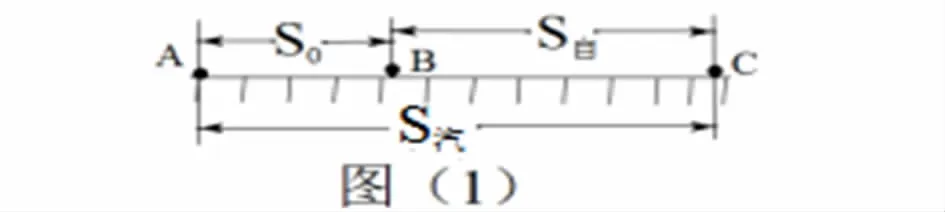
由以上三个方程组可得:V汽t=V自t+S0
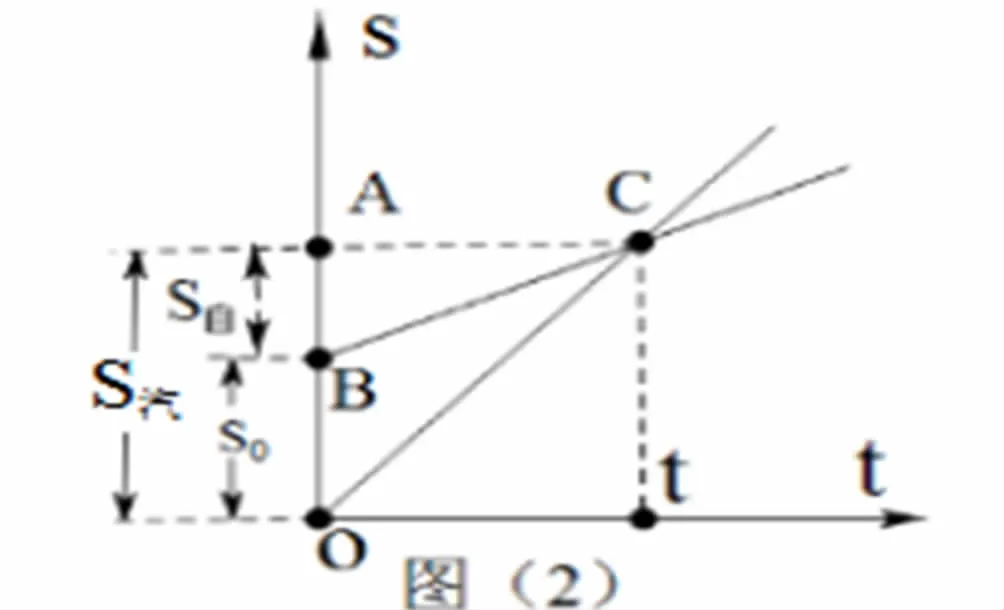
解法二:我们做出位移——时间图像,即s-t。图(2)所示,我们知道自行车在前面,后面的汽车和自行车同时运动还要追上前方的自行车,只能是汽车运动的速度必须大于前面运动的自行车的速度。根据位移——时间图像中的斜率表示速度可知,斜率大的(即陡度大的)表示速度大。所以图像中OC表示汽车运动的位移——时间图像,图像中BC表示自行车运动的位移——时间图像。图像中的OA段表示汽车在时间t内通过的路程,BA段表示自行车在时间t内通过的路程,OB段表示汽车和自行车在出发时相距的距离s0。同理可以得到解法一中的方程组可以解得:

解法三:我们做出速度——时间图像,即v-t。图(3)中图线1表示汽车运动的图像,图线2表示自行车运动的图像。图像中矩形ABCDD的面积则表示汽车追赶自行车之前的距离so。则有如下的方程:S0=(V汽-V自)t化简并代入数值可得:
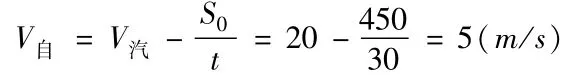

解法四:我们不妨根据图(2)所示引导学生写出汽车和自行车运动时的路程和时间的函数。
汽车运动的路程和时间的函数表达S汽=V汽t式为:
自行车运动的路程和时间的函数表达S自=V自t+S0式为:
我们从数学知识知道两条直线的斜率(即:自行车和汽车运动的速度不相等)不相等一定会相交于一点,这一点正好表示汽车追上了自行车。那么应该有:S汽=S自即有:V汽t=V自t+S0
代入有关的数据可得:20×30=V自×30+450从上式可以得出:V自=5(m/s)

