三通道转杯混色毛针织物Kubelka-Munk理论配色模型

徐亚亚，杨瑞华，邓茜茜，韩晨晨，薛 元，高卫东

(生态纺织教育部重点实验室(江南大学)，江苏 无锡 214122)

随着越来越多的人对服装面料高品质的追求，在纺织面料生产过程中对原料的要求越来越严格，原料的利用率越来越低。尤其是毛纺织品，由于其多用于制造高端产品，对纱线的要求非常高，因此在纱线纺制过程中会产生很多下脚料，基于转杯纺特殊的纺纱形式及原理，可以利用这些下脚料作为原料开发低支毛色纺纱线，以充分利用资源[1-2]。三通道转杯毛纺纱技术可以将转杯毛纺与色纺相结合，利用不同颜色的较短毛纤维生产低支毛混色纱。混色织物具有特殊多变的色彩风格，以满足消费者对服装面料时尚、个性化的需求。由于混色织物的颜色受所纺混色纱中纤维的颜色、种类、比重及织物结构等的影响，纤维的颜色及比重千变万化，使色纺织物具有丰富的种类和多变的颜色，因此开发混色毛织物的配色系统，可以大大减少实际生产过程中配色所需的时间及成本[3-4]。本文主要以Kubelka-Munk(简称K-M)双常数理论模型为基础，建立三通道转杯毛混色针织物的颜色模型，并分别用最小二乘法及相对值法求解K/S值，建立其对应的混色模型，并分别对相关织物的颜色及配方进行预测，分析预测效果，为计算机配色系统提供一定的理论基础。

1 实验部分

1.1 纺纱方法

本文实验利用三通道转杯毛纺细纱机独特的喂入机构及控制系统，将红、黄、蓝3种颜色的纯羊毛粗纱同时喂入组合式给棉罗拉，每个给棉罗拉都有独立的伺服电动机控制，根据所纺混色纱线的比例

及粗纱定量计算并设置每个给棉罗拉的线速度，控制每种颜色纤维的喂入量，喂入的各种颜色的纤维经过分梳辊分梳及转杯的高速运转，可使各种颜色的纤维混合均匀，经过加捻和牵伸纺制成特定工艺参数的混色纱线[5]。利用三通道转杯毛纺细纱机纺制混色纱，混色与成纱同步进行，不仅可以省去前纺工序中有色纤维的混合工序，缩短工艺流程，也可以随时更换纱线品种，简单易操作。多通道转杯纺纱机喂入部分示意图见图1。利用三通道转杯纺纺制的不同比例的纯羊毛混色配色样本见表1。

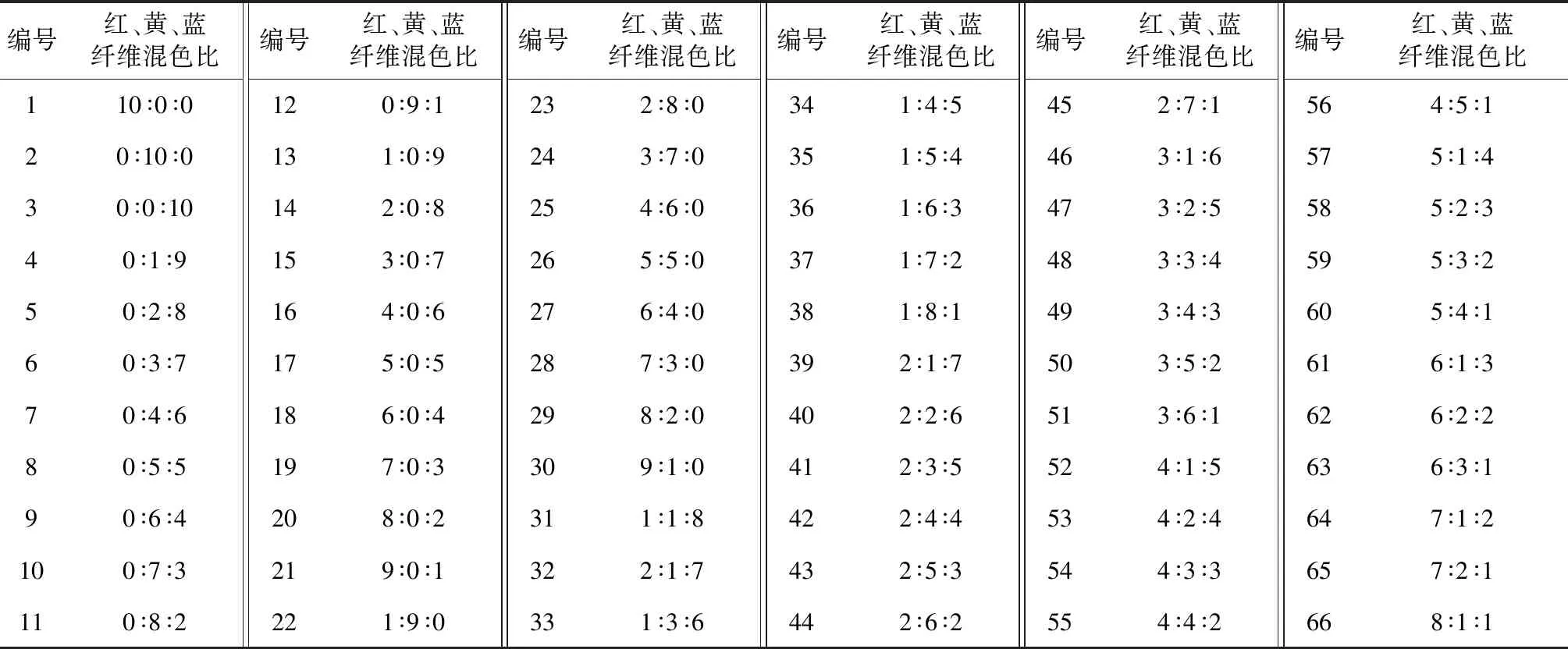
表1 混色纱配色样本

1.2 针织小样织造

将三通道转杯毛纺细纱机纺制的各组分不同比例的纱线，利用针织小圆机编织横密为9列/cm、纵密为12行/cm的纯羊毛针织平纹织物。织物色彩丰厚饱满，色彩柔和，其朦胧的立体视觉效果使布面颜色自然，富有层次感，满足消费者对时尚和个性化的追求。且毛纺原料与针织结构的结合，使面料手感柔软，富有弹性，有较高的服用性能。

1.3 颜色测量

为了测得不同纤维比例下各个布样的颜色，利用datacolor650分光光度仪测量样品在380～700 mm波长下的反射率。测量条件为D65标准光源、10°视场。为了能测量到布样最大面积，减少实验误差，实验测量取最大孔径30 mm。

2 K-M双常数理论模型建立及验证

Kubelka和Munk从完整辐射理论诱导出相对简单的理论，利用吸收系数K和散射系数S作为一个过渡参数简化了反射率和染料浓度之间的关系[6]，如式(1)所示：

(1)

式中：K/S值为不透明物体的吸收系数和散射系数比；R为样品在一定波长下的反射率。

由于不透物体的吸收系数K和散射系数S都具有加和性，对于混色织物来说，K/S值可表示为：

(2)

式中：i为第i种有色纤维；Ci(i=1，2，…，n)为混色样中各组分比例；Ki、Si分别为各单色纤维的K值和S值。

2.1 最小二乘法

最小二乘算法是通过建立线性独立方程组，利用系数矩阵来选择参数K和S，使得预测的因变量与实际值之间的差异最小[7]。将式(2) 展开并移项可得式(3)：

-C1K1-C2K2-C3K3+C1(K/S)S1+

C2(K/S)S2+C3(K/S)S3=0

(3)

由于混合物中混色纤维的比例是已知常量，混色纤维的K/S值可以通过反射率计算得到，因此将线性方程组的系数常量表示如下：

Am,1=-C1

(4)

Am,4=C1(K/S)

(5)

Am,2=-C2Am,5=C2(K/S)

(6)

Am,3=-C3

(7)

Am,6=C3(K/S)

(8)

由于线性方程组的右侧为零向量，会使得解向量为零向量，为了使约束方程组避免这一现象产生，将系数矩阵B及右侧矩阵Y的最后添加附加行，由此可得：

(9)

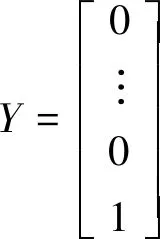
(10)

(11)

因此线性方程组可用矩阵表示为：

Y=BX

(12)

通过最小二乘法的矩阵运算求解出特定波长下3种有色纤维的K、S值。

X=(BTB)-1BTY

(13)

2.2 相对值法

相对值法是由Burlone提出的用于计算9种有色锦纶纤维的K值和S值。该方法是将多种有色纤维分别与其中一种纤维混合，并假定这种纤维的吸收系数与散射系数，得出其他有色纤维的相对吸收系数及散射系数[8]。当2种纤维混色时，式(2)可以表示为：

(14)

假设其中一种纤维的S1=1，则

K1=(K/S)1S1=(K/S)1

(15)

式中 (K/S)1为该单色纤维测得的K/S值。

已知另一种纤维K、S值有以下关系：

(16)

式中 (K/S)2为单色纤维的吸收系数和散射系数比。

联立式(14)、(15)、(16)，可得该纤维的散射系数为：

(17)

则该纤维的吸收系数为：

K2=(K/S)2S2

(18)

利用相对值法对每种有色纤维的K/S值进行求解，并取其平均值，使求得的解更为精确。

2.3 配方预测

用以上2种方法求得的K、S值可以分别建立基于K-M理论关于三通道转杯毛色纺纱的配色模型，然后可以根据模型计算混色织物中各颜色羊毛纤维的比例。本文利用最小二乘法求解纤维的混色比例，使预测比例与实际比例之间的差异最小，并计算其他平均比例误差[9-10]。

2.4 色差计算

根据以上配色模型，利用式(19)计算得到预测反射率，可以计算得到预测样本与实际样本之间的色差，本文利用CMC(l:c)色差式对样本色差进行计算，如式(20)所示。

R=1+K/S-[(K/S)2+2×K/S]1/2

(19)

(20)

式中：ΔECMC为样本色差；ΔL、ΔC、ΔH分别为明度差、饱和度差和色相差；SL、SC、SH分别为ΔL、ΔC、ΔH的加权系数；l=2，c=1。

3 结果分析

为了分别利用最小二乘法及相对值法建立关于三通道转杯毛针织混色织物的K-M双常数配色模型，本文实验制备的样本中，4～30号样本用于最小二乘法求解吸收系数K及散射系数S，1～21号样本用于相对值法求解K、S值。利用最小二乘法及相对值法求解的K、S值见图2、3。

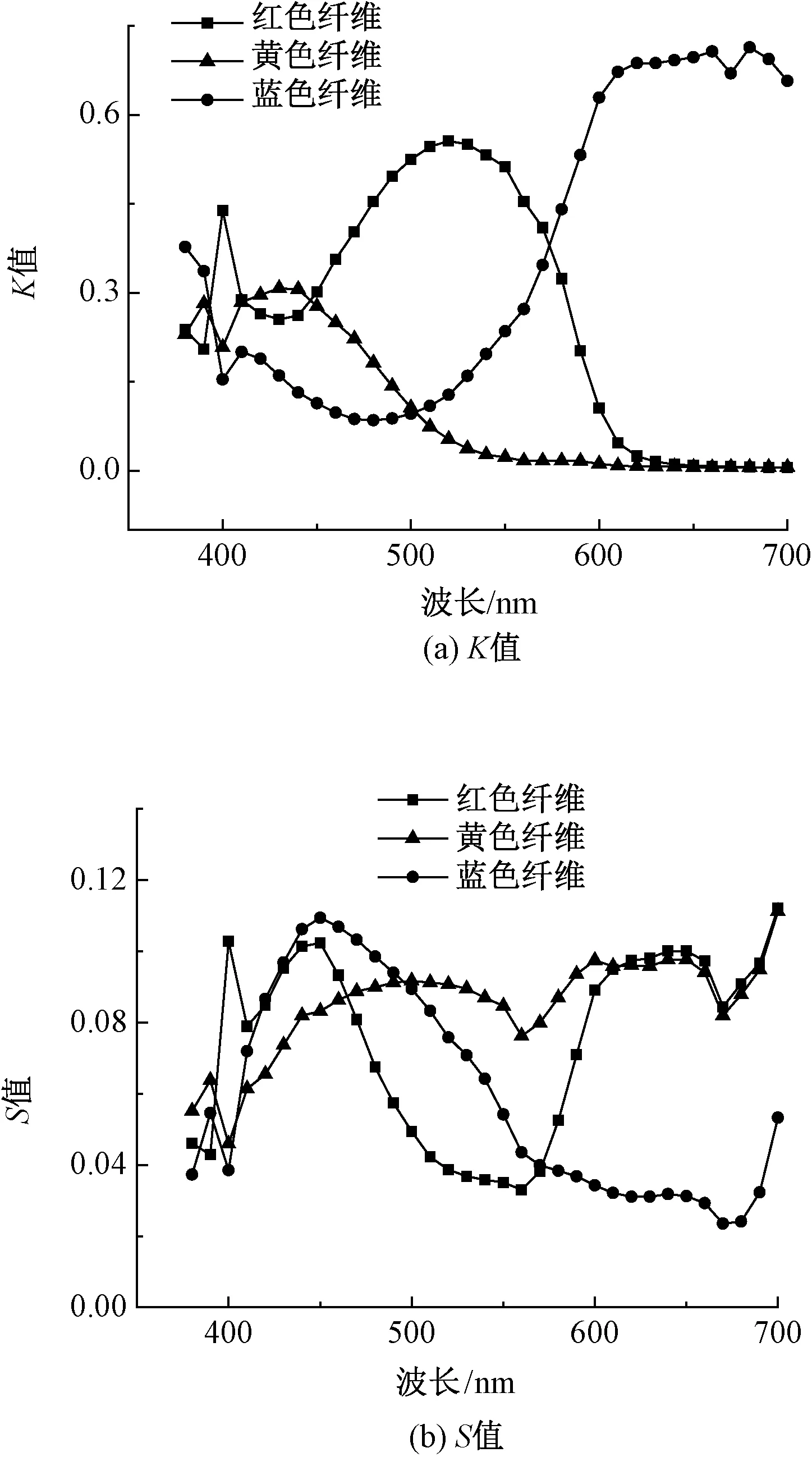
图2 最小二乘法求解K、S值

根据以上计算得到的单色纤维的K、S值及各颜色纤维的比例，根据式(2)可以得到一定比例下混色织物的K/S值，并利用式(19)求得不同波长下混色织物的反射率。将4～66号的所有样本分为2组分(含2种颜色纤维，下同)织物及3组分织物用于配方预测及色差计算,其中2组分样本共27个，3组分样本共36个。利用最小二乘法及相对值法建立K-M理论模型的配色结果见表2。

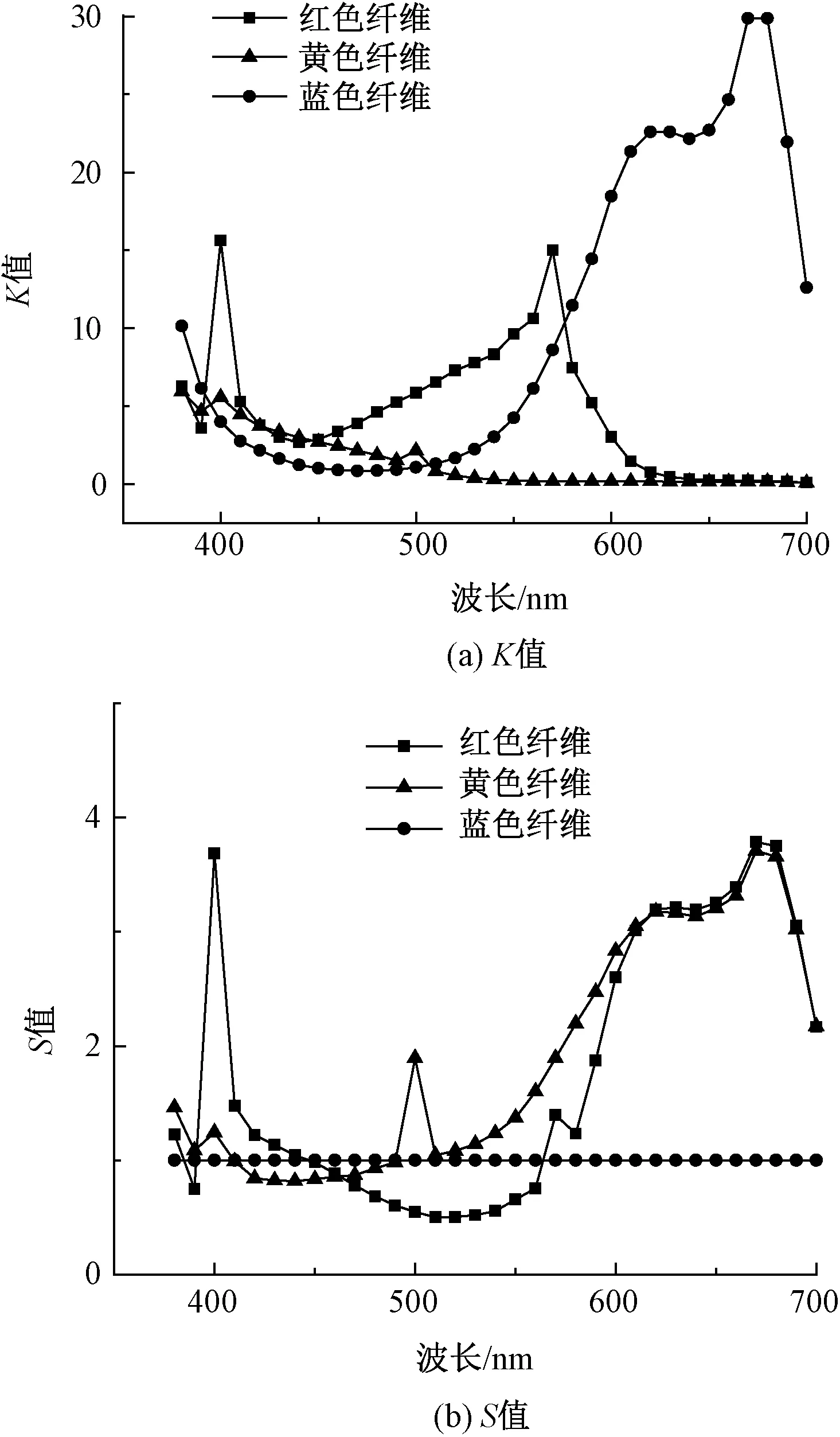
图3 相对值法求解K、S值

表2 K-M理论模型的配色结果

由表2可知，利用最小二乘法建立的配色模型，无论是2组分还是3组分样本，其色差均值均小于1；3组分样本色差小于1.5的样本合格率为100%，2组分样本中只有1个样本的色差大于1.5；预测的2组分及3组分配方的比例误差均值分别为0.80%和1.99%，预测结果较好。

利用相对值法预测样本颜色，其2组分样本的色差均值为0.306；当容差范围为1时，样本合格率达到100%。3组分样本的色差均值为0.763，色差小于1.5时的样本合格率相比其他较低。2组分及3组分预测配方的平均比例误差分别为1.56%和2.87%。

由以上分析可知，对于2组分混色织物，相对值法的颜色预测结果比最小二乘法的预测结果要好，但其配方预测的结果没有最小二乘法的预测结果好；对于3组分混色织物，利用最小二乘法预测的颜色及配方均比相对值法预测的结果要好；3组分样本织物中，有几个样本无论是用最小二乘法还是相对值法，其求得的样本色差相对较大，这可能是由于样本在制作过程中造成的人为误差或测量过程中造成的测量误差引起的。

4 结束语

本文针对三通道转杯纯羊毛针织混色织物的配色规律，分别利用相对值法和最小二乘法求解吸收系数K和散射系数S，以建立三通道转杯纯羊毛针织混色织物的配色模型，并对2组分织物及3组分织物进行模型验证，结果显示，2种方法预测的色差均值均在1个色差值左右，平均比例误差在3%以下。最小二乘法对3组分织物的预测结果较好，而相对值法对2组分织物的预测结果较好。

利用较短羊毛纤维在三通道转杯毛纺细纱机上生产纯羊毛低支混色纱线，不仅可以使原料得到充分的利用，增加企业的生产效益，而且可以任意混配颜色，缩短生产流程，符合市场的发展方向。本文的研究内容可以为三通道转杯混色毛纺针织物的混色配色研究提供理论参考。