基于麦克纳姆轮的全向AGV移动平台控制方法研究

房殿军，卢彦廷，申加宁

（1.同济大学 中德学院，上海 201804；2.中德智能技术博士研究院，山东 青岛 266500）

1 引言

本文研究对象为基于麦克纳姆轮的全向AGV（Automated Guided Vehicle，无人搬运小车）移动平台，属于轮式移动机器人。麦克纳姆轮为瑞典麦克纳姆公司专利发明的全方位车轮，由于麦克纳姆轮上斜柱辊子结构的受力特点，使得搭载该轮的AGV系统只需通过控制每个麦克纳姆轮的正向或反向转动关系，便可以实现三个自由度的全方向运动控制[1]。

传统PID控制往往采用Ziegler-Nichols整定法得到PID参数，确定后也不再进行调整。因此传统PID渐渐无法适应更加复杂的控制系统和满足智能算法对底层控制更高的要求。引入模糊控制与PID控制结合，可通过不断检测系统反馈的误差e与误差的变化ec，根据模糊推理规则，实时在线调整PID控制器参数，达到优化系统控制品质的目的。遗传算法具有快速全局寻优的特点，能根据系统的不同要求对经典模糊控制规则进行优化。利用Vague集相似度量理论，可简单敏捷地匹配实际反馈误差与离线优化后的模糊控制规则，通过查表的形式快速整定PID参数，比单独使用模糊PID更加简单迅速，也更适用于实际工程项目之中。

2 麦克纳姆轮全向AGV移动平台运动学模型

麦克纳姆轮（Macanum Wheel或称Ilon Wheel）是由瑞典工程师Bengt Ilon于1973年发明，它由一组围绕轮体对称放置的若干个全等辊子组成（如图1(a)所示）[2]。每个辊子的表面都是基于母线旋转形成的表面，其轴b与轮轴a之间存在一定角度，而通常a和b之间的角度δ选择为+45°或-45°。一般基于麦克纳姆轮的移动AGV会装有四个类似结构的轮子，每一个麦克纳姆轮都由一个独立的电机进行驱动，该电机提供的扭矩经过麦克纳姆轮传递至地面后能够为车辆提供在平地上进行全向运动所需的三个自由度。

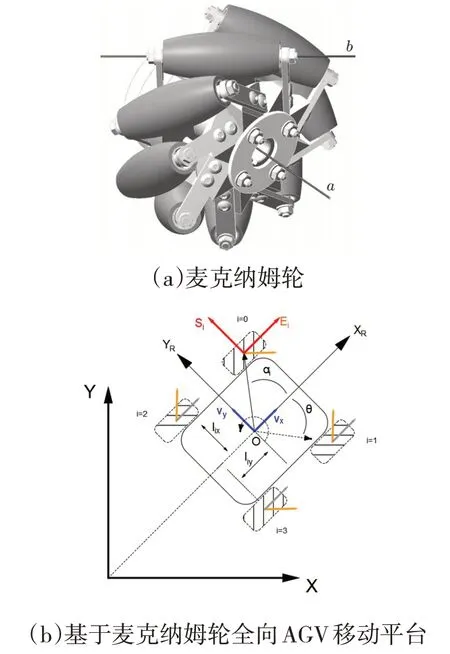
图1 基于麦克纳姆轮全向AGV模型

如图1（b）所示，基于该全向AGV建模参数如下：

X,G,Y:惯性坐标系；

x,y,θ:AGV位置坐标以及AGV转动角度（XR正方向与惯性坐标系x轴的夹角）；

XROYR:AGV坐标系，AGV中心的运动与惯性坐标系相关；

SiPiEi:第i个麦克纳姆轮轮心Pi的坐标系；

OPi:AGV中心与轮心的矢量距离；

lix,liy:lix为两前轮轮心距离的1/2，liy为前轮与后轮轮心距离的1/2；

αi:OPi和XR之间的夹角；

βi：Si和XR之间的夹角；

γi：νir和Ei之间的夹角；

ωi[rad/s]:轮角速度；

νi[m/s]:根据轮角速度换算所得速度矢量；

νX,νY[m/s]:AGV速度矢量；

ωZ[rad/s]:AGV转向角速度。

假设麦克纳姆轮在地面上运动时没有打滑，且每个辊子中独立的变量νi和ωi与AGV系统的角速度和线速度之间存在关系，系统反向运动方程见式（1）。

表1中记录了AGV系统的各个参数取值，进而系统反向运动方程可化简推导得出式（2）。

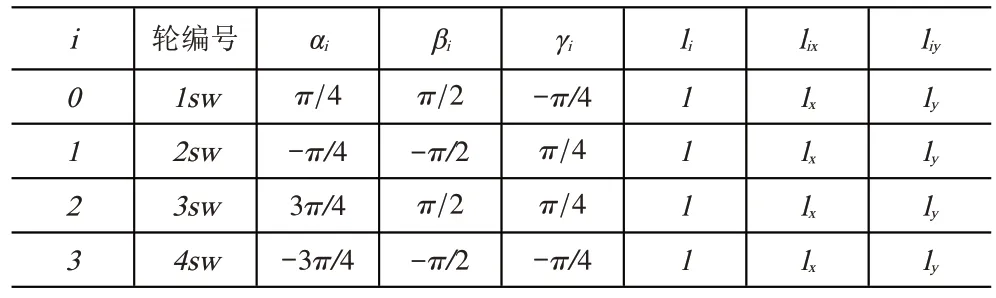
表1 全向AGV系统参数

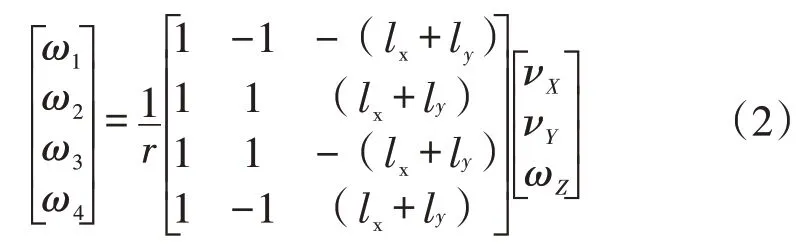
而系统的正向运动方程见式（3）。

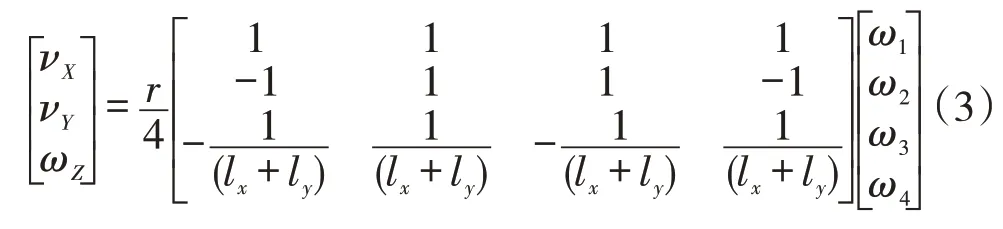
3 基于麦克纳姆轮的全向AGV移动平台控制方法

3.1 遗传算法优化模糊控制规则

遗传算法对模糊推理规则优化方法设计采用二维控制器结构,输入量为误差e及误差变化率Δe,输出量为ΔKP、ΔKI或ΔKD，通过PID控制器获得控制量u并作用于被控对象。e、Δe、ΔKP、ΔKI、ΔKD均可被7个语言变量值之一表示:NL、NM、NS、ZO、PS、PM、PL，在基因编码中分别对应二进制数001，010，011，100，101，110，111。若模糊控制规则为“if E is NL and EC is NL then U is PL”,则模糊推理规则由二进制编码可表示为001001111。

算法中的适应度函数选择ITAE时间乘误差绝对值积分性能指标评价，许多文献研究均认为这是兼具工程实用性和选择性以及单参量最佳控制和自适应控制中经典的性能指标之一。

ITAE评估指标值越小，代表控制系统性能越好,为了便于计算机编程即时计算该指标，需要将该方程改为离散化的表达方式：

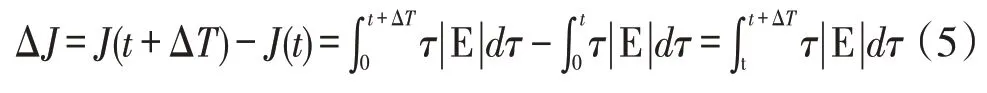
遗传算法优化模糊推理规则流程架构如图2所示。初始群体由Ni组个体组成，Ni=30。若交叉率为Pc可新创建Nc种个体，并且根据突变率Pm新生成Nm种个体。总共可获得由N（N=Ni+Nc+Nm）种个体组成的群体P用于模型模拟。一般遗传算法中，选择Pc=0.8，Pm=0.05。

基于遗传算法优化后的Kp、KI、KD的模糊推理规则见表2。

模糊推理结果为输出论域上的一个模糊集，通过加权平均法，又称为重心法（Centroid），可解析得到论域上的精确值，见式（6）。解析结果见表3。

3.2 Vague集相似度量理论

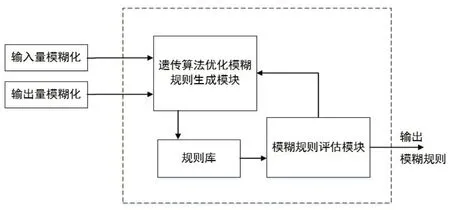
图2 模糊控制规则优化流程

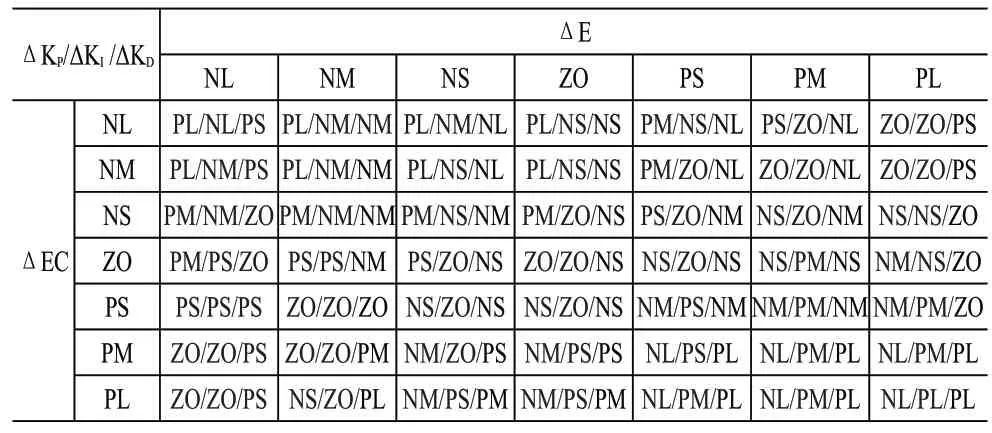
表2 优化后ΔKP、ΔKI、ΔKD推理规则表

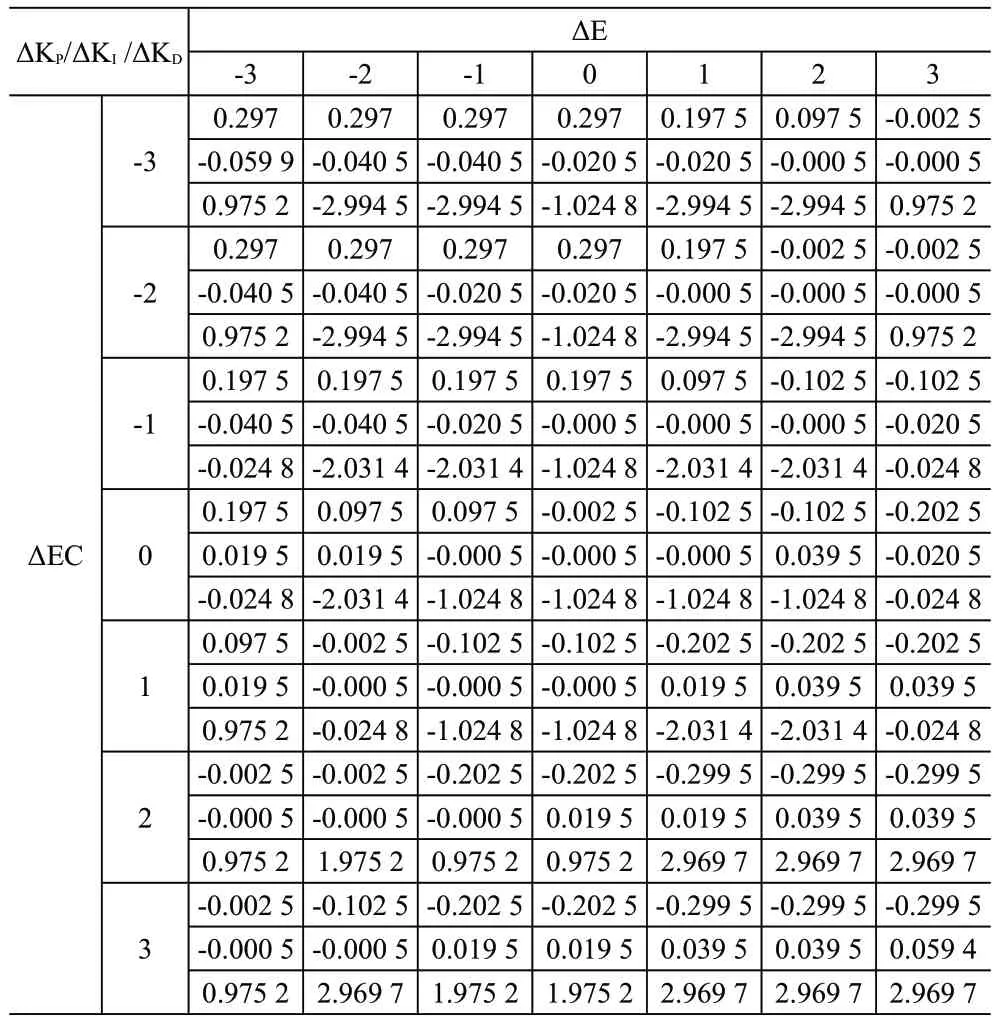
表3 优化推理规则解模糊表

Gau与Buehrer在1993年发表于IEEE中论文提出了Vague集理论，是在模糊理论的基础上，进一步提出真隶属度与假隶属度函数以及不确定度等概念，有助于更准确地描述问题对象间的模糊性质以及分析由此产生的模糊信息[3]。

假设论域U是离散且有Vague集A，A可表示为：

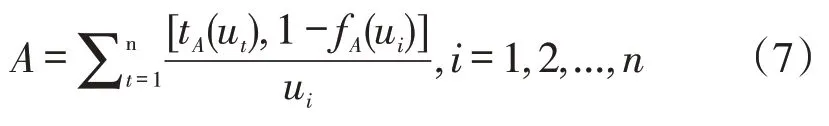
Vague集A中有两个数x与y，则可表示为x=[tx,1-fx]与y=[ty,1-fy],且tx,y+fx,y∈[0,1]，并有关系：

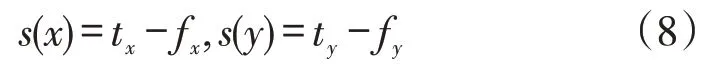
x和y之间的相似程度由函数M进行计算：

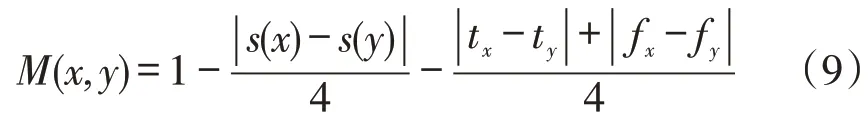
假设论域U中还有Vague集B，则两Vague集之间的相似程度用函数T进行计算：

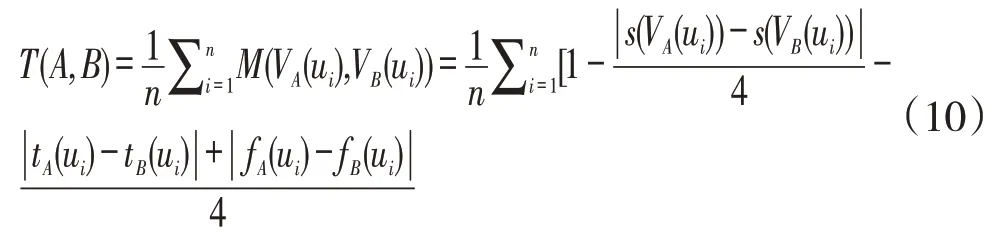
从上文可知，模糊控制规则P的推理方法如下：

P1 if P11 and P12 and,…,and P1m then Q1

P2 if P21 and P22 and,…,and P2m then Q2

P3 if P31 and P32 and,…,and P3m then Q3

……

Pn if Pn1 and Pn2 and,…,and Pnm then Qn

事实R: if P1 and P2 and,…,and Pm

结论Q： Q

事实R与Pi匹配程度用函数T表示，T（R，Pi）表示如下：

计算出匹配度最高的Pi记为Pmax。

则结论为：Q=T(R,Pmax)×Qmax

使用Vague集相似度量理论时，在遗传算法优化的模糊控制规则表基础上，输入实时采集反馈的ΔE、ΔEC值后，通过计算实际反馈所得误差与误差变化量和每一条控制规则的匹配度，并选用匹配度最高的控制规则（算例从略）。由已知的AGV运动模型与实际选用电机参数，可得出前进速度vx、横移速度vy与AGV角速度ωZ控制系统的传递函数。其中，用于参照比对的传统PID控制参数取值见表4。

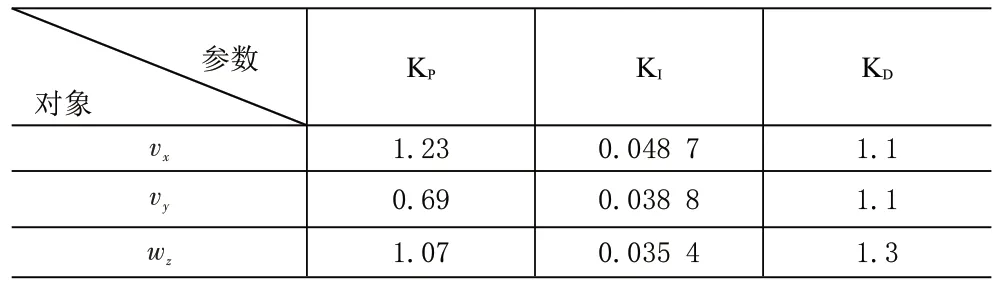
表4 传统PID控制参数

前进速度vx传递函数见式（12），仿真结果如图3所示。

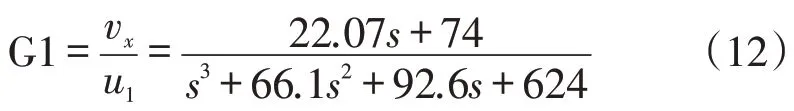
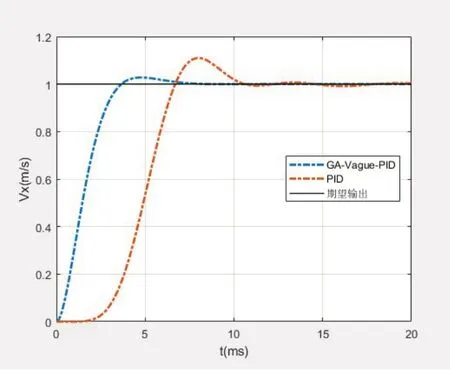
图3 速度vx仿真结果

横移速度vy传递函数见式（13），仿真结果如图4所示。

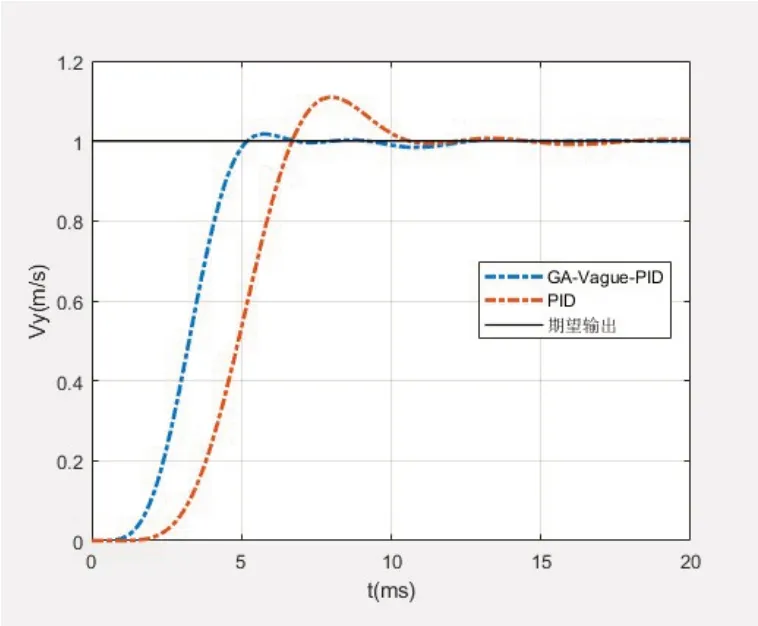
图4 速度vy仿真结果

AGV角速度ωZ传递函数见式（14），仿真结果如图5所示。

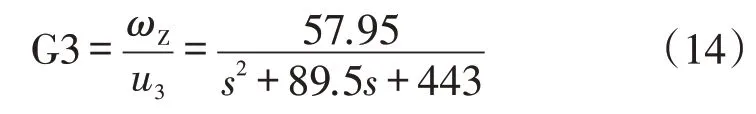
4 结语

通过上述研究可以得出，引入了遗传算法与Vague集相似度量理论在线调整PID参数的控制方法，能使目标AGV系统的前进速度控制、横移速度控制以及系统转动角速度控制超调量分别减少74.7%、84.3%与61.1%，调整时间分别缩短6.27ms、4.65ms与4.36ms，提高了该AGV系统的稳定性以及机动性。结果表明，该方法在基于麦克纳姆轮的全向AGV控制系统中，相比于传统的PID控制方法，有更好的控制性能与更迅捷的响应速度。

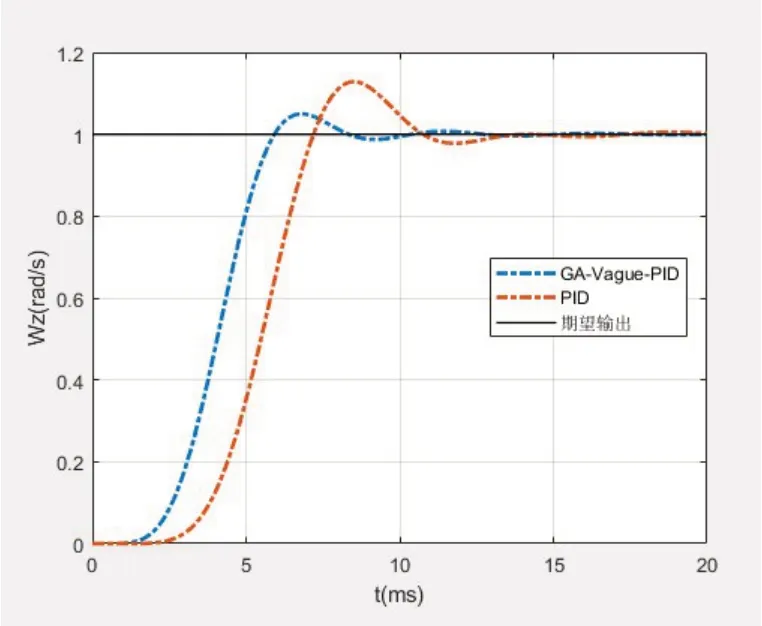
图5 系统角速度wz仿真结果