矿井环境探测机器人的越障能力分析

杨忠炯，李坤霖，周立强

（1.中南大学 机电工程学院，长沙 410083；2.中南大学 高性能复杂制造国家重点实验室，长沙 410083）

0 引言

地下矿井有着十分复杂的地形，且偶有事故发生。为了避免工人在状况不明的区域发生事故，可以利用机器人先行进入进行探测，以降低事故发生的风险。履带机器人因其特有的结构以及环境适应能力，可以应用于矿井的环境探测。履带机器人在矿井行走时面临的是各种各校的非结构环境。信建国等对非结构化环境进行了分析并总结出斜坡、沟道、台阶等3种典型障碍地形[1]，并提出非结构化环境是这3种典型地形的任意组合。美国在阿富汗战场大量投入的Packbot机器人，采用了2条主履带和2条摆臂履带的双摆臂形式，具有较强的越障能力。中国矿业大学救援技术与装备研究所于2005年开发了国内首台用于煤矿环境探测以及煤矿灾难搜救的机器人CUMT-I型，该机器人携带多种传感器，可以探测到诸多有害气体、粉尘浓度以及其他有害物质。已经有不少文献对履带机器人的越障机理及越障能力进行了研究。文献[2]分析了四履带双摆臂机器人的越障机理及越障能力，文献[3]研究了一种关节式履带机器人攀爬楼梯的动态稳定性问题。文献[4]提出了一种具有被动摆臂的履带机器人，并将其越障能力与其他类型的履带机器人做了对比。过往的研究大多集中在机器人分别面临斜坡、沟道、台阶时的越障机理和越障能力，并未考虑其中某两种或三种地形组合在一起时的情形。

地下矿山的环境复杂多变，研究履带机器人在面临复杂地形时的越障机理及越障能力，可以对机器人在越障时的姿态、摆臂动作进行提前规划，还可以预知所面临的地形能否顺利通过。本文从运动学的角度，在单独研究双摆臂履带机器人面临台阶、沟道时的越障机理和越障能力的基础上，研究了台阶与沟道组合时，机器人的越障机理与越障能力。为机器人在面临复杂地形时通过性提供理论依据。

1 探测机器人的总体设计

矿井环境探测机器人结构特点如图所示。因为地下矿井的地形复杂多变，所以机器人要有较强的越障能力。因此，在传统的双履带机器人基础上，加装两条摆臂履带，在遇到一般履带机器人难以通过的地形时，可以依靠摆臂对机器人的撑起实施越障。摆臂的存在可以使机器人的质心前移，对于越障能力有一定的提升。机器人采用两个无刷直流电机后驱，再单独采用两电机实现摆臂的独立摆动。摆臂既可以同步运动也可以独立运动。机器人整体采用模块化设计，可分为箱体模块、主履带模块、摆臂模块。其中，箱体模块将传统的整体式车厢改成三个独立的箱体，将驱动装置、摆动装置以及电气元件分开，避免互相干扰；而且在加工上也存在便利。

2 矿井环境探测机器人的越障机理

矿井的地形环境十分复杂，为了便于分析与表述，通常将障碍地形简化为斜坡、台阶、连续台阶、凸台、沟道等具有典型特征的地形[1]。

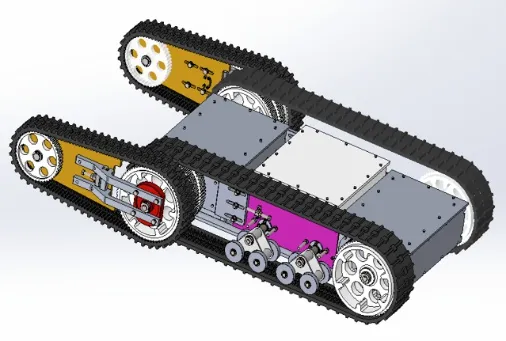
图1 探测机器人外形结构示意图

在地下矿井中的复杂障碍大多为爆炸或开采后留下的乱石堆，为了便于分析，可以将乱石堆等复杂地形看成台阶与沟道的组合地形。台阶的关键几何特征是其高度，其关键边界线为台阶外角线，如图2(a)所示。沟道的关键几何特征是其宽度，其关键边界线为沟道两侧边界线，如图2(b)所示。

从质心运动学的角度，履带机器人的成功越障是指机器人利用传动装置驱动履带前进，同时在自身的辅助装置，如摆臂、支腿等机构的帮助下，使机器人的整体质心越过障碍。越过之后机器人能继续前行，不会被障碍卡住、不发生翻转[2]。

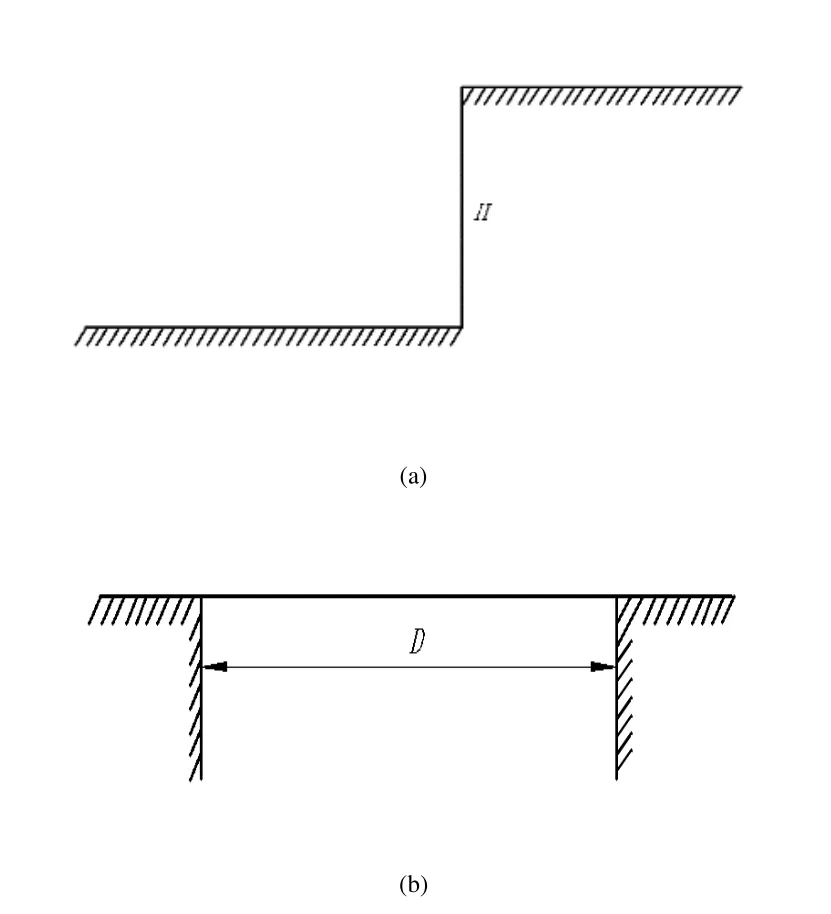
图2 台阶与沟道简化图

3 探测机器人的越障能力分析

3.1 探测机器人的质心分布[4]

为了研究加装了摆臂的履带机器人质心分布特点，可简化其外形，建立如图3所示的平面模型。将机器人分成主履带部分和摆臂部分。建立以机器人后履带轮圆心为原点的平面坐标系xO1y，令机两履带轮圆心O1O2的间距为l0，主履带部分质量为m1，质心坐标G1（l1，h1），两摆臂总质量m2，质心为G2，处于摆臂中心线O2O3上，且距离前履带轮圆心O2的长度为l2，摆臂轮与主履带前轮的圆心O2、O3的间距为l3，摆臂的摆角为θ，设主履带部分两个履带轮半径为R，摆臂履带前轮半径为r，则其整体质心坐标G0（x，y）为：

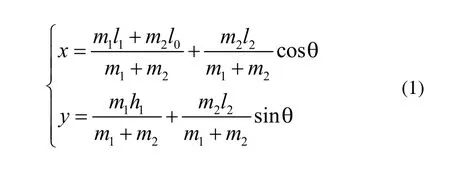
探测机器人的质心满足以下关系：

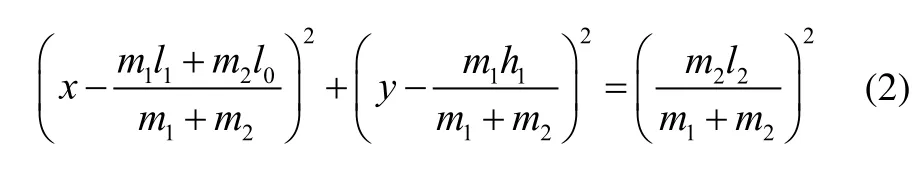
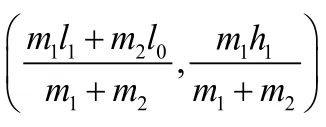
机器人的主要参数为：R=130mm，r=95mm，l0=650mm，l2=185mm，l3=380mm，m1=50kg，m2=10kg；通过三维软件可以求出主体部分的质心坐标为：l1=420mm，h1=80mm。

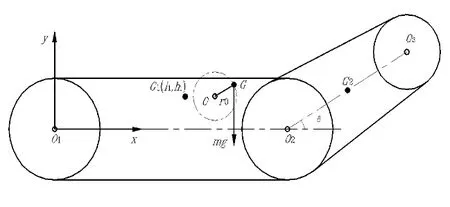
图3 机器人的质心轨迹

3.2 机器人攀爬台阶

机器人面对台阶的越障过程如图4所示，机器人凭借自身驱动力驱使履带向前运动，在快面临台阶时，摆臂前端搭接在台阶外角线上，随后依靠摆臂驱动电机驱动摆臂向下摆动，将车身前半部分抬离地面。机器人继续向前运动，车身仰角变大，质心位置也随之前进和上升；当质心超过台阶的外角线时，机器人后轮会在前半部分重力的作用下脱离地面，机器人整体随之向下翻转至水平线，并保持与水平行走时一致的姿态继续前行，成功实现攀爬台阶。

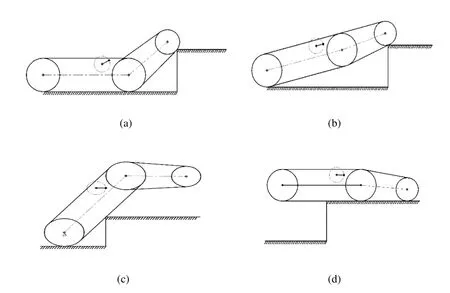
图4 机器人攀爬台阶过程

由上述越障过程可知，履带机器人质心的水平坐标与台阶外角线重合是机器人成功越障的临界条件[2]。图5为机器人越过台阶外角线时的临界状态图。此时摆臂处于水平状态，机器人的质心处于台阶外角线的垂线与机器人质心轨迹圆相切的切点。此种状态下，机器人的越障最为方便，因为其质心位置在摆臂姿态的影响下调整到最右侧，机器人只需要保持向前的驱动力，即可马上使车身完全脱离地面，实现越障。

图5 机器人攀爬台阶临界状态

根据机器人越障临界示意图以及临界条件，可以得到机器人的越障高度为：

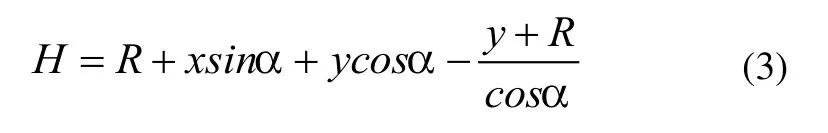
对于一定高度H的台阶，有一个对应的机器人仰角α；反之当机器人达到某个仰角α，有一个能攀越的最大高度H。当摆臂处于水平状态时，机器人仰角α与摆臂的摆角θ之间存在几何关系：α+θ=2π。

将机器人的参数代入式(1)和式(3)，可以得到台阶高度与机器人仰角的关系三维图。由图6可知，当α=48°时，Hmax=255.5mm。

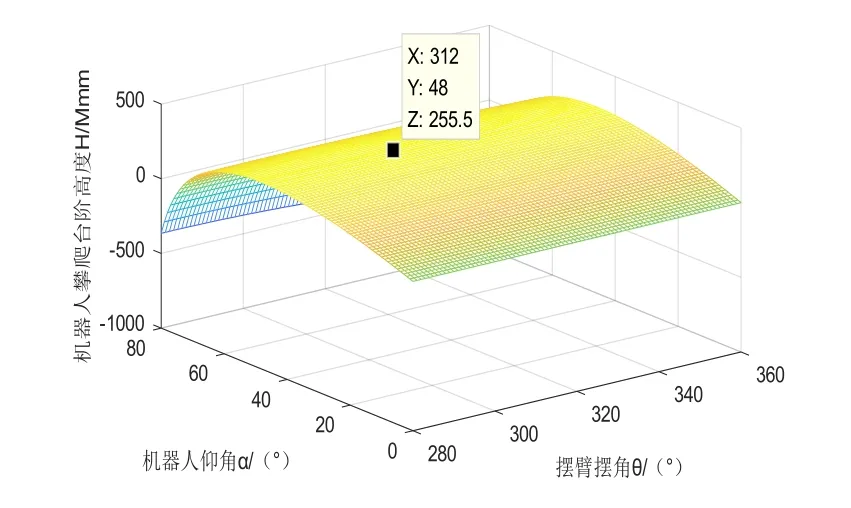
图6 可攀爬台阶高度与机器人仰角/摆臂摆角关系三维图

3.3 机器人跨越沟道

机器人跨越沟道的过程如图7所示。沟道的关键边界线为两侧边界线。从质心运动学的角度分析，当机器人的摆臂保持水平时，质心处于最靠前位置，此时跨越沟道最为有利。当质心运动到沟道的近侧边界线时，摆臂前端必须已经越过沟道的远侧边界线，保证机器人在下一时刻质心越过沟道近侧边界线时，有至少两个支点使得机器人不会因为重力而发生翻转。而且摆臂下侧履带需接地，尽可能保证质心靠后。设摆臂履带与中心线O2O3之间的夹角为β（本文校机中β=15°），此时须满足条件：D1= l3cosβ+ l0-x。当质心快通过沟道的远侧边界线时，机器人的主履带必须仍与沟道外部的地面保持接触，保证机器人在越过远侧沟道线之前，机器人不会发生翻转，而且摆臂此时必须保证水平，使质心尽可能靠前。此时须满足条件D2=x。综上，机器人能够跨越的沟道宽度D应该满足如下条件：D=min（D1， D2）。代入本文校机的结构参数。可以求得D1=528mm，D2=489mm。因此，机器人能够越过的沟道宽度最大值为D=min（D1，D2）=489mm。

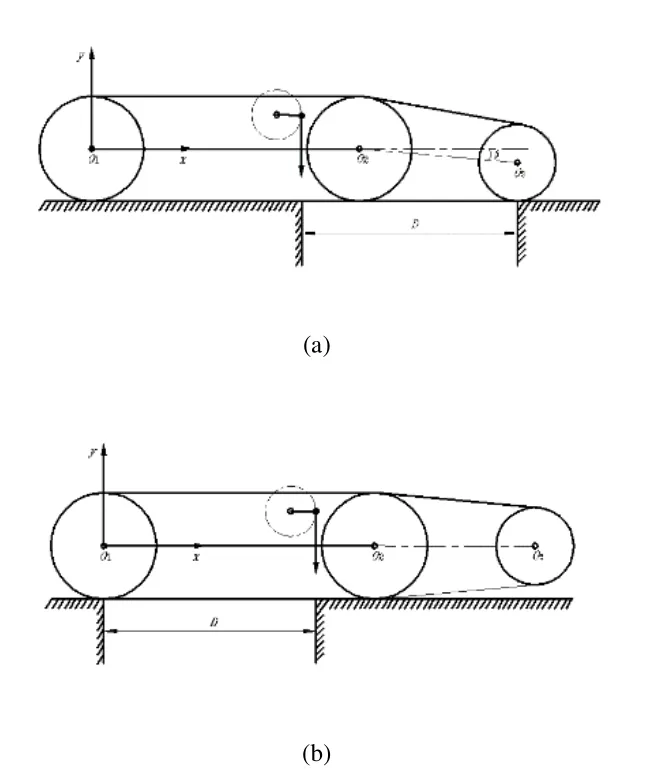
图7 机器人跨越沟道

3.4 机器人攀越台阶与沟道的组合地形

机器人在攀越台阶与沟道的组合地形过程如图8所示。图9为机器人越障成功的临界状态图。此时，机器人质心与台阶外角线的垂线相切，机器人后部履带处于与沟道近侧边界线脱离接触的临界状态。在下一时刻，机器人后轮会在前半部分重力的作用下脱离地面，机器人整体随之向下翻转至水平线，机器人后半部不发生卡阻现象。由图中几何关系，可以求出沟道近侧边界线与台阶外角线的水平距离L。

图8 机器人通过台阶与沟道组合地形过程

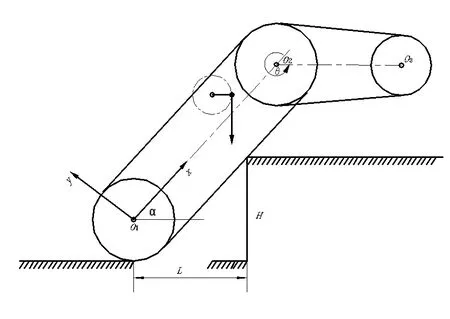
图9 机器人通过台阶与沟道组合地形临界状态图

将校机参数代入式(4)，机器人攀爬台阶高度、跨越沟道宽度与机器人仰角关系如图8所示。

由图可知，当机器人在越过最大的台阶高度255.5mm时，对应能跨越的沟道宽度为288mm。为了更直观的了解台阶与沟道组合地形下，攀爬的台阶高度与能同时跨越的沟道宽度之间的关系，联立式(3)与式(4)，作出台阶高度与沟道宽度的二维关系图，如图9所示。

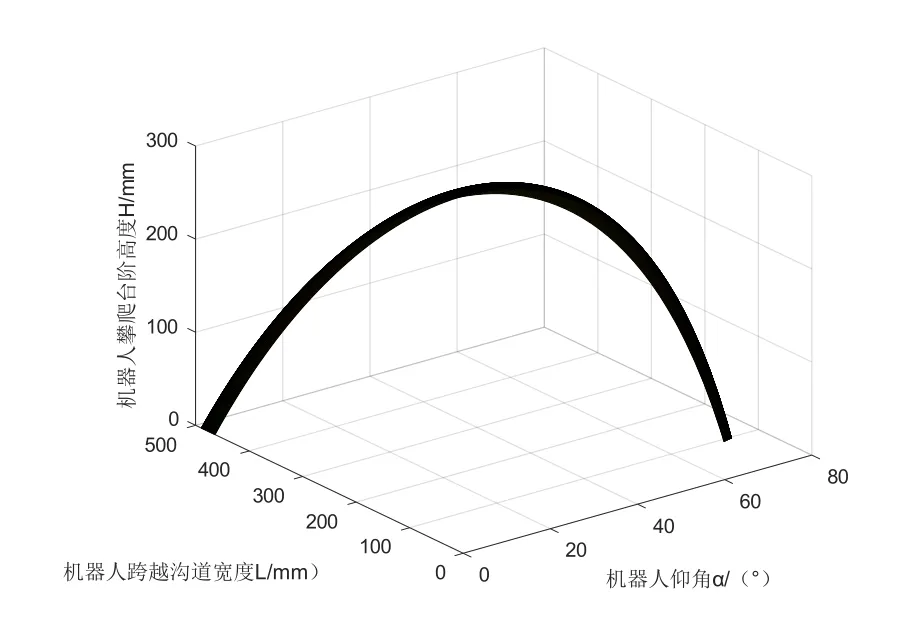
图10 台阶高度、沟道宽度与机器人仰角的关系三维图

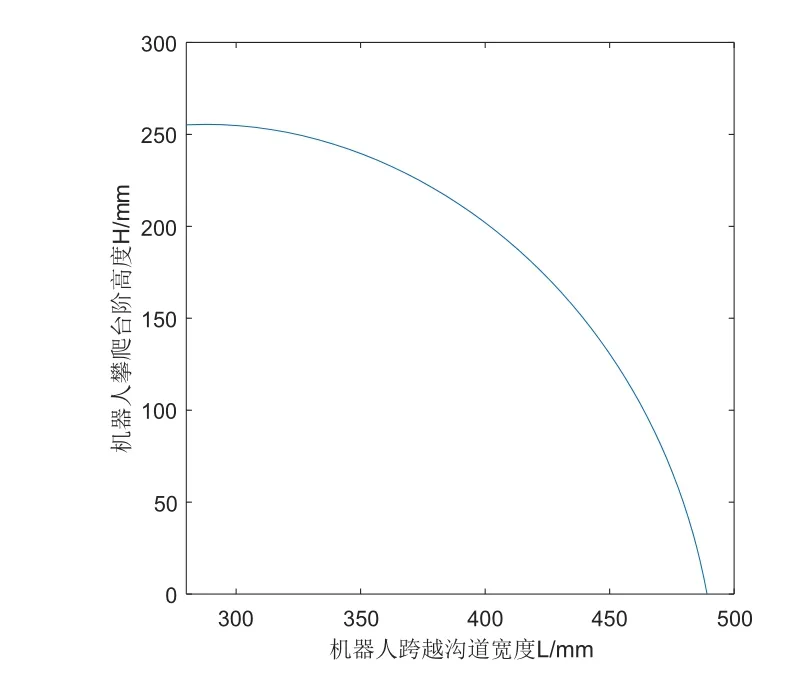
图11 台阶高度与沟道宽度关系二维图

4 结论

1）从运动学的角度，研究了机器人面对单一的台阶和沟道地形时的越障机理与越障能力。其越障的关键是机器人的质心能越过地形的边界线。

2）在1）的基础上，重点研究了机器人在面临台阶与沟道的组合地形时的越障机理：机器人质心越过台阶边界线之前，机器人后轮与水平面的切点必须保持在沟道的边界线外侧。

3）绘制了组合地形下，台阶高度、沟道宽度与机器人仰角的三维关系图，得出最大越障高度255mm下，沟道宽度不得大于288mm的结论。在此基础上绘制了台阶高度与沟道宽度的二维关系图。为机器人在通过台阶与沟道的组合地形时的通过性提供了理论依据。