让学习深度发生——《确定位置》教学实录与分析

张 缅

【教学内容】

苏教版四年级下册第八单元《确定位置》第一课时。

【教学过程】

片断一：情境导入，激活创造思维。

1.游戏引入，描述一维空间上任意点的位置。

师：（播放视频）在一片大森林里，可恶的光头强又开始乱砍滥伐了。同学们，怎么办？

生：报警。

画外音：（警察）各位居民请注意。有谁知道光头强的具体位置请立刻打电话给我。

根据语音提示在学历案上用你喜欢的方式画光头强的位置。

画外音：光头强跑到森林小道最右边啦！光头强跑到森林小道正中间啦！光头强跑到森林小道偏右的地方啦！

师：这次大家怎么找的地方不一样呢？

生：因为描述的不清楚。

师：那你能清楚地说出光头强的位置吗？你可以借助森林里的物体。

生：在第2 根电线杆旁。

师：有不同说法吗？

生：在第6 根电线杆旁。要明确方向。

师：给电线杆编号是个好办法。他俩说的都可以，在一条线上按习惯从左往右数。光头强现在的位置我们用6 来表示。（板书：6）

师：现在呢？（出示光头强移动到最左边）你也能用一个数表示吗？

生：0。

师：这是森林小道的起点，我们用0 表示。（课件显示并板书：0）

师：（出示光头强移动到4 和5 之间）现在他的位置呢？也用一个数表示。

生：4.5。（板书：4.5）

师：4.5 是什么数？小数也能表示位置。

师：（出示光头强移动到3 的位置）现在呢？（板书：3）

师：看来，光头强只要沿着森林小道跑，我们都能用一个数来表示他的位置。

【分析：游戏是学生喜欢的活动，创设游戏情境，其间不失挑战性元素，更能激发学生的参与欲。通过游戏回顾了一维空间中点的位置的描述方法。关注0 起点、数的顺序，明确直线上任意一点都有唯一的一个数与它对应。为描述二维空间中点的位置打下基础。】

2.情境激疑，创设平面中任意点造成描述障碍。

师：狡猾的光头强可没有那么容易让你们抓到。接下来他跑到了密林深处。看，光头强出现了。这个圆点就代表他。他现在的位置谁能说说？

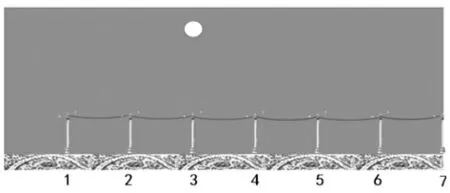
生：3 的前面。

生：3 的正前方。

师：看来，大家都认为光头强的位置在“3 的正前方”。（板书）

师：你觉得警察凭这样的线索能准确地找到光头强吗？

生：不行。3 的正前方有一条线。

师：上来指指你说的一条线。

师：这条线上无数个点都在3 的正前方是吧？说明信息不够全面，有点模糊。（教师在“3 的正前方”下面板书“模糊”两字）

【分析：密林深处的这个点位置如何确定？从确定直线上点的位置到确定平面上点的位置，学生发现用原有方法描述的信息是模糊的，于是形成了认知冲突，促使他们去寻求新的方法。学生的思维水平参差不齐，有的停留在一维水平，有的已经在二维空间考虑这个问题。但课中，不管哪个层次的学生，都围绕着核心问题努力地思考并寻求问题解决的策略和方法，都不同程度地提高了自己原先对位置表示的理解，优化自身的知识结构。】

片断二：任务驱动，尝试自主建构数学知识。

1.实践操作，自主建构直角坐标系（雏形）。

师：那么，光头强准确位置的信息该是怎样的呢？请同学们小组合作研究一下。

合作要求：

（1）独立思考：想办法帮警察找到光头强准确的位置。（可以量一量、画一画、标一标）

（2）合作交流：把你的办法在小组里交流。

生：我量了圆点到森林小道的距离是2 厘米。

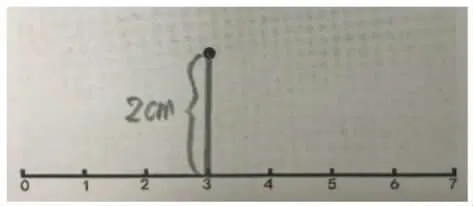
师：光头强准确的位置在哪？

生：在3 的正前方2 厘米处。（板书：3 的正前方2 厘米处）

生：要是能在图上竖着放一把尺就好了。

生：我在森林的左边标上了数字。从光头强现在的位置对着横轴和竖轴上相应的数字画横线和竖线，这样看得更清楚。

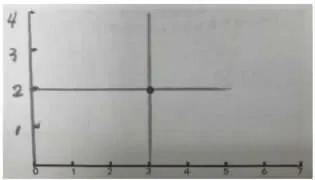
师：要是在6 的上方3 格呢？用你的方法找一找。

生：要是光头强跑到很多地方，用这样的方法都能很快找到，在图上会形成格子。

生：我不仅画了竖的线，还画了横的线，标上刻度。这样看起来就更方便了。

师：你为什么要这样画？

生：竖线为了方便看出光头强在小路几的上面，横线表示离底边的距离。

师：大家的方法各不相同，但都找到了光头强的准确位置（在3 的正前方2 格处）。这样的信息告诉警察你认为怎样？因为它很——准确（板书“准确”）。

……

【分析：创设了一个开放性的大问题，让学生自主探索，想办法确定二维空间里点的位置。由于学生认知起点、思维水平有差异，他们会形成不同层次的思考过程。教师有序地组织学生阐述自己的想法，反思自己的方案，其他学生反驳、争辩并优化方案。在思维的碰撞中通过集体智慧的共同努力，完成确定位置从一维到二维的突破，逐步创造出平面直角坐标系（第一象限雏形）。这正是本堂课最大的创新点，生动紧凑的互动过程中，有质疑、有补充、有尊重、有完善，成功地实现了“再创造”。】

2.规范约定，用数对表示平面上点的位置。

师：老师也学你们用电脑画画看。（1）横竖画线标刻度；（2）竖线表示列，从左往右分别叫第一列、第二列……以此类推；（3）横线表示行，从下往上分别叫第一行、第二行……以此类推。光头强的位置是——

生：第三列第二行。

师：在数学上我们可以用数对表示第三列第二行。［板书：数对。出示（3，2），读作：数对三二。］数对规定先列后行，它更加简洁。

师：熊大也来到森林。谁能说说它的位置呢？用数对表示呢？它表示什么？

生：数对（2，3），表示第二列第三行。

师：观察数对（3，2）和数对（2，3），你有什么想说的？

生：数相同，意义不同；行数和列数相反。

师：你觉得数学家规定数对先列后行有道理吗？

师：熊二也要来抓光头强。它的位置在（5，4）。谁能点出它的位置？表示什么？

【分析：在学生理解了数对（3，2）后，巧妙呈现数对（2，3），学生在观察、对比、说理过程中体会到规定数对有序性的必要以及数对中两个数各自的含义，更深刻地认识了用有序数对来确定位置的本质。】

片断三：对比反思，明晰二维描述的核心要素，建立有序数对与平面上任意点的对应关系。

师：回顾刚才的研究过程，你认为确定光头强在密林深处中的位置和森林小道上的位置有什么不同？

生：森林小道在一条线上，用一个数就可以确定位置；密林深处是一个面，要用两个数才能确定位置。

师：两个数能确定平面上所有点的位置吗？那要是他跑到（8，3）呢？还能找到位置吗？

生：可以把射线延长。

师：（10，8）呢？（20，30）呢？屏幕外有没有这样的位置呢？

师：要是在这个位置呢？

生：把格子画得再密一点。

生：用两个小数能表示。

师：在这张坐标图里可以画无数条横线和竖线，看来这样的方法能快速精确地确定这个平面任何一个点的位置。

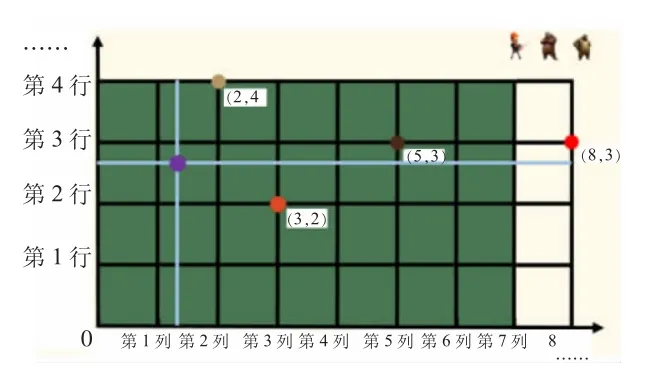
【分析：对比确定森林小道和密林深处中点的位置不同之处，其实就是厘清在一维空间与二维空间里确定点的位置的本质。通过这个活动学生进一步明确确定二维空间中点的位置的核心要素是“列”和“行”这两个信息的有序组合，提升了他们的思维能力和空间想象力。教师创造性地设计了确定网格外部以及单位小格内部点的位置的环节，打开了学生想象的空间，感悟横轴、纵轴可以无限延长，网线可以无限增加，平面内任意一点都能用有序数对来确定位置。这样的探究活动，学生不仅学会了用数对确定位置的方法，而且创造性思维、实践能力也得到发展。】

片断四：课堂延伸。

师：光头强见居民们用数对很快就能找准他，于是借助直升机逃跑了，居民们用这样的数对真的再也找不到他了。聪明的同学们，你知道光头强逃到哪里了吗？大家课后可以继续思考或查阅资料。

【分析：最后创设了一个悬念帮助学生将视野从平面的点拓展到空间中的点，也就是从二维向三维发展。相信有了一维向二维发展时的探究经历及思维方式作为基础，他们一定能顺利地拓展到三维空间。】