考虑成层地基的黏弹性人工边界模型

尹 刚, 赵兰浩, 李同春

(1.河海大学水利水电学院,江苏 南京 210098; 2.河海大学农业工程学院,江苏 南京 210098)

天然地基为一半无限域,采用有限元等数值模拟方法进行动力计算时,需从半无限域的地基中截取有限的区域进行计算,并在截取区域的边界上施加一定的人工边界条件,使得地震波传递到边界时不再发生反射,以模拟无限地基对于地震波的辐射阻尼效应[1-2]。在众多种类的人工边界条件中, Andrew[3]提出的黏弹性人工边界条件能同时模拟散射波的吸收和半无限地基的弹性恢复能力,且易于编程、稳定性好,得到了广泛的应用。

地震动输入方法一直是研究土-结构相互作用的关键问题之一[4-6]。黏弹性人工边界采用波场分离的技术,将波动问题转化为人工边界处等效荷载的计算问题[7]。等效荷载的计算需要求解人工边界上的自由场,传统的求解方法为延迟法,认为人工边界点的自由场与入射波场存在行波效应,相位差可由人工边界点到入射边界的距离和波速求出[8]。而这种行波效应的存在,也对结构动力响应产生了一定的影响。吴健等[9]分析了拱坝的随机地震行波效应,李悦良[10]研究了行波效应对地震反应谱的影响,赵博等[11]分析了行波效应对多跨大跨结构的随机振动响应的影响,范重等[12]分析了超长结构地震行波效应的影响因素。

当地震波穿过不同的介质时,会发生反射与透射,当两层介质的波阻抗不同时,反射波与透射波的振幅与原入射波一般是不相等的,且会存在波型转换等问题[13]。传统的延迟法只能考虑波速的影响,不能考虑振幅的改变和多次反射波及透射波的叠加,因此对于成层地基条件,需要进一步推导适用于成层地基的地震波输入模式。为此,本文推导了适用于成层地基的考虑波一次反射透射的等效荷载计算公式,以解决水平成层地基的波动输入问题。

1 地震波入射时的反射和透射系数

地震波穿过两个波阻抗不同的土层时,会在两种介质的分界面上发生反射与透射,透射波会在继续向上传播,而反射波则会反射至下部土层往下传播。不同类型的波产生的反射波和折射波的类型也不同,P波、SV波和SH波入射时可能发生的反射折射情况[14]见图1(图中下标1、2分别表示第一层和第二层;下标i、r、t分别代表入射波、反射波和透射波;下标P代表P波,SV代表SV波,SH代表SH波;A为振幅;θ为波传播方向与介质分界面法向的夹角;cP和cS分别为纵波波速和横波波速)。

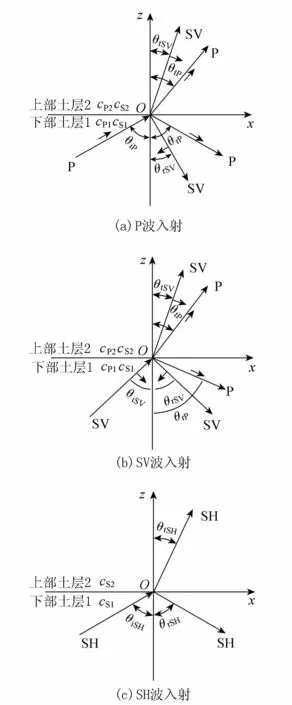
图1 3种波入射时波型转换情况

设上下两层介质纵波和横波波阻抗之比分别为

(1)

式中:αP和αS分别为纵波和横波的波阻抗之比;ρ1和ρ2分别为下部土层和上部土层的密度。

以P波为例,由分界面处的位移应力协调条件,可得波幅比的方程组为

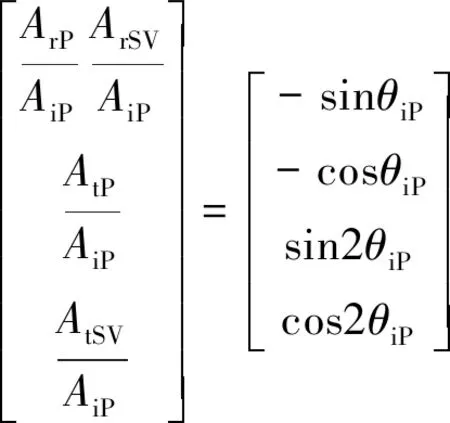
(2)

由于工程中一般都假定地震波是垂直入射于地基底部的,故主要讨论地震波垂直入射的情况,即θiSV=θrSV=θtSV=θrP=θtP=0,代入式(2)可得:

(3)

式(3)的结果表明,当P波垂直入射时,反射SV波和透射SV波的振幅为0,即没有发生波型转换,反射波和透射波依然为P波。同时,当界面为自由表面时,令ρ2=0,可得:

(4)

即P波垂直入射至自由表面时,透射波为零,即不存在透射波;反射波波幅大小与入射波相等,方向与图中规定的正方向相反即与传播方向相反,最终在顶面入射波和反射波的振动方向相同,即自由表面的位移放大2倍。

同样地,采用上面相同的方法可以得到SV波入射时的波幅比方程组,当SV波垂直入射时,可求得波幅比为

(5)

对比式(5)和式(3)可以看出,当波垂直入射时,P波和SV波的反射透射规律相似,不发生波型转换,波幅比的大小与波阻抗相关。当界面为自由表面时,令ρ2=0带入上式可得出与P波相同的结论,即自由表面的位移呈放大2倍的规律。

SH波的反射透射较为简单,因为SH波仅有垂直于入射面的位移分量,即不会发生波型转换;当SH波垂直入射时,波幅比计算公式与SV波相同(式(5));与P波和SV波不同的是,当界面为自由表面时,无论SH波以何种角度入射,自由表面位移均为放大2倍。

2 考虑波一次反射和透射的等效荷载计算

对于层状地基模型,当地震波从底部入射后,传播到分界面处会发生反射和透射,反射波会向下传播在人工边界处被吸收。向上传播的透射波在到达下一层的分界面后会再度产生向下传播的反射波,当新的反射波到达分界面时会再度发生反射和透射,透射波向下传播至人工边界被吸收,反射波重新向上传播至自由面。因此,地基中将不断发生反射和透射的过程。实际情况中,一般地震动的持续时间较短,且需要考虑地基的阻尼,故主要考虑地震波在每一层的一次反射透射的过程[15]。

黏弹性人工边界节点Q处在t时刻的等效荷载为

KQωQ(xQ,yQ,t)

(6)

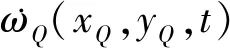
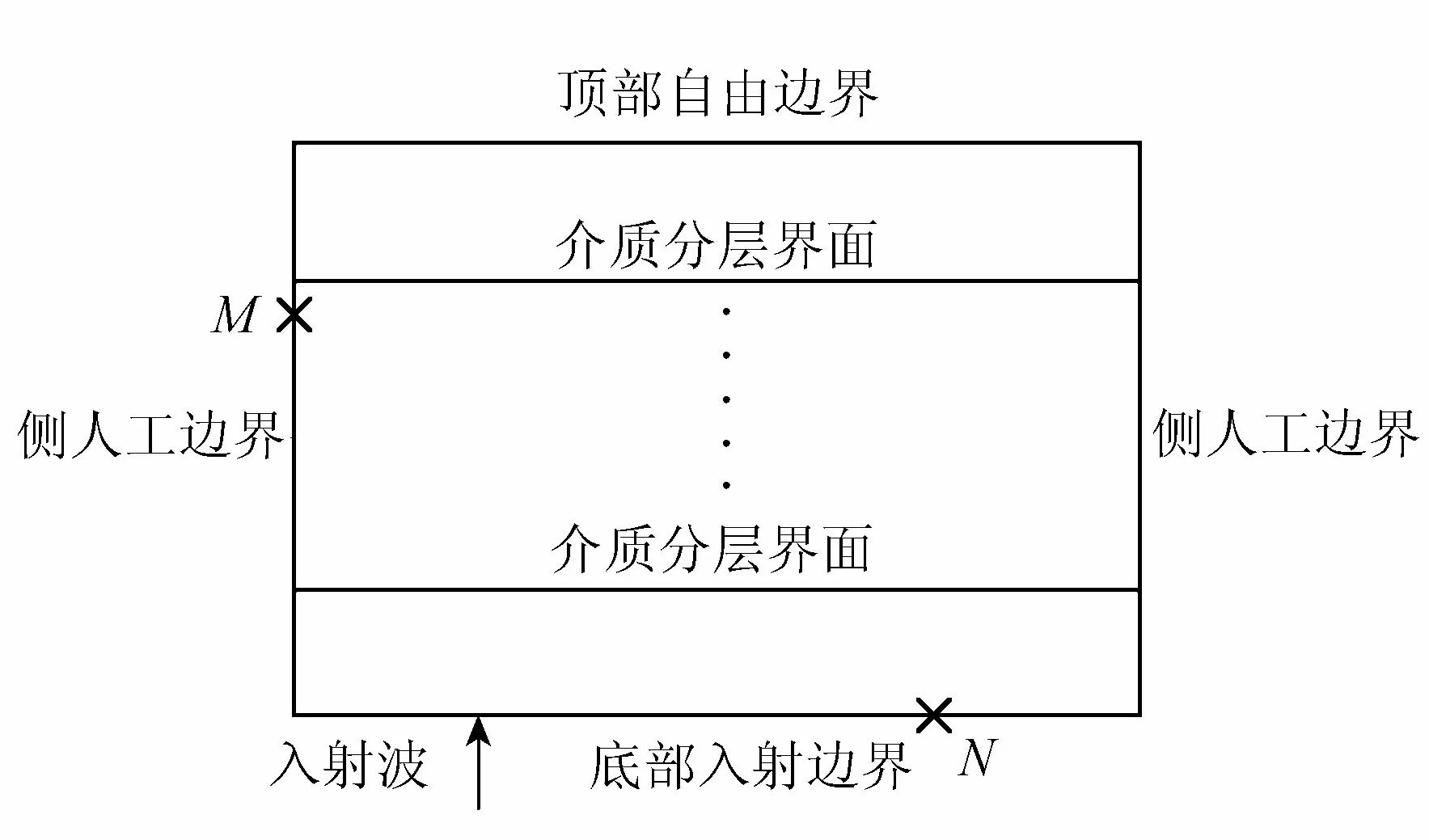
图2 层状地基模型

对于侧边界,可以通过反射和透射系数,根据延迟法求得相应的自由波场,进而求得相应的等效荷载。对于侧边界的M点而言,可以将波的入射过程分为以下3部分:

a. 入射波还未到达M点。此时M点的自由波场位移为零。

b. 入射波到达M点,这一层顶部的反射波还未到达M点。这个阶段M点的位移由入射波场经过多层透射后产生,要考虑每一层的透射作用对幅值的影响。

c. 入射波到达M点,这一层顶部的反射波也到达M点。这个阶段M点的位移由入射波和反射波两部分叠加而成,入射波需考虑多层透射的影响,反射波由入射波在顶部反射而来,需要考虑反射作用对幅值的影响。

上述3部分可以总结为以下计算公式,为方便表述,令反射系数为β=Ar/Ai,透射系数为γ=At/Ai,则侧边界上一点M的自由波场位移计算公式为

(7)

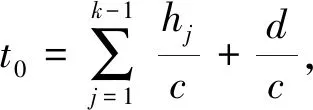
对于底边界,自由波场即为入射波场,即

ωN(xN,yN,t)=ω0(t)

(8)

由式(7)和式(8)即可确定人工边界的自由波场,代入式(6)中即可求出人工边界上的等效荷载大小,完成地震波的输入。

3 算例分析

3.1 考虑成层地基的波动输入方法验证

对成层地基的波动输入方法编制了相应的计算程序,通过两个算例进行验证。选取如图3所示的两层地基模型,坐标原点设为B2点,截取有限的部分进行计算,下层地基编号为①,上层地基编号为②。考虑3个计算方案：方案1为成层地基模型,考虑地震波在分界面处的反射透射过程;方案2为成层地基模型,不考虑地震波在分界面处的反射透射,只考虑不同层地基的波速影响;方案3为均质地基模型,上下两层的波阻抗相同,不存在反射透射过程。3个计算方案中,两层地基密度均为2 000 kg/m3,泊松比为0.25,弹模的取值考虑不同的计算方案,前2种方案上层地基弹模为2 GPa,下层地基为10 GPa,第3种方案上下层地基皆为2 GPa。

图3 两层地基计算模型(单位：m)

第一个算例假定从地基底部垂直入射一单周期SV波,位移时程如式(9)所示,位移最大值为1.3 m,周期为0.5 s,时间步长设为0.000 1 s,总计算持时为5个周期即2.5 s。坐标原点设为顶部中心点,图3中4个特征点B1(-200,0)、B2(0,0)、B3(-200,-200)和B4(0,-200)为观测点,计算得到方案1中各点的位移时程曲线如图4所示,各计算方案下B1点和B3点的位移时程曲线如图5所示。

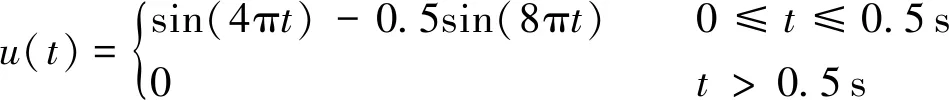
(9)

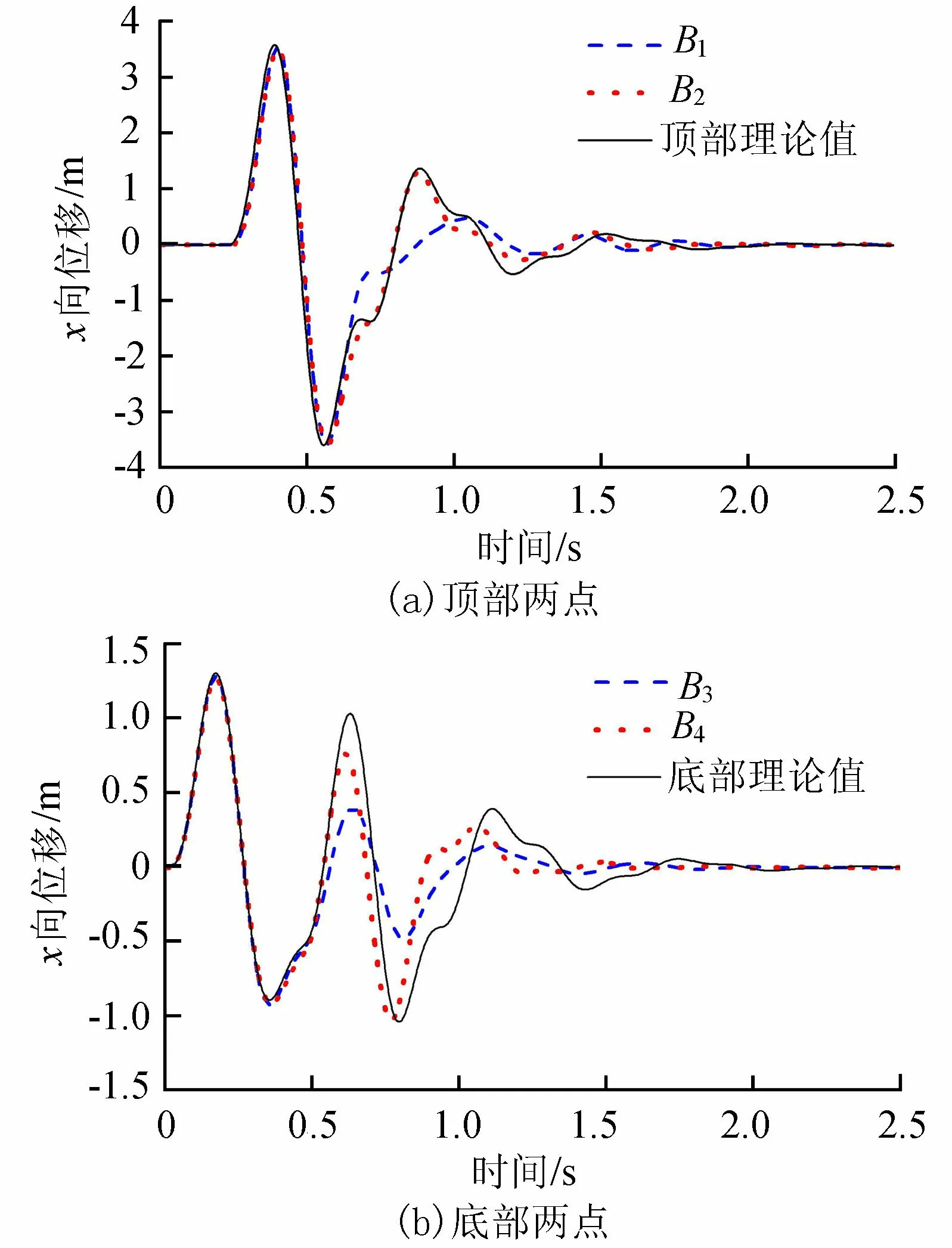
图4 方案1各观测点的x向计算位移与理论值的对比

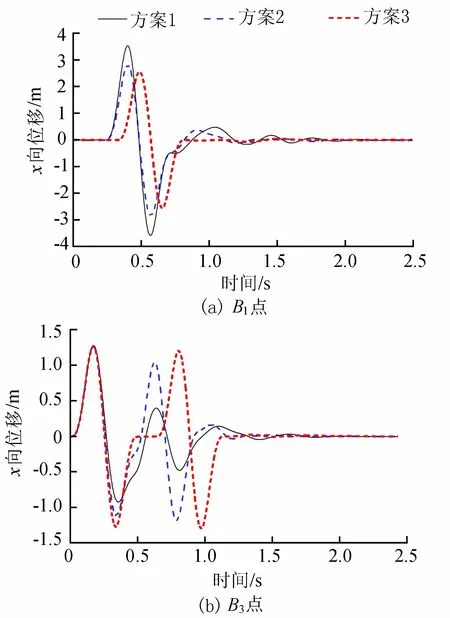
图5 各方案B1点和B3点的x向计算位移时程曲线

分析图4,由透射系数公式可知上层地基的透射系数为1.38,地震波经过透射到达顶部放大两倍后最大位移的理论值为3.58 m,顶部B1、B2两点第一个周期内的x向位移最大值为3.51 m,与理论值接近;底部B3、B4两点的最大值为1.283 m,与输入波接近,满足精度要求。传播规律上,在第1个周期内,同一高程上的B1、B2两点和B3、B4两点位移响应几乎重合,顶部B1、B2两点的位移响应具有延迟效应,第1个周期内最大值达到的时刻为0.396 s,底部B3、B4两点的最大值达到的时刻为0.168 6 s,两者时间差为SV波传播的时间,符合波的传播规律。

对于上层地基,透射波在顶部反射到达分界面后再次发生反射与透射过程,反射波向上传播,透射波向下传播至下层地基,由于侧边界的波动输入仅考虑了一次反射透射过程,分界面处产生的二次反射波在侧边界逐渐被吸收,位于侧边界的B1点的位移响应出现了小于B2点的情况。对于下层地基,在第1个周期的后半期,随着分界面处反射波向下传播,B3、B4两点的位移由入射波和反射波叠加而成,此时入射波产生的位移与反射波方向相反,因此B3、B4两点的负向位移大小减小;0.457 s后,分界面处发生二次反射透射的透射波传播至底边界,此时入射波、第1次的反射波和第2次的透射波产生叠加效应,出现了第2个波峰。同样地,由于侧边界的波动输入仅考虑了一次反射透射的过程,多次反射透射产生的散射波在侧边界被吸收,因此B3点的位移响应要小于B4点。对于整个系统而言,由于人工边界单元的存在,多次透射与反射产生的散射波最终被边界单元所吸收,体现了无限地基的辐射阻尼效应。

比较各点计算时程曲线与理论值,对于顶部各点而言,时程曲线规律与理论值基本吻合,满足工程中抗震分析的要求。其中,B2点相对于B1点而言误差更小,这是因为B1点位于侧边界,人工边界上的位移与地震动输入方法直接相关,只考虑一次反射透射过程产生的误差在人工边界上产生的影响要大于远离人工边界的地方。对于底部各点而言,在单周期内,数值计算的结果与理论解基本吻合。时程曲线产生较大误差的地方为顶部的反射波穿过分界面发生再次透射时。综合考虑顶部和底部位移响应,本文主要考虑波一次反射透射产生的误差都没有发生在最大响应时刻,且时程曲线的发展规律与理论值基本一致。由于工程中主要关心上部结构的最大地震动响应和动响应的时程规律,顶部响应的精度满足工程设计的要求。

分析图5,各计算方案下B1、B3两点的位移时程曲线差异均较大。方案1与方案2由于都考虑了波速的影响,因此两者得到的时程曲线频率和相位相同,但振幅不同。对于B1点,方案1的最大位移响应要大于方案2;对于B3点,由于方案1考虑了波在分界面处的反射,因此方案1中到达底部的反射波为分界面处的反射波,方案2中为顶部的反射波,两个方案得到的响应在方案1中的反射波到底部后出现了较大的差异。方案3的传播规律与均质地基的传播规律相同,也侧面验证了黏弹性人工边界单元的适用性,但地震波到达顶部的时间比方案1和方案2都偏迟,无法真实地模拟地震波的传播过程。振幅方面,对于顶部而言,方案1考虑了波的反射与透射,地震波向上传播到达顶部时经历了分界面和顶部自由面两次放大过程,而方案2和方案3都只考虑了顶部自由面的放大过程,最大位移响应都偏小。

综上,相比于方案1,方案2虽考虑了波速的影响即相位的影响,但振幅与理论解相差较大,不能真实地反映地震波的放大效应;方案3则表明成层地基若按均质地基处理,不仅振幅与理论解相差较大,地震波的延迟效应也不能更全面地得到考虑。因此,方案1能比方案2和方案3更好地用于成层地基的波动问题分析,满足工程抗震分析的精度需求。

第2个算例同样基于图3的计算模型,考虑从底部输入EL波N-S向时程,输入的位移时程曲线和速度时程曲线如图6所示,计算总时长为53.72 s,时间步长为0.04 s。参考第1个算例的结果,第2个算例只采用第1个方案进行计算,得到B2点的位移时程曲线如图7所示。

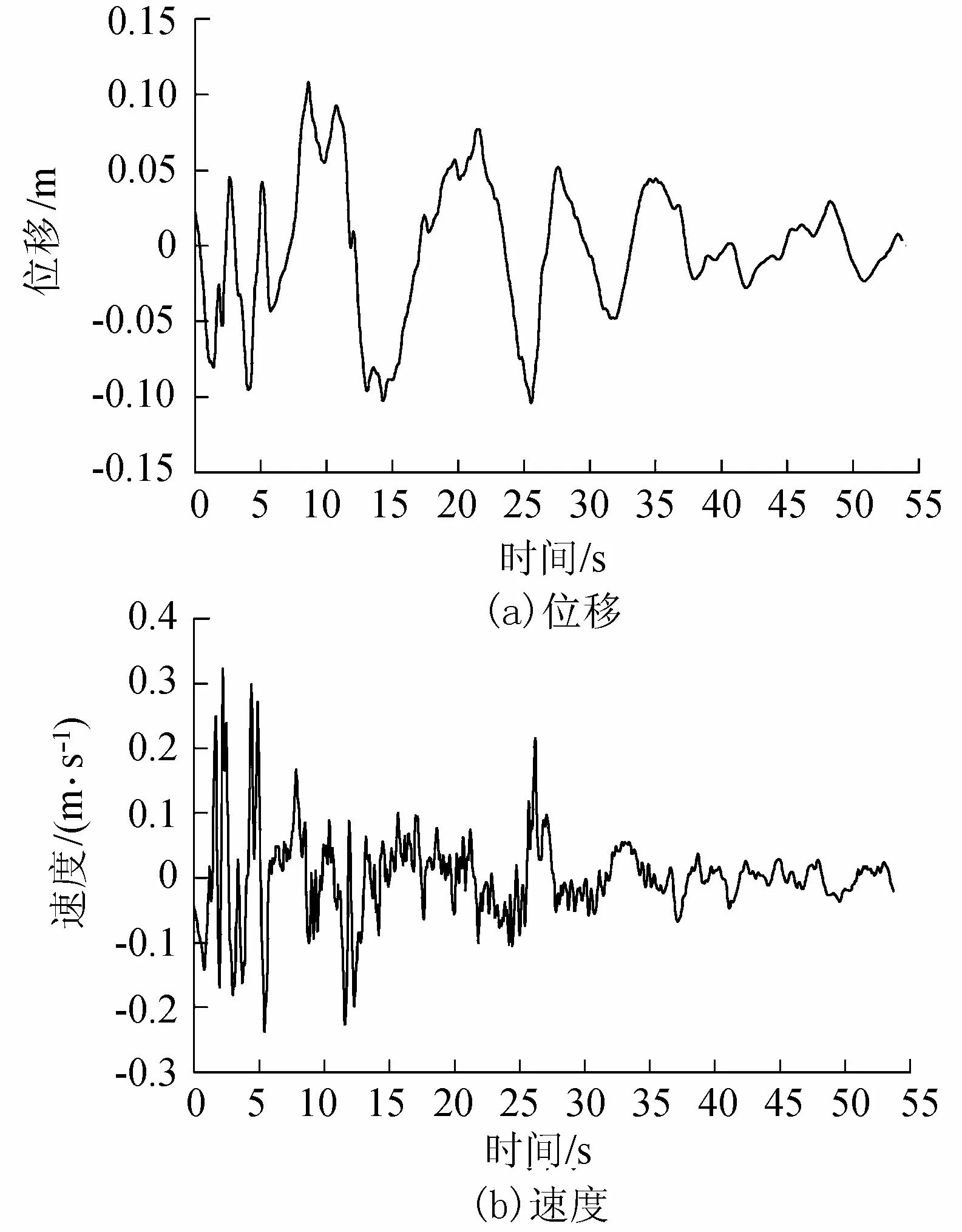
图6 输入的EL波位移与速度时程曲线

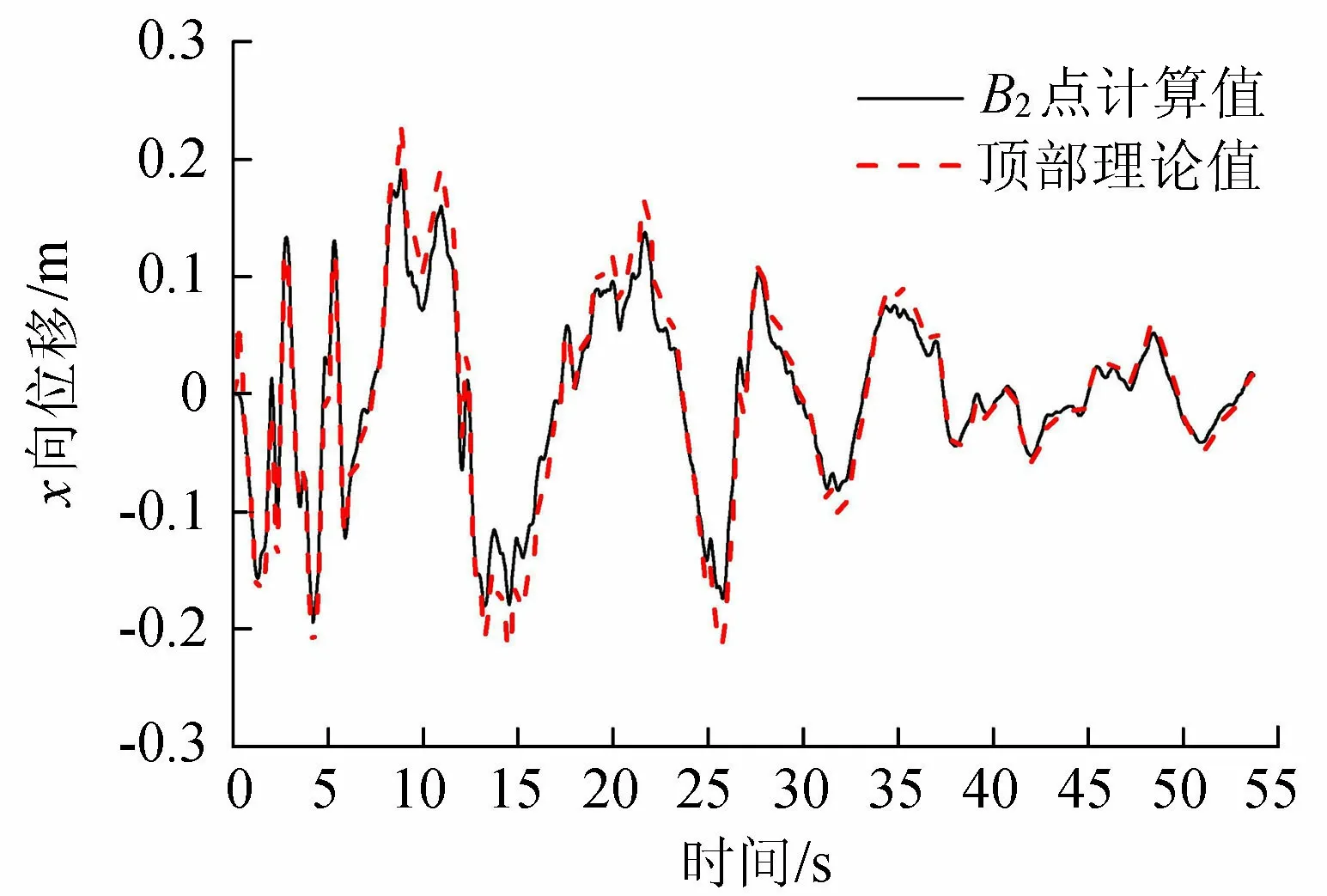
图7 顶部观测点的x向位移计算与理论值时程曲线

分析图7,顶部的x向位移响应与理论值变化规律相同,波峰波谷出现的时刻基本一致。位移幅值上,B2点位移的正向最大值为0.221 m,对应的理论正向最大值为0.223 m,误差在1%以内;负向最大值为-0.216 m,理论值为-0.215 m,误差在1%以内。综合算例1和算例2,本文提出的考虑一次反射透射的成层地基波动输入方法满足工程设计的需要。

3.2 成层地基重力坝的地震动响应分析

某重力坝坝高100 m,坝顶宽度15 m,坝底宽度70 m,下游坝坡坡度1∶0.7。地基范围沿上下游方向各取3倍的坝高,深度方向考虑3层地基的影响,每层地基各为100 m，即总深度为3倍的坝高,坐标原点设在坝底中点,选取坝顶中点D1(-22.75,100)、坝踵D2(-35,0)和坝趾D3(35,0)三点为观测点,模型如图8所示。假定从底部垂直输入SV波,输入的人工波依据规范给出的设计反应谱合成,设计地震动峰值加速度为0.1g,地震动持时为15 s,时间步长取为0.01 s,人工波时程曲线如图9所示。

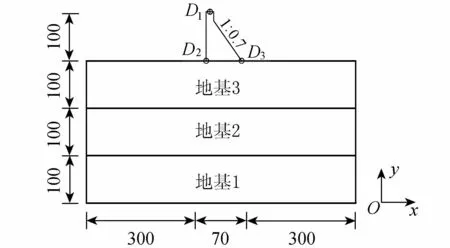
图8 重力坝计算模型(单位：m)

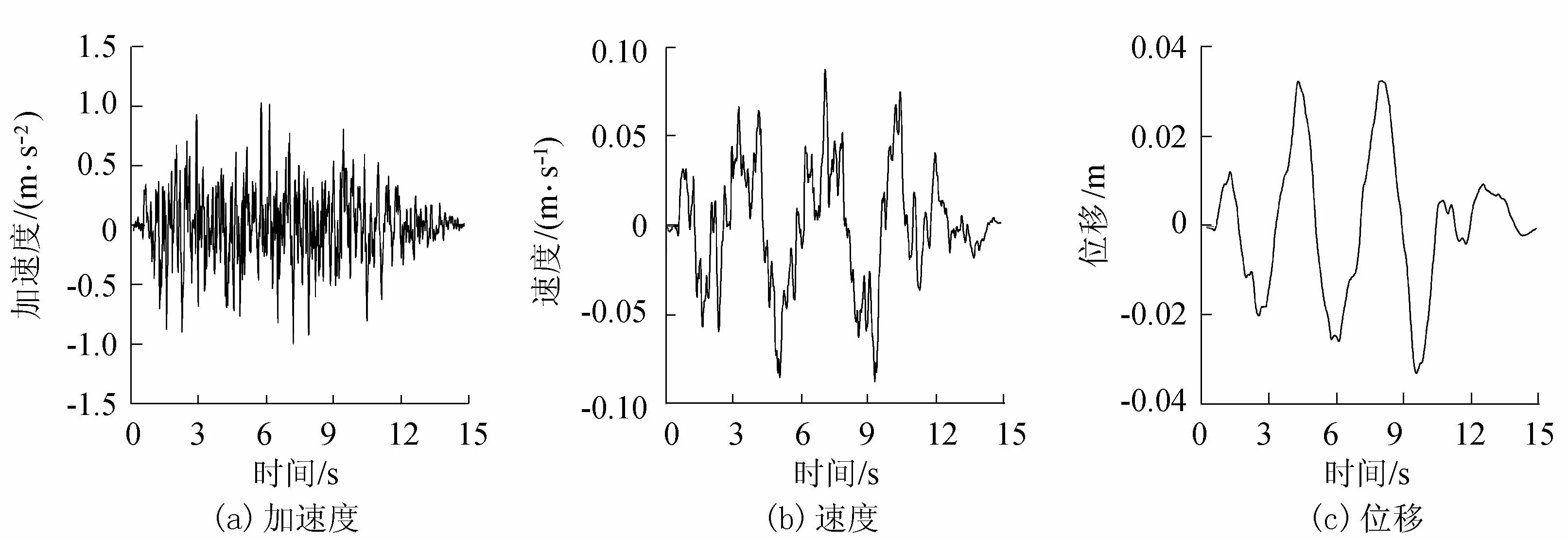
图9 输入的地震波加速度、速度、位移时程

图10 各计算方案D1点x向加速度时程曲线

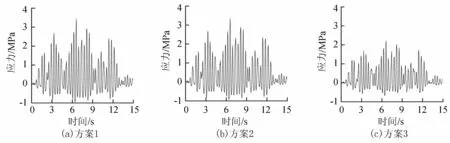
图11 各计算方案D2点第1主应力时程曲线

坝体混凝土动弹模为30 GPa,密度为2 400 kg/m3,泊松比为0.167;地基从下往上编号,3层地基的密度皆为2 700 kg/m3,泊松比皆为0.25,地基弹模从下层至上层依次为40 GPa、30 GPa和20 GPa。计算考虑3种地基模型(分别对应3个方案),第1种考虑地基为3层成层场地模型,波动输入考虑地震波的反射与折射,每层地基的材料参数按实际情况取值;第2种为成层场地模型,不考虑地震波在分界面处的反射与折射,只考虑波速的影响;第3种按传统的情况来处理,将地基简化为均质模型,材料参数统一取为与最上层相同,地基弹模为20 GPa。计算得到各种计算方案下D1点的加速度时程曲线、D2点的第1主应力时程曲线和D3点的第3主应力时程曲线如图10～12所示。

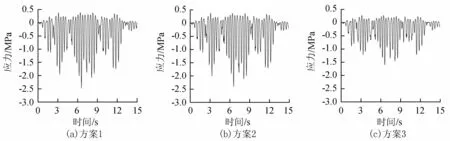
图12 各计算方案D3点第3主应力时程曲线

由图10～12可知,不同计算方案下坝体结构的动力响应有一定的差异。最大加速度和最大主应力都出现在方案1中,方案1得到的时程曲线振动范围比方案2和方案3都要大,这是因为方案1考虑了地震波在不同介质分界面处的反射与透射,输入的地震波振幅在传播过程中被放大,因此结构的响应也较大,这与前一节的算例结果相吻合。整体而言,考虑了成层地基模型的方案1和方案2得到的响应比较接近,且都大于按均质地基考虑的方案3,但方案2的结果在峰值响应上仍比方案1小3%左右,考虑到结构的复杂性和工程的重要性,对于高坝的抗震设计仍应采用方案1比较合理。在相位差方面,由于地基的波速较大,各方案得到的时程曲线相位差并不明显。

对比3种计算方案可知,按成层地基模型来进行动力分析,能更好地反映结构的地震动放大效应。而实际中,地基的分布情况更为复杂,地震波在各层之间的反射透射次数也更多,经过多次放大后,结构的动力响应也更为复杂,同时每个计算方案中,最大主应力都出现在坝踵处,所以对于重力坝而言,坝踵处的应力情况应在抗震设计中应着重关注。

4 结 论

a. 针对成层地基模型,以地震波垂直入射为例,基于波动理论推导了考虑地震波一次反射透射的等效荷载计算公式,建立的考虑成层地基的黏弹性人工边界模型,经以两层地基的SV波垂直入射算例验证,本文的波动输入方法合理可行。

b. 将考虑成层地基的黏弹性人工边界模型应用到重力坝的动力计算中,计算结果表明,均质地基模型的处理方法低估了成层地基的地震动放大效应,无法得到结构的真实地震动响应。在层状地基各层的材料参数相差较大时,应采用更为精确的成层地基模型考虑土-结构的相互作用,更有利于水工建筑物的抗震设计。