基于数学模型构建与应用基础上的数学核心素养的培养

☉江苏省海门中学 陆 娟

数学教育因为教育信息化的迅速发展而逐渐形成了运用数学知识解决实际问题的这一趋势.利用数学知识建立数学模型并解决实际问题是培养学生数学核心素养能力的重要手段，也是化抽象为具体的有效措施.数学建模其实就是运用数学思维对各个事物之间的关系和规律进行观察、分析以及用数学语言来表达与呈现.本文结合具体的数学案例谈谈几种常见数学模型的建构与应用.

一、三角函数模型

常见的三角函数模型：（1）正弦型函数模型y=Asin（ωx+φ）+b（A＞0，ω＞0）；（2）余弦型函数模型y=Acos（ωx+φ）+b（A＞0，ω＞0）；（3）正切型函数模型y=Atan（ωx+φ）+b（A＞0，ω＞0）.

例1已知函数（x∈R）.

（2）求f（x）的最小正周期及单调递增区间.

探析：这是三角函数中关于“数”的一道练习，建构已经学过的正弦型、余弦型、正切型函数模型可以对此类题目中的定义域、值域、最小正周期等问题进行求解.

解析：（1）则

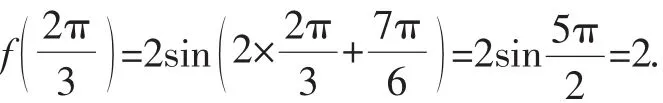
（2）因为ω=2，因此（fx）的最小周期.由2kπ-

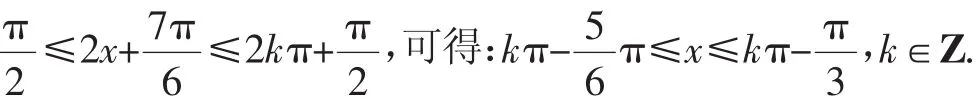
故f（x）的单调递增区间为

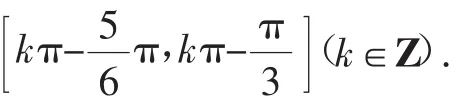
二、立体几何模型

教师在教学中应善于引导学生从现实生活中抽象出几何模型并强调数学建模的学习价值与意义，使学生能够在运用数学建模方法来探索与解决实际问题的过程中积累更多的经验，并在提升学生数学学习的积极性的同时令学生的数学建模能力也得到发展.

例2如图1所示，某工厂需要建一个仓库，要求仓库上部的形状为正四棱锥P-A1B1C1D1，下部的形状为正四棱柱ABCDA1B1C1D1，并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.

（1）若AB=6m，PO1=2m，则该仓库的容积是多少？

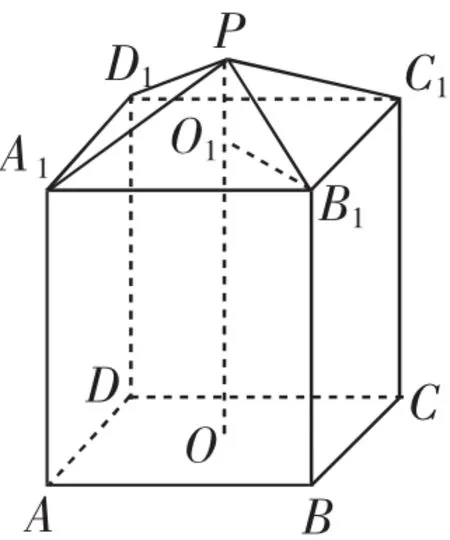
图1

（2）若正四棱锥的侧棱长是6m，则当PO1为多少时，仓库的容积最大？

模型建构探析：从问题2出发并以PO1为自变量建立体积的函数关系式.该仓库涉及的两种几何体的底是相同的，都为正方形，联想到正四棱锥的高与底面边长，用PO1=h来分别表示正方形边长及柱体的高H=4h，两者的底面积都是x2=2（36-h2），结合柱体、锥体的体积公式得，联想到利用导数来对其最值进行研究.当有最大值.

解析：（1）由PO1=2，知OO1=4PO1=8.

因为A1B1=AB=6，因此正四棱锥P-A1B1C1D1的体积

正四棱柱ABCD-A1B1C1D1的体积V柱=AB2×OO1=62×8=288（m3）.

所以仓库的容积V=V锥+V柱=24+288=312（m3）.

（2）设A1B1=am，PO1=hm，则0＜h＜6，|OO1|=4h.连接O1B1.

因为在Rt△PO1B1中

因此可得a2=2（36-h2）.则仓库容积V=V锥+V柱=a2·4h+

利用导数或不等式放缩即可求得其最值，当PO1=时，仓库的容积最大.

素养教学评析：从图1中很快就可以观察出仓库的容积即为正四棱锥与正四棱柱容积之和，学生由此也可以较为容易地构建出数学模型并令本题得以解决.

三、向量模型

建立向量模型并借助于空间向量的运算能够很好地解决涉及空间角度的很多问题.

例3如图2所示，在四棱锥P-ABCD中，底面ABCD是正方形，平面PAD⊥平面ABCD，点M在棱PB上，PD∥平面

（1）求证：M是PB的中点；

（2）求二面角B-PD-A的大小；

（3）求直线MC与平面BDP所成角的正弦值.

图2

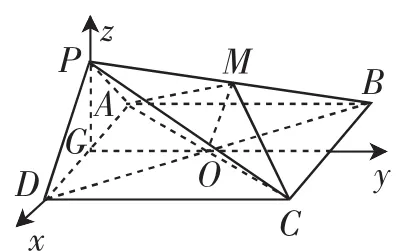
图3

应用分析：直线和平面平行、平面和平面垂直、直线与平面所成角、二面角的平面角都是本题所要考查的知识点.（2）取AD的中点G，可得PG⊥AD，结合面面垂直的性质可得PG⊥平面ABCD，连接OG，则PG⊥OG，再证明OG⊥AD.然后以G为坐标原点，分别以GD、GO、GP所在的直线为x、y、z轴建立空间直角坐标系，求得平面PBD和平面PAD的法向量，根据两个法向量所成角的大小即可得二面角B-PD-A的大小；

解析：（1）略.

（2）取AD的中点G，由PA=PD，得PG⊥AD.又因为平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，PG⊂平面PAD，所以PG⊥平面ABCD.连接OG，则PG⊥OG.由G为AD的中点，O为AC的中点，可得OG∥DC，则OG⊥AD.以G为坐标原点，分别以GD、GO、GP所在的直线为x、y、z轴建立空间直角坐标系，由AB=4，得

设平面PBD的法向量为m=（x，y，z），由

取平面PAD的一个法向量为n=（0，1，0），则cos〈m，故二面角B-PD-A的大小为60°.

教师在教学中应引导学生运用科学的眼光对空间问题进行分析，使学生能够联想到已有的知识与经验，然后对问题进行抽象与转化，使学生在空间向量的辅助下发挥想象并对空间几何体的数量关系进行有效的分析.

四、建构函数模型解决不等式问题

例4若函数f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，且导函数f′（x）的极值点与f（x）的零点相同.

（1）求b关于a的函数关系式，并写出其定义域；

（2）证明：b2＞3a；

（3）假如f（x），f′（x）这两个函数的所有极值之和大于等于求a的取值范围.

解析：（1）先求得导函数的极值点为代入，化简可得由极值的存在条件得a＞3.

（3）求证f（x）的两个极值之和等于0，然后根据根与系数的关系代入并化简可得：导函数的极值不小于，构造差函数，利用导数研究其单调性可得：h（a）在（3，+∞）上单调递减，根据，即可求出a的取值范围为a∈（3，6］.

教学解读：多次构造函数模型是顺利解决本题的关键，由此可见，构造数学模型对培养学生的数学核心素养是正确无误的.

学生的数学运算、逻辑思维、数学分析以及空间直观想象等核心素养与能力在数学模型案例的探析教学中均得到了有意义的锻炼与发展，因此，教师应重视模型构建教学并善于引导学生在这一锻炼过程中获得数学核心素养的发展.W