解析几何问题常见的突破策略

☉新疆实验中学 郑显辉

高考中的解析几何题以圆锥曲线为背景和载体，重点考查圆锥曲线的标准方程、基本性质以及直线和曲线的位置关系.常考题型有：轨迹、最值、定值、对称、参数范围、几何证明、实际应用和探究性问题等.

突破解析几何中的常考题型，需要综合运用“回归定义”“设而不求”“借助平几”“整体代换”“合理引参”“特‘形’引路”等策略，才能简化运算，起到事半功倍的效果.

策略1：回归定义，追根溯源

解决数学问题总离不开相关概念、定义.圆锥曲线的定义既是推导圆锥曲线方程的依据，也是解决圆锥曲线问题的常用方法.若充分使用“回归定义，追根溯源”的策略，把定性的分析与定量的计算有机地结合起来，把比较复杂乃至无从下手的问题转化为比较简单的问题，则可达到准确推理、合理运算、灵活解题的目的.

例1已知圆C：x2+y2+6x-91=0及圆内一点P（3，0），求过点P且与圆C内切的圆的圆心M的轨迹方程.

分析：①两圆内切：外圆半径=内圆半径+圆心距；

②动圆满足等量关系|MC|+|MP|=10＞|PC|；

③由曲线定义得动点的轨迹方程是以P、C为焦点的椭圆；

解：由题意得10-|MC|=|MP|⇒|MC|+|MP|=10＞|PC|=6，

所以所求轨迹是以P、C为焦点的椭圆，

所以2a=10，a=5，2c=6，c=3，b2=a2-c2=52-32=16.

所以圆心M的轨迹方程为

点评：结合圆锥曲线的定义来求动点的轨迹方程，可避免繁琐的计算过程，使解题更加简洁、明快.

策略2：设而不求，多思少算

该策略是指在解题过程中，根据需要设出变量但不直接求出变量的具体值，而是利用和、差、积等某种关系来表示变量间的联系，再结合根与系数的关系、弦长公式、二次函数等得到需要的结论.这种方法在解析几何中有很显著的应用，也是一种重要的解决解析几何问题的途径.比如在解析几何的综合问题中，常常与直线和二次曲线的位置有关，如何避免求交点，从而简化运算，也就成了处理这类问题的难点和关键点.

例2已知椭圆C1的方程为，双曲线C2的左、右焦点分别为C1的左、右顶点，而C2的左、右顶点分别是C1的左、右焦点.

（1）求双曲线C2的方程；

12两个不同的交点，且l与C2的两个交点A和B满足6（其中O为原点），求k的取值范围.

分析：（1）由题意设出椭圆方程，用待定系数法求得方程；

（2）利用“设而不求，多思少算”的策略，根据需要设出变量A、B点的坐标，再利用根与系数的关系表示出变量之间的联系，但不直接计算变量A、B点的坐标值，最后通过运算获得k的取值范围.

解：（1）设双曲线C2的方程为再由a2+b2=c2得b2=1.故双曲线C2的方程为

由直线l与椭圆C1恒有两个不同的交点，得

由直线l与双曲线C2恒有两个不同的交点A、B，得

设A（xA，yA），B（xB，yB），则

故k的取值范围为

点评：本题在求解过程中，利用“设而不求”的策略，使解题过程变得更加简单明了.

策略3：平几渗透，数形结合

解析几何首先是几何问题，在用代数方法研究曲线间关系的同时，若能充分利用图形本身所具有的平面几何性质，则常常可以发现既简便又优美的解法.

例3已知A（3，0）是圆x2+y2=25内的一个定点，以A为直角顶点作Rt△ABC，且点B、C在圆上，试求BC中点M的轨迹方程.

分析：本题若设出圆上动点B、C的坐标，再利用代数方法引入角参数求解，将导致非常复杂的计算.而利用“平几渗透，数形结合”的策略，注意到OM⊥BC（O为原点）（可由“垂径定理”得知），那么再结合∠CAB=90°，|AM|=，即可迅速解题.

图1

解：设M（x，y），如图1，连接OC、OM、MA.

因为M为BC的中点，则由垂径定理知，OM⊥BC，所以

因为在Rt△ABC中

所以|OM|2+|AM|2=|OC|2，即x2+y2+（x-3）2+y2=25.所以点M的轨迹方程为x2+y2-3x-8=0.

点评：本题关注到OM⊥BC（O为原点）这一几何特性，避免了使用动点B、C的坐标来表示M的坐标时所带来的繁杂计算，而直接得到了一个非常明确的结果|OM|2+|AM|2=|OC|2，这样就大大减少了计算量.

策略4：特“形”引路，先知后证

针对解析几何的定点、定值等问题，常常使用该策略，先利用图形的特殊情形、临界状态，由“形”引路得出结论，再证明在一般情形下的结论，就是常说的从特殊到一般的数学思想的运用.

例4已知椭圆的中心为坐标原点O，焦点在x轴上，斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点共线.

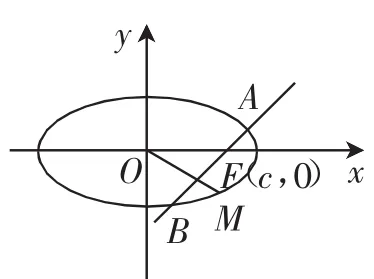
图2

（1）求椭圆的离心率；

（2）设M为椭圆上任意一点，且求证：λ2+μ2为定值.

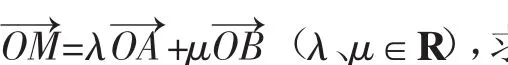
解：（1）易得离心率

由第（1）问的结果，得椭圆方程为x2+3y2=3b2，将点M的坐标代入即得（λx1+μx2）2+3（λy1+μy2）2=3b2，

即λ2（x12+3y12）+μ2（x22+3y22）+2λμ（x1x2+3y1y2）=3b2.

又x12+3y12=3b2，x22+3y22=3b2，

所以

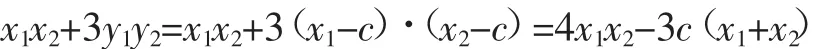
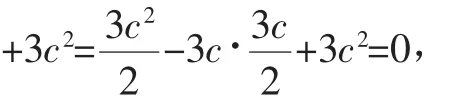
将其代入（*）式，得

故λ2+μ2为定值.

点评：对于（*）这样复杂的式子，学生常常不知所措.而若先通过点M的特殊位置猜出定值，则可以为解题指明方向.

当点M运动到点A时，则λ=1，μ=0，λ2+μ2=1，即可发现定值是1，于是，只要证明x1x2+3y1y2=0即可.

定点、定值问题总会在变化中表现出某些不变量，那么就可以给变化的量赋予特殊的值，从而找到可能的定值或定点，明确情况后，问题便迎刃而解.

综上所述，虽说解析几何在高考试题中处于压轴题的位置，是考生拉开差距的主要考题，一直以来也是大多数考生望而生畏、谈之色变的题型，但我们只要落实基础、掌握方法、加强训练、注重反思总结并利用解题策略，就一定能够突破压轴题的难关.W