基于信息熵和余弦决策的铁路旅客乘车方案排序研究

原方方

（郑州铁路职业技术学院 运输管理学院，河南 郑州 450000)

0 引言

铁路既有线的几次提速以及高速铁路网的逐渐完善，使得选择铁路出行旅客的备选乘车方案大幅增加，对于某个去向的旅客而言，往往具有不同车次的动车组、特快列车、快速列车等多种乘车方案可供选择。剖析旅客乘车行为机理并对其乘车方案选择进行科学的分析，是列车运行计划适应性调整的理论基础，对提高铁路旅客运输服务水平及市场竞争能力具有重要意义。

旅客乘车方案的选择涉及多方面的因素，是一个复杂的系统问题，国内外铁路乘车方案的相关研究多集中于综合运输方式下的旅客出行行为或者不同类型旅客列车偏好。Watson[1］通过构建非集计模型描述城际铁路旅客运输方式选择行为机理。Wilson等[2］亦以非集计理论量化分析出行时间及费用因素对旅客选择行为的影响。史峰等[3］采用效用理论量化分析旅客乘车行为，并根据收入状况划分旅客群体并计算其对各类列车的选择概率。江南等[4］通过定义顺序拆分径路及运算符，构建多目标铁路旅客乘车方案优化模型。杨信丰等[5］利用信息熵法确定旅客乘车选择各目标的权重，设计各出行可行路径的快速搜索算法及综合效用值。王文宪等[6］构建多元Logit模型分析不同类型旅客对不同类型高速列车的选择行为机理。

上述研究为铁路旅客乘车方案评价研究奠定了理论基础，通过对铁路旅客乘车方案影响因素进行系统分析，筛选铁路旅客乘车方案评价指标，运用信息熵理论确定各评价指标的权值，在此基础上定义了铁路旅客乘车方案的指标线段、理想指标线段以及指标线段夹角等，并通过比较其加权余弦值大小的综合评价方法对乘车方案进行优劣排序，期望为列车运行方案的适应性调整提供理论依据。

1 铁路旅客乘车方案评价指标

通过相关文献的检索，铁路旅客乘车方案影响因素主要包括出行费用消耗、出行时间消耗、出行方便度、出行疲劳度以及出行时间满意度[7］，这几个影响因素作为评价指标，对铁路旅客乘车方案进行评价及比选。

（1）出行费用消耗U1。旅客出行费用消耗因列车等级不同而具有较大差异，我国铁路列车包括动车组、直达特快、特快列车、快速列车及普通列车等。根据12306客票系统，铁路线路上两站点间的列车票价均可以查询得到，研究中以各类列车的最低票价进行计算(如二等座为动车票价、硬座为特快列车票价)，旅客乘坐k次列车从i站到j站的列车票价记为cij(k)。

（2）出行时间消耗U2。旅客出行时间消耗包括2个部分：列车运行时间及换乘候车时间。

①列车运行时间影响因素包括列车的运行里程，以及所选列车类型，旅客乘坐k次列车从i站到j站所用的乘车时间(k)为

式中：(k)为k次列车到达j站的时刻；(k)为k次列车从i站出发的时刻。

②换乘候车时间为旅客在h站由k1次列车换乘至k2次列车的等候时间，即k2次列车在h站的出发时刻与k1列车在h站的到达时刻时间差，若两者差值小于一个紧接续标准(一般取值为t0=20 min)，则时间差应增加/d，即1 440 min，其计算公式为

综上，出行时间消耗为

（3）出行方便度U3。旅客出行方便度为旅客自起点出发到达目的地过程中换乘列车的次数，由于中转换乘耗时耗力，换乘旅客在途疲劳程度高且出行过程繁琐，因而对于旅客而言，一般情况下不会选择换乘次数过多的乘车方案，设置最大换乘次数为= 1。

（4）出行疲劳度 。引用文献[5］的研究成果，将旅客出行疲劳度定义为旅客乘坐列车后的疲劳恢复时间，该时间与列车运行时间及列车类型相关，旅客乘坐k次列车从i站到j站的疲劳恢复时间计算公式为

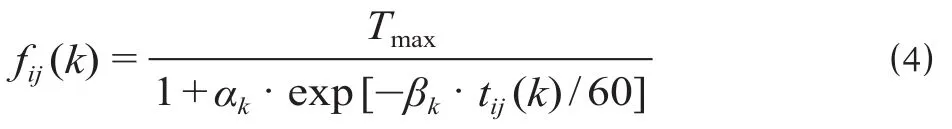
式中：Tmax表示疲劳恢复时间上限，通常取值为14 ～ 15 h；参数αk与βk为乘车疲劳恢复时间强度系数，参数αk，βk取值如表1所示。

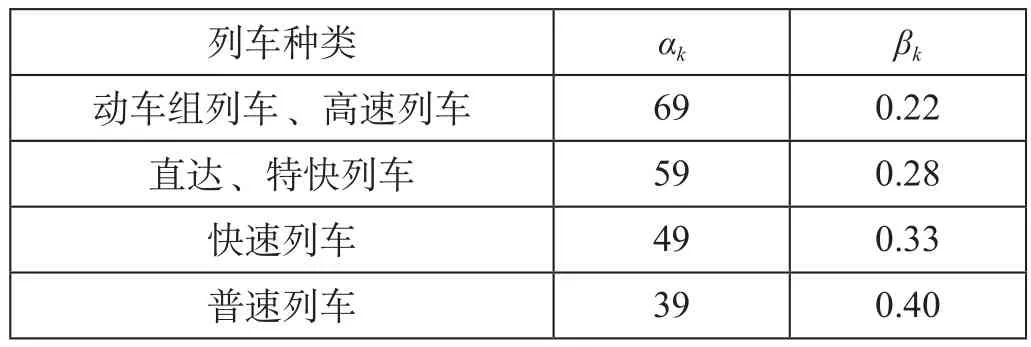
表1 参数αk，βk取值Tab.1 Value of the parameter αk, βk

（5）出发时间满意度U5。出发时间满意度[8］是指铁路旅客乘车方案中列车始发时间对于旅客的方便程度。为确定不同发车时间对于旅客的方便度，以30 min为间隔将0 : 00—24 : 00分为48个发车时间段，基于问卷调查的形式让旅客根据自己的偏好选择其最满意的发车时间段，数据统计结果可以发现，旅客对发车时段偏好出现2个高峰，第1个高峰在9 : 00—11 : 00间，第2个高峰在16 : 00—17 : 00间，该数值表明了旅客对各发车时段的偏好程度 。不同发车时段对旅客的方便程度如图1所示。

图1 不同发车时段对旅客的方便程度Fig.1 Convenience to passengers at different departure times

2 基于信息熵和余弦决策的旅客乘车方案排序模型构建

现有评价指标权重的确定方法多为主观确定权重法，诸如专家打分、AHP等，但上述方法难以避免人为干扰导致的结果偏差。而采用信息熵对评价指标在较大程度上缓解指标权重计算中主观因素，从而使评价结果更近于实际。余弦决策主要通过定义指标线段和理想指标线段，然后比较备选乘车方案与理想方案之间的指标线段加权余弦值来确定铁路旅客乘车的最佳决策方案，加权余弦值越大表示备选乘车方案越接近理想乘车方案，即备选乘车方案越优。假设某去向铁路出行旅客有n个可供选择的乘车方案作为方案备选集，记为A= {A1，A2，…，An}，以上述乘车方案评价指标作为指标集，记G= {G1，G2，…，Gm}。乘车方案Ai对指标Gj的属性值为yij，矩阵Y= (yij)n×m为方案集A对指标集G的决策矩阵。

2.1 指标权重确定

根据评价指标值判断矩阵对各铁路乘车方案评价指标的权重进行计算，其步骤如下。

步骤1：在原始数据矩阵中，由于各乘车方案评价指标的含义和计算方法不同，造成它们的量纲各异，而且U1，U2，U4的期望值越小越优，即为“极小极优型”指标，U5的期望值越大越优，即为“极大极优型”指标，故先采用关联函数对上述指标函数计算值进行标准化处理。

（1）对“极大极优型”指标，计算公式为

（2）对“极小极优型”指标，计算公式为

式中：rij为第i个乘车方案在第j个评价指标的标准值。

步骤2：定义评价指标的熵，第j个评价指标的熵值计算公式为

式中： 为一常数，其取值为η= (lnn)-1；fij为第j个评价指标上在第i个乘车方案所占的比重，fij=rij/

步骤3：计算评价指标的权重，第j个指标的熵权ωj计算公式为

2.2 评价模型构建

令铁路旅客理想乘车方案为A*= (g1，g2，…，gm)，其中…，m，各备选乘车方案为Ai= (ri1，ri2，…，rim)。令它们在二维空间xoy中对应的点分别为(a1，a2，…，am)和(ai1，ai2，…，aim)，则有

定义1：乘车方案的指标线段是指二维空间xoy中，以原点o为起点，以乘车方案Ai在指标Gj的值rij为终点aij，构成的有向线段oaij。

定义2：理想乘车方案的指标线段是指二维空间xoy中，以原点o为起点，以理想乘车方案A*的指标值gj为终点aj，构成的有向线段oaj(j= 1，2，…，m)。

定义3：备选乘车方案Ai的线段夹角是指二维空间xoy中，理想乘车方案指标线段oaj与备选乘车方案Ai的指标线段oaij之间的夹角(夹角为锐角 )θij。

各指标线段定义示意图如图2所示。

图2 各指标线段定义示意图Fig.2 Schematic diagram of each indicator line segment definition

依据定义，理想乘车方案指标线段集合为{oa1，oa2，…，oam}，各备选乘车方案的指标线段集合为 {oai1，oai2，…，oaim}，i= 1，2，…，n。

理想乘车方案指标线段oaj和备选乘车方案指标线段oaij的夹角为θij，则

于是得到铁路旅客乘车方案Ai与理想乘车方案A*之间的夹角余弦值。确定夹角余弦值cosθij后，与熵权ωj相乘求和即可得到加权余弦值Di：

夹角余弦值cosθij随夹角θij的增大而减小，因而cosθij越大表示乘车方案Ai在指标Gj下的值rij与理想方案A*的指标值gj越接近。因此，依据公式 ⑽，加权余弦值Di的值越大表示备选乘车方案Ai越接近理想乘车方案A*，即备选乘车方案Ai越优。

2.3 排序模型算法步骤

步骤1：乘车方案筛选。对任意某个去向的出行需求od而言，利用铁路客运服务系统列车时刻表，可在短时间内得到多个该去向的备选列车乘车方案以供选优，令经过o站及d站的列车集合Lo与Ld。①直达乘车方案：搜索列车集合Lo与Ld的交集Li=Lo∩Ld，进行以下判定，如果列车Li∈Li在o站的出发时刻(li)早于在d站的到达时刻(li)，即(li) ＜(li)，则表示列车li为从o站到d站的直达乘车方案。②一次换乘乘车方案：分别搜索只经过o站与d站的列车集合Lm=Lo-Ld与Lk=Ld-Lo，若换乘站vt∈Vlm∩Vlk且(lk)，则表示从o站乘坐列车lm在车站vt可换乘列车lk到达d站，从而得到一次换乘乘车方案。

步骤2：建立决策矩阵。依据铁路旅客乘车方案的评价指标函数式 ⑴—⑷，建立乘车方案集的初始决策矩阵Y= (yij)n×m。

步骤3：决策矩阵标准化处理。对初始乘车方案决策矩阵做标准化处理，得到标准决策矩阵R=(rij)n×m。

步骤4：计算乘车方案的线段夹角。依据定义1、定义2、定义3和公式 ⑼，计算各乘车方案的线段夹角余弦值 cosθij。

步骤5：计算乘车方案各指标的权重值。依据公式 ⑸ 至公式 ⑻，得到各指标的权重值ωj(j= 1，2，…，m)。

步骤6：确定决策方案加权余弦值。根据公式⑽ 计算各备选乘车方案的加权余弦值Di，并依据各加权余弦值Di的大小对乘车方案进行排序，加权余弦值Di越大代表其对应的乘车方案Ai越优。

3 案例分析

利用2018年5月的铁路旅客列车时刻表，首先筛选兰州至太原的铁路旅客乘车方案，根据国家高速铁路网示意图选取途中的西安北站为换乘站点，最大换乘次数为1，换乘最小时间消耗15 min，最大换乘等待时间为1 h，得到可选乘车方案13种，其中，直达乘车方案3种，换乘乘车方案10种。旅客备选乘车方案评价如表2所示。

表2 旅客备选乘车方案评价表Tab.2 Passenger travel plan evaluation form

（1）理想对象的确定。由前文分析，铁路旅客乘车方案评价指标包括：出行费用消耗U1、出行时间消耗U2、出行方便度U3、出行疲劳度U4以及出行时间满意度U5。上述13种乘车方案中，由于各乘车方案票价一致，故将出行费用消耗U1略去。根据剩下的乘车方案评价指标最优值的筛选，可确定理想乘车方案参考数列Y0= {382，0，0.749，0.144}，包含理想方案与各备选乘车方案的指标序列为

（2）原始数据的无量纲化处理。根据公式 ⑴至公式 ⑷，旅客乘车方案的原始数据无量纲化处理后的结果为

（3）指标权重确定及方案排序。根据公式 ⑸ 至公式 ⑻，各评价指标权重系数为ω2= 0.24，ω3= 0.22，ω4= 0.18，ω5= 0.36。由公式 ⑼ 至公式 ⑽，各乘车方案Ai与理想乘车方案A*之间的加权余弦值如表3所示。

表3 各乘车方案与理想方案的加权余弦值Tab.3 Weighted cosine of each ride and ideal plan

根据判断准则，各乘车方案的综合优劣排序为：方案(10) ＞方案(7) ＞方案(3) ＞方案(12) ＞方案 (11) ＞ 方案 (2) ＞ 方案 (13) ＞ 方案 (1) ＞ 方案 (5) ＞方案(4) ＞方案(9) ＞方案(6) ＞方案(8)。排名前三的乘车方案为：D2692/D2530、D2660/D2524、D2570。其中，乘车方案(10)与(7)为换乘方案，乘车方案(3)为直达方案。

（4）结果分析。可以看出，对于选择高速铁路出行的旅客，3种无换乘直达乘车方案综合评价值排名分别为第3、第6、第8，说明高速铁路成网条件下，由于换乘站点及换乘列车等便利条件的存在，直达乘车方案对于旅客并不像既有铁路那般具有吸引力。当换乘次数指标权重ω3分别取值0.25，0.30，0.35，0.40时，在其他指标权重相对值不变条件下，不同换乘次数权重下的各乘车方案加权余弦值如表4所示。

可以看出，随着换乘次数指标权重值的提高，D2566、D2568及D2570等直达方案在整体上排名有所提升，但排名第一、第二的方案依然为D2692/D2530、D2660/D2524 这2种换乘方案。这种现象也为我国高速铁路成网条件下，逐步减少长途跨线高速列车开行数量、改变为中短途换乘运输模式提供理论依据。

表4 不同换乘次数权重下的各乘车方案加权余弦值Tab.4 Weighted cosine of each ride plan scheme under the weight of different transfer times

4 结束语

根据我国铁路实际对铁路旅客对乘车方案的排序方式进行研究，确立了评价指标体系，并通过信息熵和余弦决策理论得到各评价指标的权重和各备选方案的加权余弦值，确定备选方案的排序，这也是铁路客运研究的核心和趋势。实例研究结果表明，在高速铁路成网条件下，旅客对于直达乘车方案的偏好较弱，对列车开行时段具有较高的需求，为铁路运营管理部门制订、调整和优化旅客列车开行方案提供参考，进一步提高旅客服务质量。该决策模型较大程度上避免了人工决策的主观性，并且计算简单、使用方便。