对一道思考题的探究
康玉清 刘艳艳
一年级学生处于知识的启蒙阶段,其思维以形象思维为主。从整体上看,一年级学生思维都比较活跃,但大部分学生都不知道如何思考问题。因此,笔者认为,从小学一年级开始,培养学生的思维方式特别重要。我们在教学中可以借助一些发散性思考题,培养学生的思维。
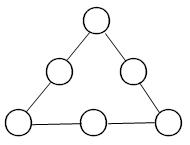
在人教版数学教材一年级上册中有一道这样的思考题:请将1、2、3、4、5、6这六个数填入“○”中,使图中每一行的三个数相加的和都是9。
小学一年级上学期的数学知识主要是掌握20以内的加减及其运用,学生对这种思考题的理解有一定的困难。此时,引导学生怎样分析与思考显得十分重要。教师可利用这种类型的思考题,引导学生加强对数学概念的理解,以便系统地掌握数学学习的方法,形成数学思维方式。
解析这道题,我们可以这样引导学生思考:这六个数的和为1+2+3+4+5+6=21;而三角形三边的和为9+9+9=27;所以此时三角形三个顶点的数之和为27-21=6。而1、2、3、4、5、6这六个数中,1+2+3=6,即三个顶点的数分别是1、2、3,所以中间三个数依次为:9-1-2=6,9-1-3=5,9-2-3=4。
笔者在教学这道思考题时,发现将1、2、3、4、5、6这六个数填入“○”中,图中每一行的三个数相加之和不仅可以是9,还可以是10、11和12。
我们先看每一行的三个数之和为12的解题思路,这与每一行的三个数之和为9的思路一样。此时三角形三边的和为12+12+12=36,三角形三个顶点的数之和为36-21=15。在1、2、3、4、5、6这六个数中,4+5+6=15,即三个顶点的数分别为4、5、6,故中间三个数依次为:12-4-5=3,12-4-6=2,12-5-6=1。
在解答每一行的三个数之和为10与11时,我们首先必须告诉学生单、双数的概念,然后引导学生弄清楚:单数+单数=双数,双数+双数=双数,单数+双数=单数。
有了单、双数知识的准备,解决每一行的三个数之和为10与11就比较简单了。根据上面的解题思路,当每一行的三个数之和为10时,三角形三边的和为10+10+10=30,三角形三个顶点的数之和为30-21=9。在1、2、3、4、5、6这六个数中,和为9的三个数比较多,但因为9是单数,我们引入单数+单数+单数=单数;同时因三角形每一边三个数的和为10,10为双数,单数+双数+单数=双数,可知此时三个顶点对应的数均应为单数。而在1、2、3、4、5、6这六个数中,1+3+5=9,即三个顶点的数分别为1、3、5,则中间三个数依次为:10-1-3=6,10-1-5=4,10-3-5=2。
当每一行的三个数之和为11时,三角形三边的和为11+11+11=33,三个顶点的数之和为33-21=12。同样地,在1、2、3、4、5、6这六个数中,和为12的三个数比较多,但因为12为双数,我们就可以引入双数+双数+双数=双数;同时因三角形每一边三个数的和为11,而11为单数,双数+单数+双数=单数,可知此时三个顶点对应的数均应为双数。在1、2、3、4、5、6这六个数中,2+4+6=12,即三个顶点的数分别为2、4、6,则中间三个数依次为:11-2-4=5,11-2-6=3,11-4-6=1。
同时,笔者在以上题目的基础上,经过推演、验算,得出结论:只要是构成等差数列的六个数填入上述题中的六个圆内,均可按以上解题方式求解。
叶圣陶先生曾说“教是为了不教”,也就是说,我们教学的主要目的是“授人以漁”。从小学一年级开始,我们注重对学生思维方式的培养,能帮助学生更好地在数学乐园中自由地探索,感受数学学习的乐趣。
(作者单位:新化县温塘镇枫树完小)

