凹坑-树状分叉微细通道换热特性的数值研究

税琳棋， 孙建辉， 高 峰， 吴文武

(1.西安理工大学教育部数控机床及机械制造装备集成重点实验室，陕西西安710048； 2.西安理工大学陕西省制造装备重点实验室，陕西西安710048)

重型燃气轮机是构成先进能源动力循环系统的核心装备，其功率输出和循环热效率均随着透平初温的提高而增加。目前先进燃机透平的进口初温已达到1900 K，这已远远超过叶片材料所能承受的温度极限。为了保证叶片在高温下的安全运行，必须对其采取有效的冷却措施[1]。先进叶片冷却技术的研究方向包括对叶片结构参数和复合冷却方式的优化与改进，发展基于新思想、新理论的新型冷却技术以及采用新型冷却介质替代原有空气冷却等[2]。其中，基于涡流强化传热机理的表面凹坑换热技术和基于微尺度强化传热机理的树状分叉微细通道换热技术均是极具竞争力且富有前景的冷却技术。

凹坑结构在通道中产生的强烈而有序的涡旋，会在近壁面区域引起气流的分离和重附着，从而有效地强化传热[3]。Ligrani和Mahmood等[4]，Murata等[5]和Xie等[6]分别对带凹坑的直通道或蛇形弯曲通道中的强化传热与流动特性进行研究。他们发现与光滑通道相比，凹坑通道的强化传热性能提高大约2至3倍，而流动阻力并没有明显的增加；与带肋通道相比，凹坑通道强化传热性能与其相当，压力损失却仅有其一半左右。由于透平叶片内部结构十分复杂，研究者往往将凹坑换热结构与其它冷却方式灵活结合，从而获得更好的冷却效果。Kanokjaruvijit等[7]以凹坑表面作为冲击靶面进行传热实验，以期更好的对叶片前缘等高热负荷区域进行冷却。Shen等[8]采用数值方法研究了叶片尾缘区域存在凹坑与射流劈缝复合冷却结构时的复杂流动与换热特性。他们的研究表明，在叶片中采用带凹坑的复合强化传热结构，能够在不明显增加流动损失的情况下，有效提高叶片内部的冷却效果。

树状分叉微通道网络是自然界中非常普遍的结构，具有生物系统特有的高效质量和能量输运特性。近年来，受自然分叉网络系统的启发，树状分叉网络在工程领域的应用被不断实现和拓广[9]。Bejan[10]最早讨论了树状分叉微细通道在微电子冷却方面的应用，采用构造理论设计的冷却网络在减小压降的同时提高了冷却的均匀性。Chen等[11]研究了树状分形分叉微通道在对流换热过程中的热流量和压降分布，发现分叉网络可以在增大流道总热流量的同时减小压降，具有更高的热效率。Senn和Poulikakos[12]发现分叉结构的优势在于既可以使通道中逐渐降低的压力得到恢复，又能够使流动边界层发生破坏，产生二次流涡流加剧流体的相互掺混，从而提高当地换热系数水平。孙纪宁等[13]对透平叶片微细冷却通道中的换热特性进行研究，发现当微细通道存在分叉结构时叶片综合冷却效果更好。西门子公司的Ahmad等[14]设计了一种带树状分叉结构的透平叶片，并认为这种分叉结构可以在叶片内部发生损坏或堵塞时，有效维持整体叶片的冷却效果。Shui等[15, 16]针对叶片内部树状分形微通道的流动和换热特性进行了一系列的实验和数值研究，发现在高雷诺数下的分叉微通道具有更加优越的流阻-换热特性。

虽然目前已有不少学者对凹坑强化换热技术和树状分叉微细通道强化换热技术分别进行了深入研究，但将两种结构进行有机结合从而进一步提高透平叶片冷却效果的尝试尚未见诸公开报道。将凹坑结构与树状分叉结构进行复合，得到的新型冷却结构不仅拥有更为良好的流阻-换热特性，并且还具有管径尺寸小、管道分支设计灵活的特点。将这种新型结构应用在承受复杂热负荷工况的透平叶片里，可以根据叶片表面的热负荷分布特点去调整冷却通道的布置方案，使高热负荷区域获得更强的冷却效果，从而优化叶片表面的温度分布，有效减小温度梯度和热应力，因此极具应用潜力。

本文利用Shui等实验所使用的T型树状分叉微细通道结构[16]作为原型，在其上壁面处布置一系列凹坑从而设计出凹坑-树状分叉微细通道复合换热结构，并采用数值模拟方法探索雷诺数和工质性质变化对其流动和换热特性的影响规律，以及蒸汽冷却下不同凹坑流向间距(s/D)对通道强化换热特性的影响，得到的研究结果可以为叶片高效冷却的优化设计提供借鉴和参考。

1 计算模型和数值方法

图1给出了T型树状分叉微细通道的几何示意图，其边界条件设定与前述实验保持一致。为了全面而深入地研究凹坑结构对树状分叉微细通道中的流动和换热特性的影响，在本文的数值模拟中设计了三种不同的凹坑布置方案，其细节如图2所示。通道中所有凹坑的形状均为球形，投影直径D=0.7 mm，深度e=0.14 mm。在三种布置方案里，凹坑沿流向的布置间距s分别为2.1 mm、4.2 mm和6.3 mm，即无量纲流向间距比s/D分别为3、6和9，凹坑的总横截面积分别占通道上壁面面积的14.0%、6.7%和4.7%。

计算网格采用ANSYS ICEM CFD软件生成，图3给出s/D=3时的通道网格图。计算采用分块结构化网格，并进行近壁面区域的局部加密处理，使主要换热壁面的y+值小于1。为保证计算的准确性，本文对网格无关性进行了验证。结果发现，对光滑树状分叉微细通道而言，当网格节点数增大到9.72×106后，计算结果已对网格数不敏感；对于三种带凹坑的微细通道，合适的网格节点数则分别为1.998×107、1.893×107和1.869×107。

在ANSYS CFX软件中，利用全隐式求解器求解三维不可压缩稳态雷诺时均方程，计算精度选择高精度格式。计算中，空气的热力学性质采用理想气体模型进行描述，蒸汽的热力学性质使用IAPWS-IF97标准进行计算。进口边界条件给定冷气的平均质量流量、静温和湍流度；出口边界条件给定冷气的静压；底部加热壁面设为定常热流密度，其余壁面给定绝热边界条件，所有壁面均设为无滑移边界。SSG雷诺应力模型对于通道中的复杂流动与换热情况具有较好的预测精度，因此本文采用该湍流模型进行数值计算。作者在已有研究中[16]验证了该模型对树状分叉微细通道的流动传热过程模拟的合理性。

图2 凹坑布置方案Fig.2 Geometrical layout of the dimples

图3 凹坑-树状分叉微细通道计算网格Fig.3 Grid in computational domain

为了便于对比，本文采用通道进口参数定义雷诺数Re：

(1)

式中，ρ为冷气的密度；μ为冷气的动力粘度；din为通道进口处的水力直径；uin为通道进口处的冷气平均速度，通过对该处的冷气质量流量进行计算得到。

通道带凹坑侧壁面的换热系数用努塞尔数Nu表示：

(2)

式中，λ为冷气的导热系数；q为通过通道壁面的热流密度；Tw为通道壁面温度；Tb为通道中冷气的局部体积平均温度。

定义通道的摩擦系数f为：

(3)

2 结果分析与讨论

2.1 蒸汽与空气换热特性比较

通道中流体的换热特性与其流场结构紧密相关。当通道中存在二次流流动时，流体的湍流度将增大，流体微团的混合程度会得到强化，从而使通道的换热水平得到增强。涡旋核心是一种由临界点理论发展而来的可以用于显示涡旋结构和分布的拓扑可视化技术，能够清晰明确地显示流场中不同强度的涡旋的分布规律、形状和大小[17]。借助涡旋核心技术，可以对复杂通道中的二次流进行完整的显示，从而实现对二次流动的强化传热机理的深入研究。图4显示了当进口质量流量为2.45×10-4kg/s，即蒸汽的Re数为5 400时，蒸汽和空气在凹坑-树状分叉微细通道中的二次流涡旋核心分布规律。由图可见，相比于光滑通道，凹坑通道中产生的二次流涡旋不仅包括了由分叉结构诱导形成的纵向二次流涡旋，还存在由凹坑结构引起的二次流涡旋阵列，这使得凹坑-树状分叉微细通道中的流动更加复杂。对蒸汽和空气的流动特性进行比较，可以发现，两者的二次流涡旋分布特征非常相似。但是由于蒸汽的密度小于空气，在相同的质量流量下，蒸汽的流速更高，从而使得涡旋的强度更大，流体微团中间的质量和能量交换更剧烈。

图4 蒸汽和空气在凹坑与光滑树状分叉微细通道中的涡旋核心分布Fig.4 Contour plot of turbulence kinetic energy in the vortex core region of the branching micro- channel with steam and air flow

如图5(a)所示，L1至L4分别为树状分叉微细通道各级子通道壁面的中心线，图5(b)～(e)显示了在凹坑-树状分叉微细通道中分别以蒸汽和空气作为冷却工质时的换热系数h沿流动方向无量纲距离z/L的变化规律。

图5 蒸汽和空气在凹坑与光滑树状分叉微细通道中的当地换热系数分布Fig.5 Local heat transfer coefficient distribution of steam and air flow in the branching microchannel with and without dimples

为了方便对比，图中同时给出光滑树状分叉微细通道中两种冷却工质的当地换热系数的变化情况。可以看出，与光滑通道相比，凹坑通道的换热系数呈现周期性波动并具有显著提升。蒸汽冷却通道中L1至L4的换热系数水平分别提高了26.7%、14.6%、22.2%和25.9%，而空气冷却通道中各级子通道中心线上的换热系数分别提高了26.5%、14.3%、25.0%和32.6%。这是由于在凹坑-树状分叉微细通道中，不仅存在由通道分叉所引起的二次流纵向涡旋传热强化，还存在凹坑诱导形成的三维流动和不同尺度的涡旋所引起的壁面传热强化。同时，蒸汽冷却的换热效果要优于空气冷却，这是由于一方面蒸汽的热物理性质优于空气，具有更高的普朗特数Pr，即蒸汽的热边界层较薄，换热效果更好；另一方面蒸汽在通道中的二次流涡旋强度更强，也将引起更为强烈的热量交换。

图6对不同Re数下的蒸汽和空气的平均换热性能进行了比较。其中，Nus和Nua分别为蒸汽和空气的平均努塞尔数。从图中可见，在凹坑-树状分叉微细通道中，蒸汽的Nu数比空气的高约48%至67%，而在光滑树状分叉微细通道中，蒸汽的平均换热性能比空气高约56%至68%。虽然凹坑-树状分叉微细通道中蒸汽的换热优势低于光滑树状分叉微细通道，但两者数值相差并不大。这说明蒸汽相比于空气的换热优势主要取决于它们的热物理属性，而通道结构和Re数的变化对其影响较小。

图6 不同Re数下蒸汽与空气的Nu数比变化趋势Fig.6 Nu number ratio of steam and air flow with different Re number

2.2 蒸汽强化换热性能分析

本节研究无量纲流向间距比s/D分别为3、6和9时的蒸汽强化换热特性的变化规律，Re数的变化范围为3 000至90 000。如图7所示，相对于光滑树状分叉微细通道，凹坑-树状分叉微细通道中蒸汽的无量纲换热系数增强程度可以用Nus,d/Nus,s来表示。

从图中可见，三种s/D下的Nus,d/Nus,s均随着Re数的增加而逐渐减小。当Re数的变化范围为3 000到10 000时，三条曲线的下降斜率较大，换热系数比值迅速减小；而随着Re数的继续增大，曲线的斜率均变小，换热系数比的减小趋势逐渐放缓。当Re=3 000时，s/D取3、6和9时的Nus,d/Nus,s值分别为1.55、1.40和1.38；当Re=90 000时，Nus,d/Nus,s值则分别降为1.10、1.02和1.01。这说明随着Re数的增加，湍流状态下的主流扰动加剧，流体间的相互掺混使得换热得到显著加强，而凹坑结构的换热强化作用则被削弱。

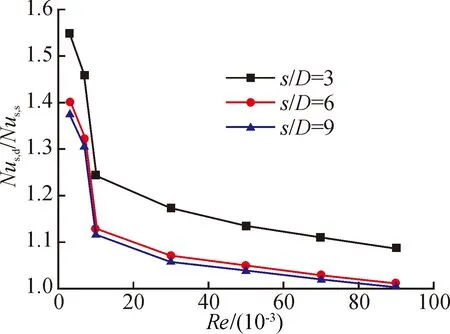
图7 不同Re数下蒸汽的Nus,d/Nus,s变化趋势Fig.7 Nus,d/Nus,s of steam flow with different Re number

如图8所示，相对于光滑树状分叉微细通道，凹坑-树状分叉微细通道中蒸汽的无量纲摩擦系数增强程度可以用fs,d/fs,s进行表示。从图中可以发现，随着Re数从3 000增大到30 000，三种s/D下的fs,d/fs,s均呈现出迅速增加而后减小的趋势，在Re=3 000时，s/D为6和9的曲线获得最小fs,d/fs,s值分别为1.08和1.01，而s/D=3的曲线在Re=30 000时获得最小fs,d/fs,s值为1.17。然后随着Re数的增加，三条曲线的数值均开始逐渐增大。这说明随着Re数的增加，凹坑结构带来的阻力损失在逐渐增大。

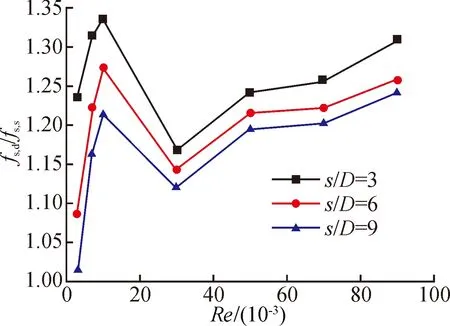
图8 不同Re数下蒸汽的fs,d/fs,s变化趋势Fig.8 fs,d/fs,s of steam flow with different Re number

在通道中，冷气的换热系数增加的同时，不可避免地会产生更大的摩擦阻力损失。因此，往往采用强化换热因子η=(Nus,d/Nus,s)/(fs,d/fs,s)1/3来全面评价通道的强化换热性能。图9显示了不同Re数下的蒸汽强化换热因子的变化规律。从图中可见，三种s/D下的η值均随着Re数的增大而逐渐减小。当s/D=3时，蒸汽的η值最大，其变化范围为1.44～1.01；随着s/D从6增加到9，η值略有减小，但总体而言变化并不明显。

图9 不同Re数下蒸汽的η变化趋势Fig.9 η of steam flow with different Re number

3 结 论

本文采用求解三维稳态雷诺时均N-S方程和SSG雷诺应力模型的方法，数值研究了凹坑-树状分叉微细通道中蒸汽和空气的流动与换热特性，并与光滑树状分叉微细通道中的计算结果进行比较，分析了凹坑流向间距变化对蒸汽冷却强化换热特性的影响，在所研究的Re数范围内可以得到几点结论。

1) 蒸汽和空气在凹坑-树状分叉微细通道中的流场特征十分相似，均主要包括分叉结构产生的纵向涡二次流以及凹坑结构引发的分离涡二次流。在相同的进口质量流量下，蒸汽的涡旋强度高于空气，使得通道中的蒸汽冷却具有更强烈的热交换。

2) 在凹坑-树状分叉微细通道中，蒸汽的平均Nu数是空气的1.48～1.67倍。蒸汽相对于空气的换热优势主要受气体的热物理性质影响，通道结构与Re数的变化对其影响较小。

3) 在三种凹坑流向间距下，通道中蒸汽的Nus,d/Nus,s和η均随着Re数的增加而逐渐减小，fs,d/fs,s则随着Re数的增加先增大再减小，而后继续增大。当s/D=3时，通道中的蒸汽冷却获得最佳的强化换热性能。