拱坝基础垫座体形优化模型研究

娄靖雪，卢晓春，熊勃勃，陈博夫，张 鑫

(三峡大学水利与环境学院，湖北 宜昌 443002)

0 引 言

在拱坝设计中常遇到复杂的地形条件，其中深“V”形峡谷地形对坝体的不利影响尤为突出，为此常在拱坝坝基处设置人工垫座以改善坝体的应力状态[1]。在建造垫座时，首先需要按照垫座几何尺寸开挖基岩，再回填混凝土。在保证坝体安全的前提下，优化垫座的几何尺寸，能有效降低基岩的开挖工作量及混凝土用量，具有重要的工程意义。

针对上述问题，冯继军[2]对垫座开挖方式以及垫座结构进行调整，对比分析了不同坝体上游垫座长度对坝体的影响；潘元炜[3]通过调整垫座宽度尺寸，对将垫座视为基础或坝体两种思路进行比较，得到了最优的垫座设计方案；陈渴鑫[4]研究了3种垫座设计方案，分别得到了不同弹性模量以及垫座高度对坝体应力的影响规律。上述研究通过对比分析垫座方案对坝体应力状态的影响，对垫座参数进行优化，但对多个垫座体形参数的综合作用研究甚少。

本文选取垫座高度、厚度、垫座底面圆心角等3个体形参数，确定了垫座优化设计中的约束方程以及目标函数，从而建立了基于有限元等效应力法的垫座体形优化模型，以某实际工程为例，运用此模型求出任一高度面垫座体形最优点，再综合考虑最优点间的体积关系，确定垫座最优尺寸，为工程提供参考。

1 垫座优化模型

垫座体形优化设计的数学含义即指在给定条件下，综合考虑垫座相关体形参数，求出满足约束条件并使目标函数值最小的设计变量解[5]。建立垫座体形优化的数学模型主要包括选定设计变量、确定目标函数以及建立约束方程三部分内容。

设计变量即指用于确定垫座几何形状特性的可变量，本文选用垫座的高度、厚度、底面圆弧所对应的圆心角度数作为垫座体形优化模型的三个参数。垫座的几何特征示意如图1所示。

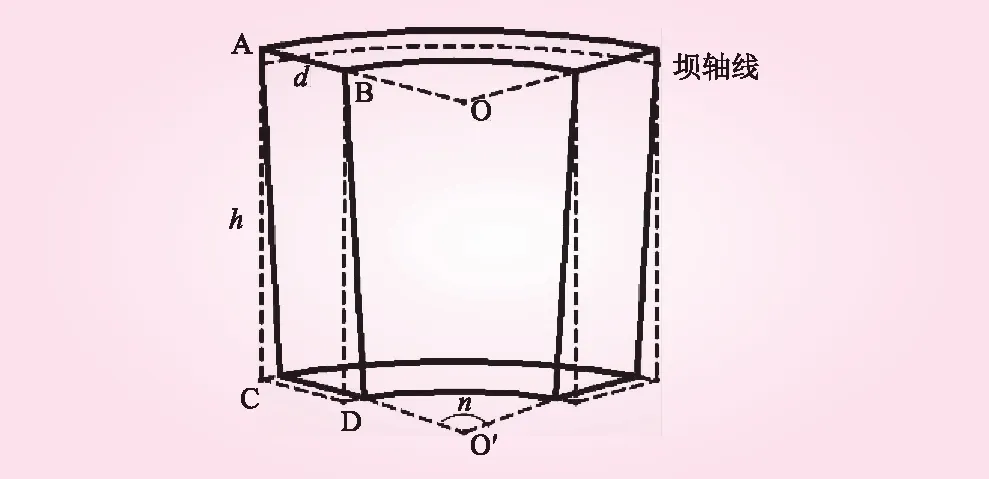
图1 垫座的几何特征示意

现有的垫座优化设计大多是以单目标优化为主，根据工程需求，将坝体或垫座应力最小作为目标[2-3]，最优垫座体形需综合考虑垫座对拱坝的影响，兼顾考虑垫座的安全性和经济性。由于垫座体积增大直接影响开挖量与混凝土用量，所需费用较高，为了达到经济最优，本文将垫座体积视为目标函数。

设置垫座是为了改善坝体的受力条件，故选择坝体最大拉应力及最大压应力作为约束条件。拱坝应力常采用有限单元法进行计算，可能因应力集中，结果可靠性较差。为此，朱伯芳、傅作新等学者曾提出有限元等效应力法[6-7]来计算坝体应力。为精确考虑应力的影响，本文通过Fortran编程，对有限元计算结果进行处理，将坝体的等效应力引入三参数模型，作进一步的分析。并采用单纯形法对该模型进行求解，优化问题即可归结为：

求h，d，n，使V(h，d，n)→min

(1)

式中，V(h，d，n)为垫座体积；h、d、n分别为垫座高度、厚度、底面圆心角度数；hmin、hmax分别为垫座高度上下限取值；dmin、dmax分别为垫座厚度上下限取值；nmin、nmax分别为垫座底面圆心角上下限取值；σtmax为坝体最大等效拉应力；σcmax为坝体最大等效压应力；[σt]为坝体允许拉应力；[σc]为坝体允许压应力。

2 应用研究

2.1 基本工况

某大坝为混凝土双曲拱坝，坝顶高程655.50 m，最大坝高62.50 m，总库容581.43万m3，工程属四等小(1)型水库。流域内河床狭窄，坝址为深“V”形峡谷，两岸山坡陡峻。因河谷地形限制，坝基处无法形成拱圈，所以在该处进行了混凝土基础回填，并在底部设置垫座来改善坝体的应力、位移分布及稳定条件。垫座顶部宽12.5 m，顶部轮廓为扇形面，中心角与拱坝坝基拱圈中心角一致，为84°，上下游圆弧半径分别为32.5、16 m。

为研究坝体的3个体形参数对坝体应力的影响，寻求在满足约束条件下的最优垫座体积，本次计算分别选取垫座高度为30、32、35、38、40、42、45、47 m，垫座厚度为12.5、15.5、18.5、21.5、24.5 m，垫座底面圆心角为20°、40°、52°、68°、84°等情况下进行综合分析。计算采用三维几何模型、六面体单元网格，利用有限元分析软件Abaqus分析了坝体应力，模型尺寸约为250 m× 438 m× 156 m，模型底部及四周边界上的节点仅受法向约束，并采用Fortran编程计算坝体及垫座的等效应力。网格模型如图2所示。

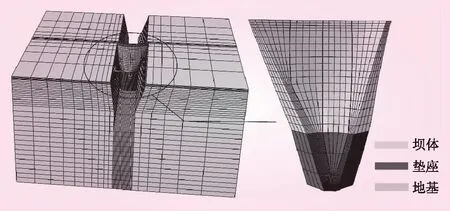
图2 模型有限元网格

考虑的基础荷载包括地应力、垫座自重、坝体自重、水荷载和温度荷载。由于坝体的常效运行状态为正常蓄水位，因此本次计算水位选用正常蓄水位；同时据研究表明，温降情况下坝体拉应力较大，故本次计算只对温降情况进行分析。坝体及地基各材料的物理力学参数标准值见表1，其中在计算过程中，模拟了坝体施工和封拱的过程。

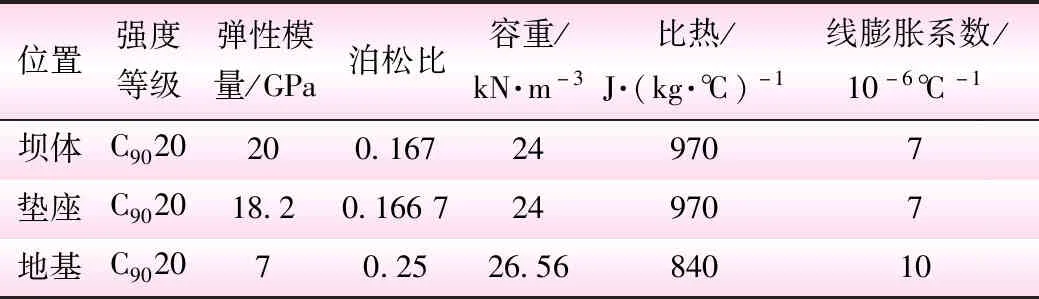
表1 坝体、垫座及地基各材料的物理力学参数

2.2 计算结果分析

通过对不同垫座体形尺寸计算得到的坝体等效应力结果分析可知，坝体最大等效拉、压应力在不同垫座高度的变化规律基本保持一致，且与垫座高度呈负相关。为了更直观地体现垫座体积及坝体最大等效拉、压应力与模型中3个参数的关系，绘制了垫座高度为30、35 m时的垫座体积变化规律如图3所示，以及坝体最大等效拉、压应力变化规律如图4所示。

图3 垫座高度为30、35 m时垫座体积的变化规律

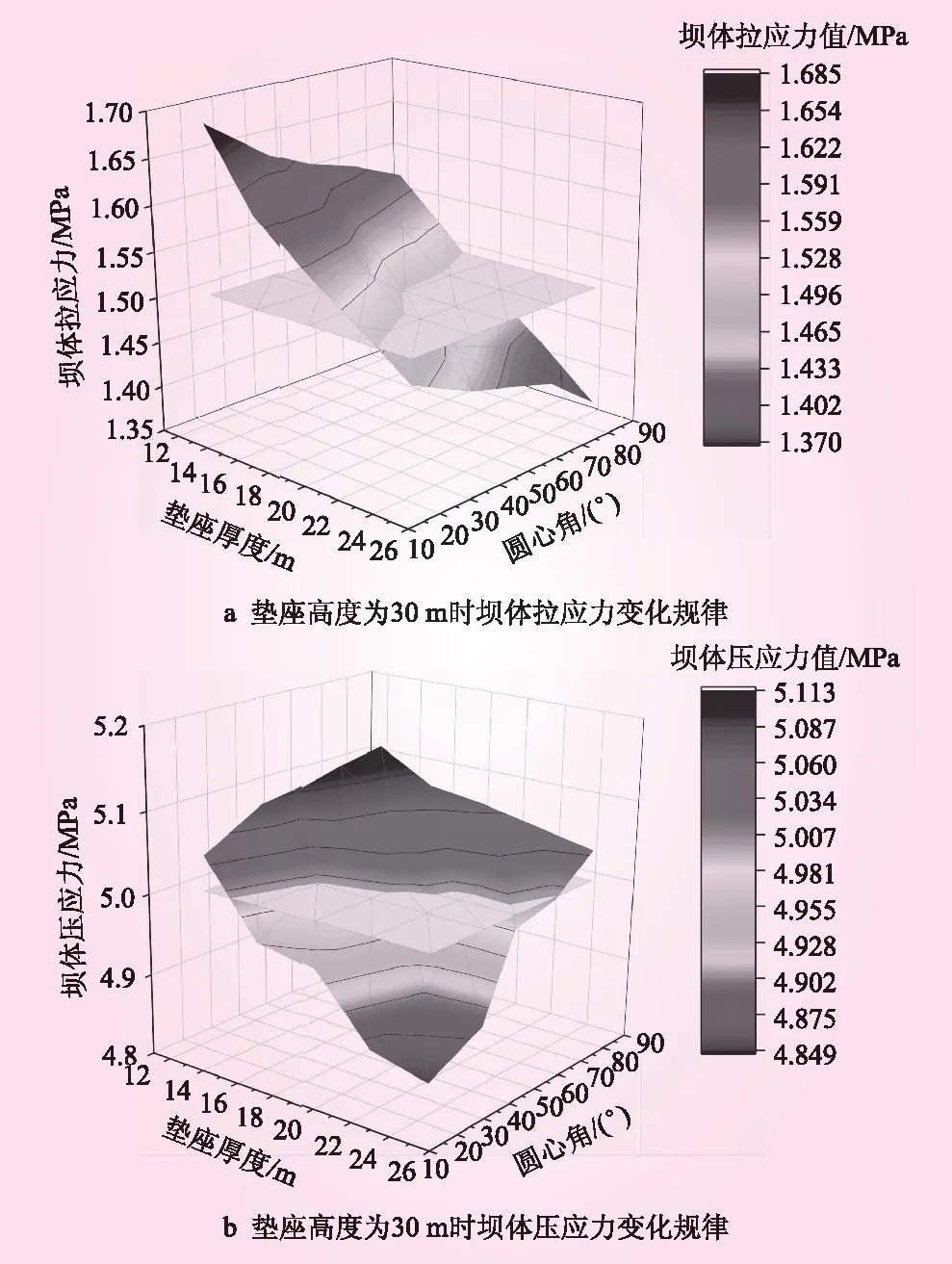
图4 垫座高度为30 m时坝体应力变化规律

从图3可知，垫座体积随圆心角及厚度的增大而减小，且沿Y轴向的倾斜程度要略大于X轴向与Z轴向。对于本文中的圆弧形拱坝，根据其几何特征，增加相同程度的量值，其厚度对垫座体积的影响要略大于垫座底面圆心角度数与垫座高度对垫座体积的影响。

从图4a可知，坝体最大等效拉应力随垫座厚度及圆心角的增大而减小，且垫座厚度较小时，其拉应力值已超过规定的允许值；从图4b可知，坝体最大等效压应力随垫座厚度的增大而减小，而随圆心角的增大而增大，且垫座较小，圆心角较大时，其压应力值已超过规定的允许值；对比分析图图4a、b，当垫座厚度较大，圆心角偏小时，坝体最大等效拉、压应力均小于允许值。这是由于垫座增厚以后，地基的整体性变强，地基承担的沉降较均匀，而坝体在自重作用下沉降量变小所导致的。

2.3 优化结果

根据每一高程垫座体积、坝体最大等效拉、压应力与垫座3个体形参数的关系，可求得在满足约束条件下，使得体积最小3个体形参数的取值，即为该高程的最优点。同理可求得每一高程的最优点，再比较最优点相对应的体积大小，则体积最小值所对应的体形参数即为所求垫座体形的优化尺寸。由图3、4可知，当垫座厚度在19～22 m，垫座底面圆心角在40°～52°时，坝体最大等效拉、压应力均小于其规范允许值，再根据相应的体积变化规律，确定垫座高度为30 m时垫座的最优体形参数为：d=21.5 m，n=50°，此时v=19 073.77 m3。由此可求得每一垫座高度下的垫座体形的最优点，综合考虑垫座3个体形参数以及垫座体积，绘制出在不同高度下垫座体形的最优取值如图5所示。

图5 不同垫座高度垫座优化取值

不同垫座高度垫座体积变化见图6。从图6可知，当垫座高度为35时，垫座体积取得最小值，为186 269.70 m3，此时d=19 m，n=45°，因此该工程的最优垫座尺寸为：h=35 m，d=19 m，n=45°。

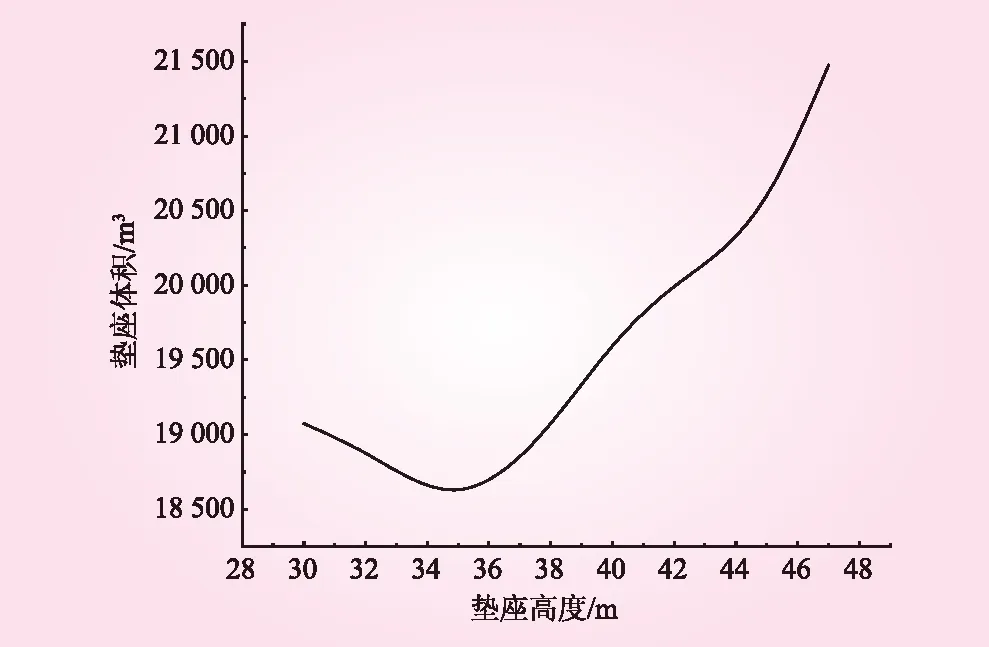
图6 不同垫座高度垫座体积变化规律

3 结 论

针对工程中常见的垫座问题，本文提出三参数优化模型，并采用有限元等效应力法对工程实例进行了分析，研究了不同的垫座设计方案，对比分析了坝体在不同垫座高度、厚度、圆心角度数下的应力情况，综合考虑了坝体稳定性，并结合垫座的经济性对垫座形式进行了优化，得到以下结论：

(1)本文三参数优化模型采用垫座高度、厚度以及底面圆心角度数3个参数，其可综合考虑垫座结构尺寸对坝体的影响及其对工程的经济适用性，简单可行。

(2)对于扇形垫座，在坝体应力合理的范围内，适当地减小垫座高度及厚度，有助于减小垫座体积，节省相应的工程成本。

(3)三参数目标优化模型丰富了垫座优化问题的计算方法，采用三参数模型对垫座进行优化设计可以为类似工程提供参考。