降雨量突变对水库汛期分期及调度影响研究

贾振兴

(山西省水资源研究所，山西 太原 030001)

0 引 言

汛期分期是根据暴雨洪水在不同时期所表现出的差距而进行划分的[1]。科学的汛期分期是水库调度的前提[2]。近百年来全球气候变暖，导致降雨量时空分布发生改变[3-4]。在水库调度运行中，降雨量是决定汛期时间节点的关键因素，降雨量时空分布的改变会引起汛期分期的变化，而现行的汛期分期根据多年降雨资料获得的，缺乏了对降雨量变化条件的考虑[5]。因此，本文采用量变质变判别模以张家庄水库降雨量突变点为分界点，对突变点前后张家庄水库进行汛期分期，并建立汛期分期评价指标，对分期结果进行评价，再分别以传统汛期分期结果与气候突变年后汛期分期结果为标准，对张家庄水库进行调度研究，明确降雨量突变对汛期分期时间节点变化与水库调度的影响。

1 理论基础

1.1 量变质变判别模式的汛期分期

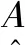
1.1.1步骤1

构建n个指标特征值矩阵

(1)

式中，xim为时序m指标i特征值。

1.1.2步骤2

确定时序研究对象ut指标i的特征值xim落入汛前期与主汛期或主汛期与后汛期相对隶属度为1的标准值区间矩阵[Ni1，Ni2]，已知矩阵X，可得标准区间矩阵。其中，i=1，2，3…n;h=1，2则

Ni1=(minxim，maxxim)，Ni2=(maxxim，minxim)

(2)

式中，maxxim、minxim分别为时序集xim的最大、最小特征值。

1.1.3步骤3

计算xim落入[Ni1，Ni2]区间的相对隶属度

(3)

1.1.4步骤4

根据主成分分析法确定各指标的权重wi。

1.1.5步骤5

计算ut综合相对隶属度

(4)

式中，α为优化准则参数；P为距离参数。α=1为最小一乘方优化准则，α=2为最小二乘方优化；考虑到α=2对距离具有放大或缩小效应，因此在汛期分期的应用中，选取α=1。

若采用优化准则参数α=1，距离参数为海明距离，即P=1，则式(4)变为线性公式

(5)

若汛期分期为非线性系统，可采用欧氏距离，即P=2，式(13)变为

(6)

1.1.6步骤6

1.1.7步骤7

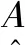
(7)

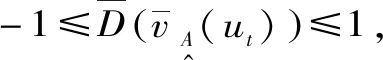
1.1.8步骤8

应用质变与量变判别模式分析汛期演变规律。

1.2 扫描式滑动t

传统的滑动t检验法对突变点的检验结果依赖于子序列的选取，为克服滑动t检验对子序列选取的依赖性，扫描式滑动t检验对所有子序列进行趋势检验，得到t的中心值，中心值的极值则为突变发生所对应的时间节点。t统计量计算步骤如下

(8)

(9)

(10)

通过改变n值实现对多尺度检验。n=2，3，…，N；N是时间尺度最大取值。当时间为i时，中心值t(n，i)取到极值，对应的时间尺度为n，即为突变时间点。

1.3 Cumulative Sum of rank Difference趋势检验法

Cumulative Sum of rank Difference(CSD)趋势检验利用了图形诊断和统计分析，由Charles Onyutha于2017年开发，且已经被很好地应用于评估水文气象学的变化[6-8]。因此，本文采用CSD检测法对汾河流域降雨量变化趋势检验。具体步骤如下：

(1)X表示已知的数据系列，则时间序列Y可以通过对X的复制得到。则可以得到数据点的超越和非超越计数的重标时间序列c。即

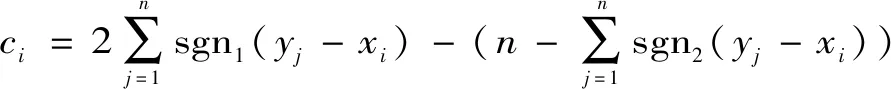
(11)

(2)计算趋势统计TCSD。即

(12)

TCSD的正/负值表示上升/下降的线性趋势。TCSD的分布与Onyutha所给出的零和方差(V1)的均值近似接近正态分布

(13)

式中，b是数据中联系的度量

(14)

(15)

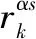
(16)

(17)

用于检测rk显著性的(100-αs)%置信区间CL可以用下式计算。即

(18)

累积和序列(Csum)可由方程(11)获得第i处的累计和值

(19)

从图形上说，Csum，i可以依据i或者观察时间来绘制来识别系列中的变化。

2 实例分析

2.1 降雨量突变年检验

张家庄水库位于山西省孝义市新城南。对张家庄水库1969年～2015年降水量进行了扫描式滑动t检验，结果如图1所示。等高线图对应的t最大值为4.496，相应年是1995年。这意味着张家庄水库1969年～2015年间降雨量在1995年发生了突变。

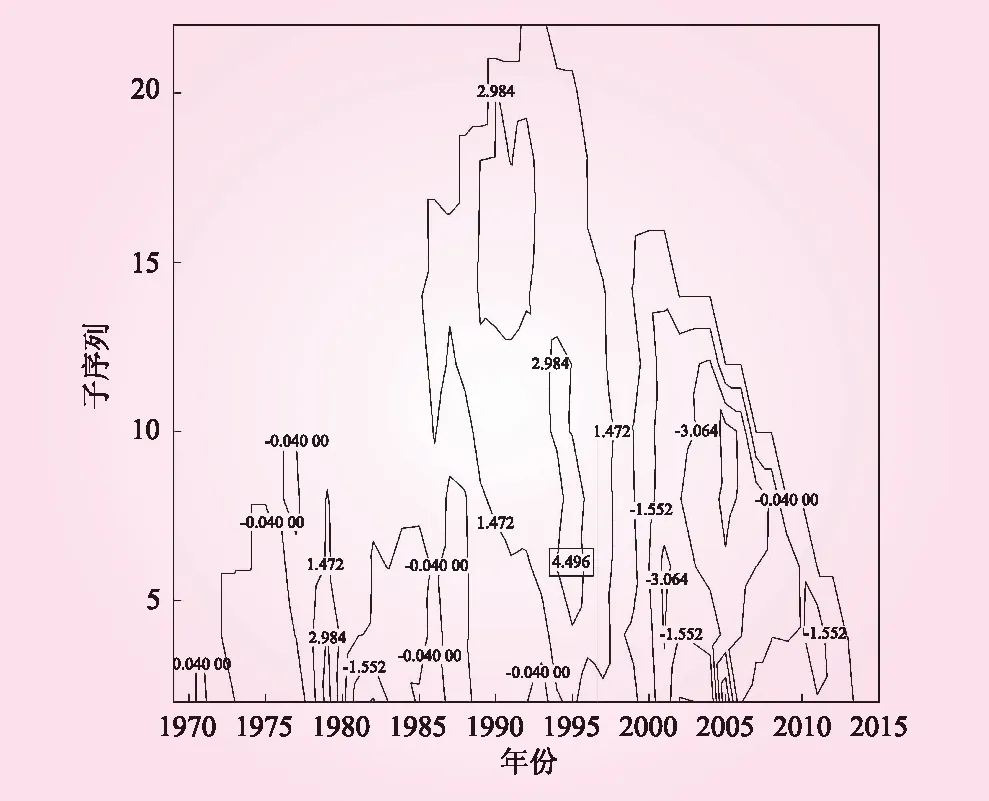
图1 1969年～2015年降雨量滑动式扫描t检验结果

CSD检验结果见图2。以Csum=0线为参考，累积和以参考值的偏差表征了该系列中的时间变化。当系列值子周期的时间序列以随机变化为特征时，在另一部分则具有线性趋势；而在具有线性趋势的部分上将形成曲线的趋势[7]。因此，从图2系列趋势分析可以得到，在0～25序列之间，以随机变化为特征的序列，对应图2b中的线性趋势；但在26～50序列之间，以线性递减趋势为特征，该趋势对应图2b中26～50序列号之间的曲线的趋势。对于一个序列在第一部分没有趋势，但在第二部分有线性增加或减少，变化点是曲线开始的地方；所以可以从图2b中得到变化点，它是对应于最大异常值即第26个时间序列。由此可得出，1969年～2015年降水量的变化规律，1969年～1994年降水量无明显变化趋势，1995年～2015年有减少趋势。降水突变点为1995年，与扫描式滑动t检验结果一致。因此，本研究认为1995年是该地区降雨的突变点。

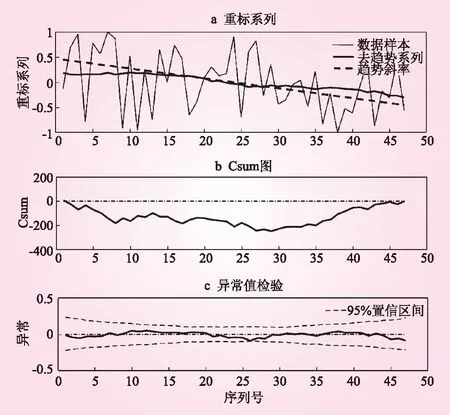
图2 1969年～2015年降雨量CSD检验结果

2.2 判别模式汛期分期

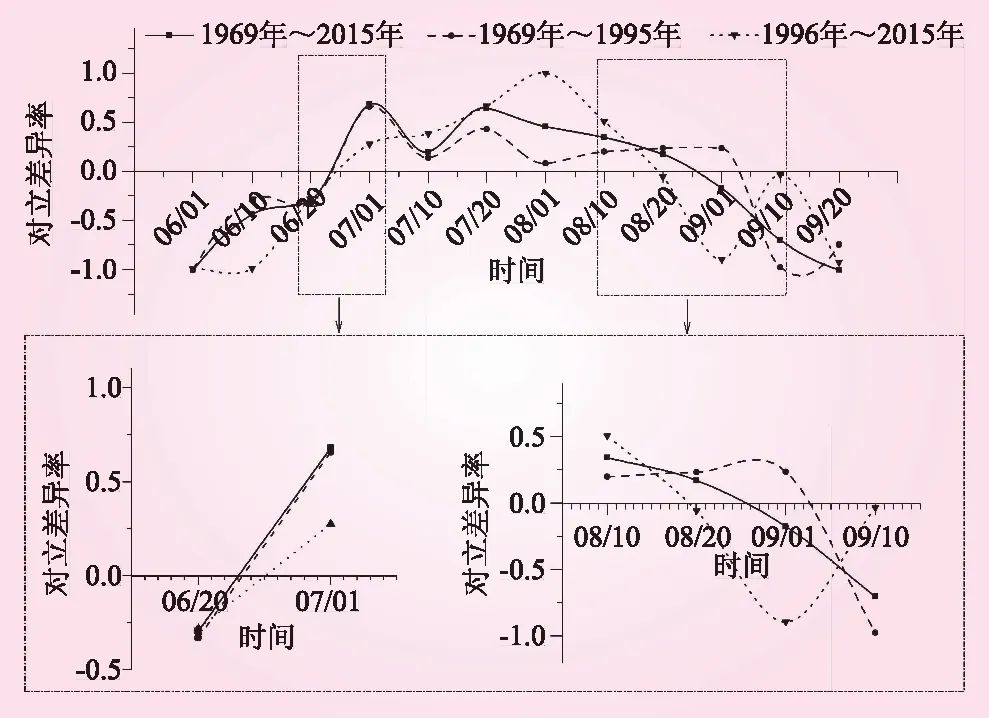
图3 1969年～2015年、1969年～1995年和1996年～2015年对立差异度

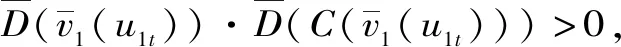
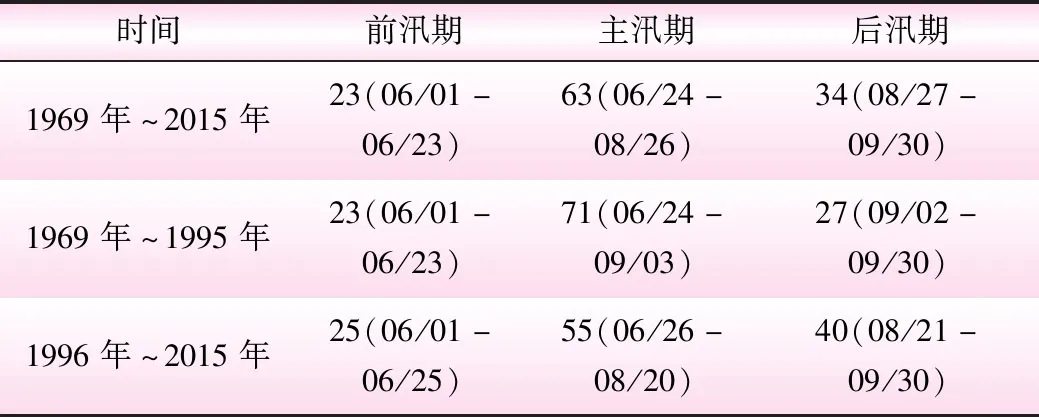
表1 汛期分期结果 d

2.3 分期结果评价及对比

这里选取张家庄水库1969年～2015年汛期(06/01-09/30)逐日降雨量作为汛期水库的特征指标量，取个时段均方差评价指标S作为评价因子[6]，在3组不同的权重组合下分期结果评判指标S结果见表2。

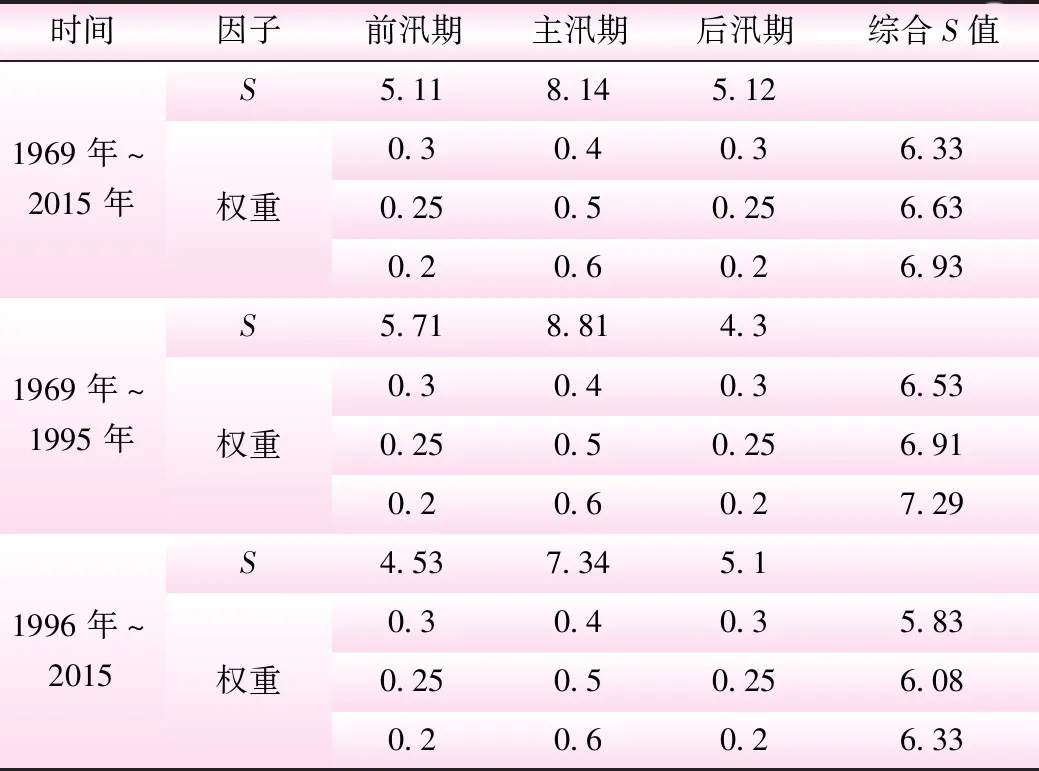
表2 汛期分期结果评价

由表2可知，量变质变判别模式各分期的均方差均值及3组不同权重因子下所得到的突变年后的S值均小于由整时段所得，表明对气候突变年后的汛期分期效果相对于整体更接近实际，在汛期分期中考虑降雨量时空分布的改变是十分必要的。

3 不同汛期分期下的水库调度

张家庄现行主汛期汛限水位为762.00 m，后汛期为正常蓄水位764.00 m，汛期水库允许最高洪水位为设计标准洪水位766.36 m。本文以主汛期的汛限水位为起调水位，计算了整个时段与突变年后不同标准的降雨量及设计洪水过程线，得到突变年后与整个时段得到的水库调洪最高水位都小于防洪高水位766.36 m。假设上游来水可使水库在8月20日～26日蓄至正常蓄水位764.00 m，则以气候突变年后得到的主汛期为标准，8月20日水库水位超过762.00 m不需要弃水，可比以整个时段计算得到的主汛期为标准的水库调度方式多蓄水274万m3，可有效改善水库下游水资源利用条件、缓解水库供水压力[9]。

4 结 论

本文研究表明，考虑降雨量突变，以1969年～2015年时段计算得到的张家庄水库主汛期比1996年～2015年时段延长8 d，但比1969年～1995年时段计算的短9 d。降雨变化条件下的汛期分期结果在实际运用中会对水库调度运行等产生巨大效益。对张家庄水库而言，若上游来水可使水库在8月20日～26日蓄至正常蓄水位764.00 m，则考虑降雨量时空分布变化的水库调度方式可比传统的水库调度方式多蓄水274万m3。