考虑体形影响的特高拱坝施工期坝基变形统计模型研究

赵 程，李 倩，郑晓红

(1.国家能源局大坝安全监察中心，浙江 杭州 311122;2.中国电建集团华东勘测设计研究院有限公司，浙江 杭州 311122)

0 引 言

目前，高坝破坏机理和风险分析等涉及高坝安全的理论研究尚不够完善，安全监测是施工期高拱坝监控预警以及反馈分析的主要手段[1]。其中，大坝变形是对大坝安全状况的最直观和有效的反映。大坝变形监测统计模型由于其建模相对简单，理论相对成熟，已成为施工期大坝变形分析、预测的主要方法之一。

传统的施工期坝基变形监测统计模型主要考虑大坝浇筑高度、水压、温度、降雨以及时效变形的影响[2-3]，其中，施工期坝体浇筑高度变化是坝基变形的主要影响因素，传统的监测统计模型中浇筑高度分量只考虑坝体浇筑高程变化的影响，然而拱坝体形沿高程是不断变化的，双曲拱坝在浇筑过程中坝体还会出现倒悬状态，不同高程相同高度的浇筑块对基础的影响效应是不同的，所以单纯考虑坝体浇筑高度的影响是不合适的，因此本文引入竖向压重分量和弯矩分量来代替坝体浇筑高度分量，建立考虑体形影响的特高拱坝施工期坝基变形统计模型。

1 施工期坝基变形监测统计模型

1.1 传统施工期坝基变形监测统计模型

已有的坝工知识和监测数学模型经验表明，拱坝施工期和蓄水期沉降的变化主要受坝体浇筑高度h、水压H、坝体温度T和时效等因素变化的影响，变形统计模型一般表达式为[2-4]

(1)

(2)

式中，a0为回归常数；ai、bi、ci、di为回归系数，均由回归分析确定；n1、n2、n3、n4分别为浇筑高度因子、水压因子、温度因子和时效因子个数；h(t)为t时刻的浇筑高度；H(t)为t时刻作用在大坝上的水压；Ti(t)为t时刻温度测点i的温度测值；Ii(t)为时效因子。

1.2 传统施工期坝基变形监测统计模型的局限性

拱坝坝基变形监测施工期统计模型中，浇筑高度分量占主导因素，传统的施工期坝基变形监测统计模型中浇筑高度分量仅考虑浇筑块上升高度的影响。拱坝体形沿高程是不断变化的，不同高程同样高度的浇筑块体积是不一样的，基础上相应增加的应力也是不同的，浇筑块上升高度的影响应该等效换算成竖直向压重的作用；同时由于目前筑坝技术的发展，新建的特高拱坝体形逐渐多样化[5-6]，水平向及竖向大多均有一定程度的弯曲，这就导致了在浇筑过程中坝体会出现倒悬状态，倒悬状态下由于弯矩的影响，坝体作用于基础不同部位的应力明显不同[7-8]，这对基础变形会存在一定的影响。

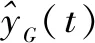
2 考虑体形影响的特高拱坝施工期坝基变形统计模型

2.1 竖向压重分量构建

拱坝单坝段浇筑示意见图1，一般拱坝浇筑层厚度约3 m，浇筑块厚度相对于拱坝总高度较小，每个浇筑块可当做长方体考虑，拱坝新浇筑块重力可表示为

ΔGi=γ×Li×Δhi×B

(3)

式中，ΔGi为新浇筑块重力；γ为混凝土容重；Li为新浇筑块上下游向长度；Δhi为新浇筑块高度；B为坝段宽度。

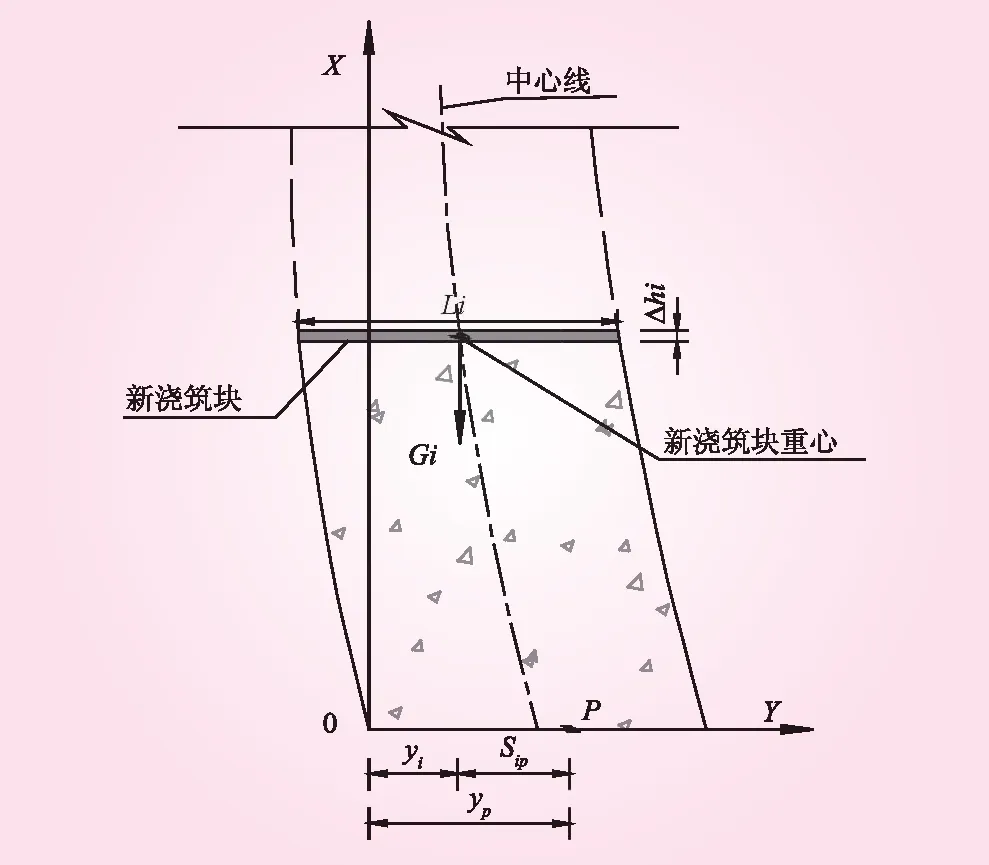
图1 拱坝单坝段浇筑示意

作用于基础部位的重力Gi为已浇筑混凝土累积重力，为各个浇筑块重力之和，可表示为

(4)

式中，Gi为浇筑块总重力；n为浇筑块个数。

yh(t)=f{h(t)，h2(t)，h3(t)，h4(t)}

(5)

竖向压重分量是将浇筑块上升高度的影响等效换算成竖直向压重的作用，则任一浇筑高度情况下混凝土重力对变形的贡献量yG(t)为

yG(t)=f{h(t)，h2(t)，h3(t)，h4(t)}×L×B×γ=f{G(t)，G2(t)，G3(t)，G4(t) }

(6)

(7)

式中，a0、aj分别为回归常数和为回归系数，a0、aj均由回归分析确定；m为压重因子个数。

2.2 弯矩分量构建

拱坝弯矩分量主要考虑施工期间倒悬状态的影响，倒悬对基础变形的影响主要体现在坝体作用于基础不同位置的弯矩是不一样的，进而导致基础变形的差异性。拱坝单坝段基础不同位置弯矩作用示意见图1，则新浇筑块作用于基础上任一点p的力臂长度为

Sip=yp-yi

(8)

式中，Sip为新浇筑块作用于基础上p点力臂长度；yp为p点Y向坐标；yi为新浇筑块重心的Y向坐标。

新浇筑块作用于点p的弯矩ΔMip为

ΔMip=Gi×Sip

(9)

作用于基础点p部位的弯矩Mip为已浇筑混凝土的累积弯矩，可表示为

(10)

式中，Mip为浇筑块作用于p点的总弯矩；n为浇筑块个数。

弯矩分量与竖向压重分量具有深刻内在联系，前面竖向压重分量与浇筑块重力的1～4次方有关，则任一浇筑高度情况下混凝土弯矩对变形的贡献量yM(t)为

yM(t)=f{G(t)，G2(t)，G3(t)，G4(t)}×S=

f{M(t)，M2(t)，M3(t)，M4(t)}

(11)

(12)

式中，b0、bj为回归常数分别为回归常数和回归系数，b0、bj均由回归分析确定；w为弯矩因子个数。

2.3 考虑体形影响的坝基变形统计模型构建

根据以上分析，拱坝施工期基础变形主要受浇筑混凝土竖向压重G、弯矩M、水位H、温度T以及时效等因素变化的影响，其中温度对拱坝施工期基础变形相对于其他几个因素的影响可忽略不计，则考虑体形影响的坝基变形统计模型一般表达式为

(13)

式中，a0为回归常数；aj、bj、cj、dj为回归系数，均由回归分析确定；n1、n2、n3、n4分别为压重因子、弯矩因子、水位因子以及时效因子个数。

3 工程实例

3.1 工程简介

白鹤滩水电站位于金沙江下游四川省境内，是一座以发电为主的综合水利枢纽。枢纽工程主要由混凝土双曲拱坝、二道坝及水垫塘、泄洪洞、引水发电系统等建筑物组成。其中，混凝土双曲拱坝坝顶高程834.00 m，最大坝高289.0 m，其中15～21号坝段为表孔和深孔坝段，16～20号、22号坝段为底孔坝段，其他坝段为挡水坝段。

为监测河床坝段基础沉降的变化情况，在河床18号坝段的坝踵、坝中以及坝趾附近分别布置一套多点变位计(MZJJ18-1～MZJJ18-3)，选取多点变位计2017年4月(始测)至2019年4月初共119个测次的孔口变形值作为样本，按本文提出的建模方法构建考虑体型影响的坝基变形统计模型。白鹤滩水电站大坝及18号坝段多点变位计布置见图2。

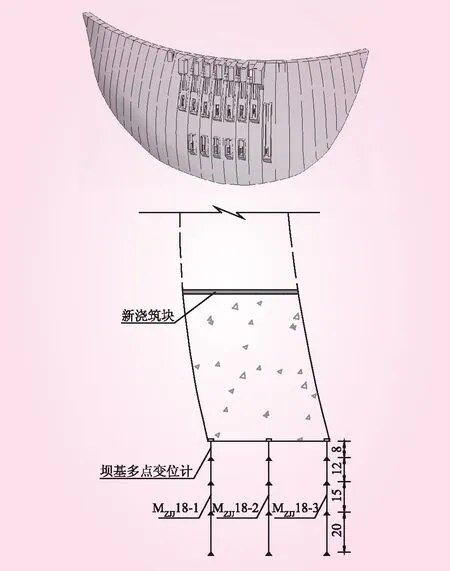
图2 白鹤滩水电站大坝及18号坝段多点变位计布置示意

3.2 模型的建立

3.2.1竖向压重分量的构建

构建竖向压重分量之前，首先计算浇筑块重力Gi，计算方法见式(3)和式(4)，其中混凝土容重γ和坝段宽度B是常数，单个浇筑块高度Δhi根据施工记录得到，浇筑块上下游向长度Li需要计算。Li计算简图可参见图1，坝体高度X方向每间隔10 m量取坝体上下游向仓面长度L，采用多项式拟合曲线见图3，可得18号坝段浇筑块上下游向长度L随坝体高度变化的方程为L=-8×10-7h3-0.000 3h2-0.018 9h+63.503。

图3 上下游向长度随坝体高度变化曲线

18号坝段基础竖向压重分量构成可表示为

(14)

式中，a0、aj为回归系数、均，由回归分析确定；γ和B均是常数；Li为浇筑块长度根据式；Δhi(t)为浇筑高度根据施工记录得到；n为浇筑块个数，m为压重因子个数。

3.2.2弯矩分量的构建

新浇筑块作用于基础上p点力臂长度Sip需要计算求得。Sip的计算简图见图1，当每个新浇筑块当做长方体考虑时，新浇筑块重心位于横断面中心线上，坝体高度X方向每间隔10 m量取断面中心线坐标Y，采用多项式拟合曲线见图4，可得18号坝段断面中心线(浇筑块重心)随坝体高度变化的方程为y=0.001x2-0.2722x+31.351。

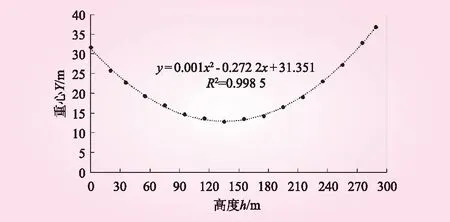
图4 断面中心线(浇筑块重心)随坝体高度变化曲线

进一步根据式(8)可求得力臂长度Sip，则18号坝段弯矩分量构成可表示为

(15)

式中，b0、bj均为回归系数，、均由回归分析确定；Gip为浇筑块重力根据式(n为浇筑块个数，w为体形因子个数。

3.2.3模型的构建

根据式(13)，考虑体形影响的坝基变形统计模型分量一般由竖向压重分量、弯矩分量、水位分量以及时效分量组成，目前白鹤滩水电站大坝未下闸挡水，计算时暂不考虑水位分量，时效分量按照传统统计模型预置，则建立的18号坝段考虑体型影响的坝基变形统计模型表达式为

3.3 建模结果分析

统计模型常用复相关系数R和剩余标准差S来评判其精度。复相关系数是判断回归有效性的重要指标，复相关系数越大，回归方程的质量越高；剩余标准差S反映了所有随机因素及方程外的有关因子对监测效应量的平均变差的大小，是回归方程精度的重要标志，剩余标准差越小，说明回归方程的精度越高[2-4]。

考虑体形影响的坝基变形统计模型建模精度和传统统计模型精度对比见表1，本文模型计算得到各测点孔口位移拟合值变化过程线见图5，由图5可知，相对于传统施工期变形监测统计模型，本文考虑体形影响的坝基变形统计模型复相关系数R较高，剩余标准差S较低，模型质量和精度更高。从分量入选结果来看，目前18号坝段基础的时效变形不明显，变形主要受当天和前一天浇筑块重力和弯矩作用的影响。

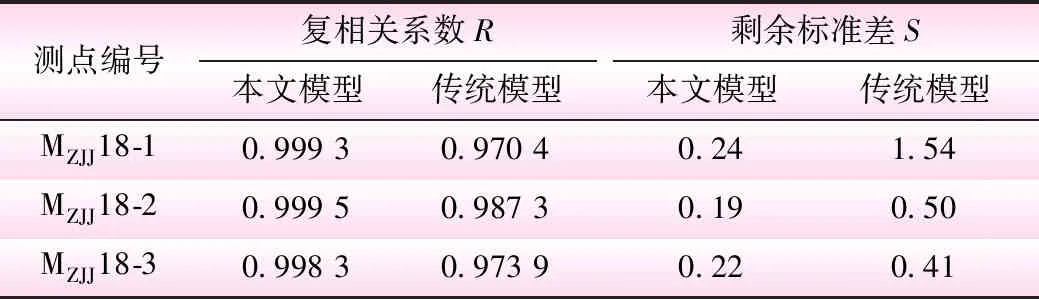
表1 模型精度对比

此外，为验证本文所建立的考虑体形影响的坝基变形统计模型的预测效果，本文还建立了传统的监测统计模型，采用2种模型同时对MZJJ18-2测点2019年4月～5月共计8个测次的坝基变形进行检验性预测，结果见表2。由表2可知，本文模型预测精度较高，各预测值相对误差均在±2%以内，进一步说明本文所提出的考虑体型影响的坝基变形统计模型合理有效。

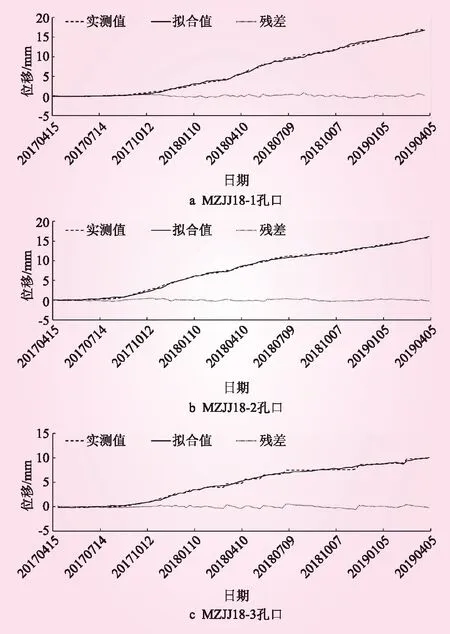
图5 位移拟合值变化过程线

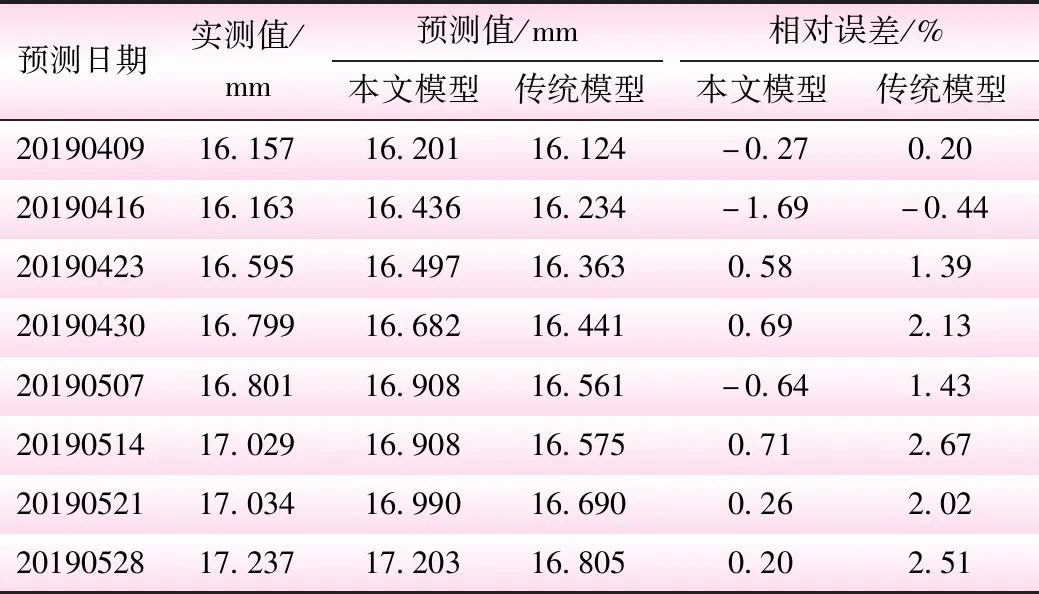
表2 本文模型与传统统计模型预测结果

5 结 语

本文引入竖向压重分量和弯矩分量代替传统的坝体浇筑高度分量，建立考虑体形影响的特高拱坝施工期基础变形统计模型。实例分析表明，截止2019年4月初，白鹤滩18号坝段浇筑高度139.80 m，目前该坝段基础的时效变形不明显，变形主要受当天和前一天浇筑块重力和弯矩作用的影响；与传统统计模型相比，本文所提出的模型质量和精度更高，预报效果更好。但是，本文所提出考虑体形影响的监测统计模型是通过发掘大坝变形在时间序列上与施工过程、水位等内在的相关关系和演变规律，在建模过程中，未直接考虑地质因素、岩体弹塑性变化等对监测效应量的影响，这些影响整体上归纳到了时效因子当中，这对预测精度会存在一定的影响。