基于点估计理论滑坡稳定性及可靠度分析
易庆林,周 瑞,许 倩,陈 源,曾怀恩
(1.三峡大学三峡库区地质灾害教育部重点实验室,湖北 宜昌 443002;2.三峡地区地质灾害与生态环境湖北省协同创新中心,湖北 宜昌 443002;3.三峡大学湖北长江三峡滑坡国家野外科学观测研究站,湖北 宜昌 443002)
0 引 言
三峡工程自建成蓄水正常运行以来,库区长江两岸以及相关支流两岸附近的边坡变形和失稳现象愈加明显,库水位的升降使山体往复充水失水,再叠加雨水的冲刷和人类工程活动,造成了众多边坡失稳事件,也埋下无数安全隐患。因此,已有很多学者基于三峡库区蓄水的影响,进行了库水位升降对滑坡稳定性的研究,并获得了丰硕的研究成果。失稳滑坡中存在着诸多不确定因素,其孕育机理也有诸多不确定性,不确定分析更能合理地评价滑坡的稳定性[1]。易庆林等[2]通过分析三门洞滑坡体变形速率与降雨、库水位升降及速率得出,该滑坡为退水滞后型滑坡,且库水位升降和大气降雨为其主要影响因素。薛聪聪等[3]通过对三门洞滑坡渗流特征及稳定性分析得知,库水位上升为该滑坡稳定的有利因素,即一定程度能提高其稳定性,且库水位上升的有利因素优于大气降雨的不利因素。沈秋池等[4]以台风降雨和持续性强降雨2种雨型,对福建地区残积土边坡进行稳定可靠度分析,不同雨型在土体中渗透性不同,随持续时间对滑坡的稳定可靠度也随之变化。张亚国等[5]利用点估计法,对黄土边坡的4个工点考虑粘聚力c、内摩擦角φ对边坡可靠性进行分析。李杰[6]采用点估计法,考虑c、φ值对既有铁路边坡可靠性进行分析。以上分析证明了点估计法的分析结果更具有实用性和更符合工程实际需要。
本文同样利用点估计法,但分析对象为涉水水库型滑坡,考虑库水位下降和降雨为随机变量,对滑坡可靠度进行分析,为涉水型滑坡的其他影响因素变量的选取研究建立基础,为滑坡的预测分析提供理论依据。
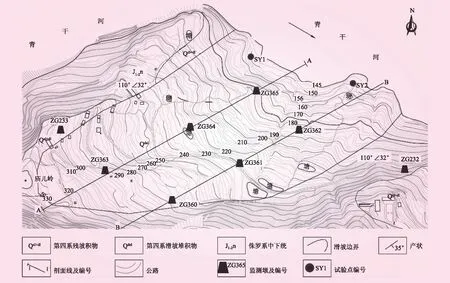
图1 滑坡工程地质平面
1 滑坡工程地质概况
三门洞滑坡地处秭归县沙镇溪镇梅坪村一组,位于长江某一级支流青干河右岸,距离集镇直线距离约2.5 km,距离入江河口直线距离约5.5 km,距离三峡工程坝址直线距离约43 km。根据气象资料,滑坡所在地气候温和,雨量充沛,年最大降雨量1 430.6 mm,日最大降雨量358 mm,降雨多分布在5月~9月,且多为暴雨,年降雨120~140 d。滑坡内地下水主要是基岩裂隙水和松散孔隙水,主要由大气降雨和库水上升补给,少量为农业灌溉。
滑坡工程地质平面见图1。从图1可以看出,滑坡平面形态呈舌状,整体呈圈椅状。岩层倾向与坡面角度相近,为顺向坡,西南角较高,东北角较低,由西南向东北直抵青干河。滑坡左右边界以陡坎和基岩山脊为界,后缘高程350 m,前缘高程位于水下,为140 m,平均坡度15°,长约830 m,均宽300 m,滑体面积约2 600 m2,平均厚度约22 m,滑坡体积约5.7×104m3,主滑方向约为60°。
根据现场踏勘资料,该滑坡体物质主要由第四系残坡积碎石土组成,主要有石英砂岩、泥岩、粘土、砂土等。滑面为上覆土层与基岩的接触面,滑床由浅灰色或紫红色的泥岩和泥质砂岩组成的斜顺向坡。
2 滑坡可靠度分析模型的建立
传统的确定性分析评价滑坡的稳定性通常只考虑安全系数,而实际上边坡稳定性受诸多方面影响,是一个非常复杂的问题。不确定性分析是建立在影响安全系数的每个因素的标准差和均值的定量分析,以及假设其安全系数服从某概率模型的基础上,计算所得滑坡失效的概率。不确定分析的优点就是能对每个影响因子自身所包含的不确定性予以考虑[1]。
2.1 基本原理
当前,比较多用的可靠度分析方法主要有蒙特卡洛法(Monte Carlo method)、一次二阶矩法(FOSM)、点估计法[5-8]。蒙特卡洛法需要取足够大的样本数目以及可靠的抽样随机性,这是其精度要求的重要保障;一次二阶矩法则需要多次迭代求解,在实际工程应用中有一定局限性;点估计法又叫做Rosenbleuth法,由Rosenbleuth在1975年提出的一种通过点估计的方式计算滑坡工程中的可靠度指标。
2.2 滑坡极限状态方程
该滑坡稳定性受库水位、气候水文、人类工程活动、岩土体物理力学参数、上覆荷载等诸多因素的影响,最主要的是因素是库水位和降雨,功能函数Z表示为
Z=F(X1,X2,…,Xn)-1
(1)
式中,F为滑坡稳定性系数;Xn随机参数。Z>0,滑坡处于稳定阶段;Z=0,滑坡处于临滑状态;Z<0,滑坡已经失稳滑动。极限状态方程可表示为
F(X1,X2,…,Xn)-1=0
(2)
2.3 点估计法原理
点估计法要求由随机变量计算的均值和标准差生成若干个点,再从这若干个点中估计功能函数的值,从而通过简单的计算获得其可靠度指标。本文主要考虑库水位下降速度和降雨这2个变量,则相应的取值为
(3)
式中,W+为库水位从175 m水位以速度v1下降;W-为从175 m水位以速度v2下降;R+为有降雨情况;R-为无降雨情况;μW、μR分别为W、R取值的均值;σW、σR分别为W、R取值的标准差。
通过以上组合变换,可得到4种不同的稳定性系数组合,即
(4)
式中,F++为库水位从175 m水位以速度v1下降和降雨时的稳定性组合;F+-为从175 m水位以速度v1下降和无降雨的稳定性组合;F-+为从175 m水位以速度v2下降和降雨时的稳定性组合;F--为从175 m水位以速度v2下降和无降雨时的稳定性组合。
考虑2种随机变量时有4种组合方式,有n种随机变量时有2n种组合方式。因为所计算的是样本标准差,所以标准差公式根号内除以(2n-1),将由下式计算稳定性系数的均值μF和标准差σF
(5)
(6)
用β表示可靠度指标,公式为
(7)
滑坡失稳破坏的可能性为失效概率,相应的失效概率pf为
Pf=p(Z<0)=P[F(W,R)<1]
(8)
或
Pf=1-Φ(β)
(9)
式中,Fi为组合内的稳定性系数;Φ(β)为标准正态分布函数,可通过查询标准正态函数分布表取值。
3 滑坡稳定性及可靠度分析
3.1 模型建立与参数设置
建立滑坡有限元模型,通过有限元分析软件GEO-studio中SEEP/W模块进行渗流分析,再代入SLOPE/W模块进行稳定性分析得出滑坡的稳定性系数。本模型选取变形最大、最靠近滑坡中轴线的A-A剖面为计算剖面,网格模型见图 2。共划分1 985个节点,1 899个单元。
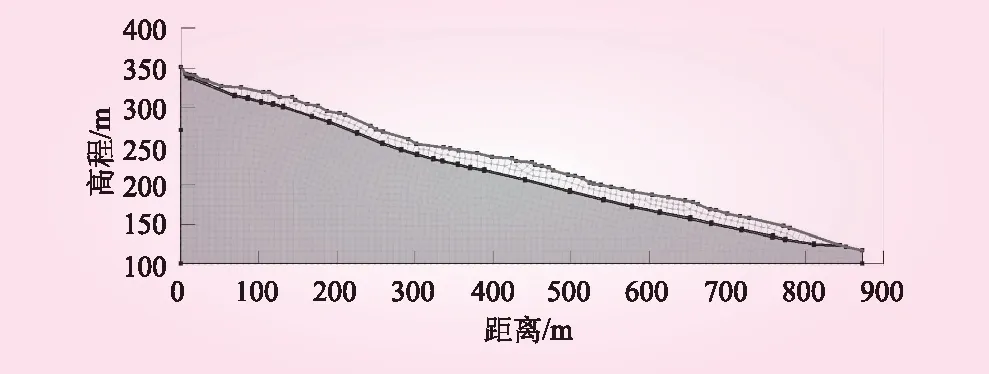
图2 A-A剖面网格模型
三门洞滑坡缺乏相关勘察资料,但与卧沙溪滑坡相距几百米,故该滑坡岩土物理力学参数根据卧沙溪滑坡相关勘察资料取值也是合理的[9]。岩土物理力学参数见表1。
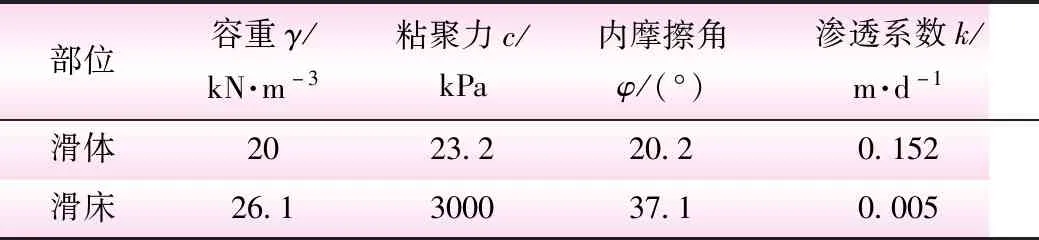
表1 岩土物理力学参数
3.2 工况设置
本文以中国长江三峡集团总公司所公布的实时水位,对2018年全年的水位变化情况进行统计分析,取下降幅度最大的5月份(水位变化见图 3)再次进行分析计算,由式(5)得出库水位下降速率的均值μW=0.369 m/day,由式(6)得出标准差σW=0.305。由式(3)计算可靠度指标,即
W+=μW+σW=0.674
W-=μW-σW=0.064
(10)
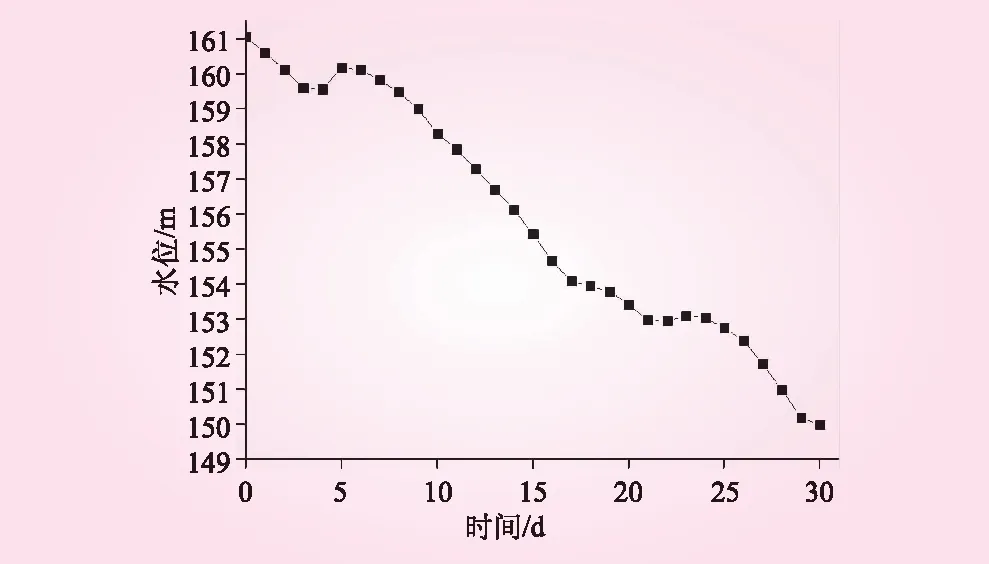
图3 2018年5月三峡库区水位变化
再根据2018年的降雨情况,取平均降雨量最大的5月份(日降雨量变化见图4)进行统计分析,得出库水位下降速率的均值μR=5.91 mm,标准差σR=13.40。计算可靠度指标如下
R+=μR+σR=19.31
R-=μR-σR=-7.49
(11)
式中,负值按照无降雨情况处理。
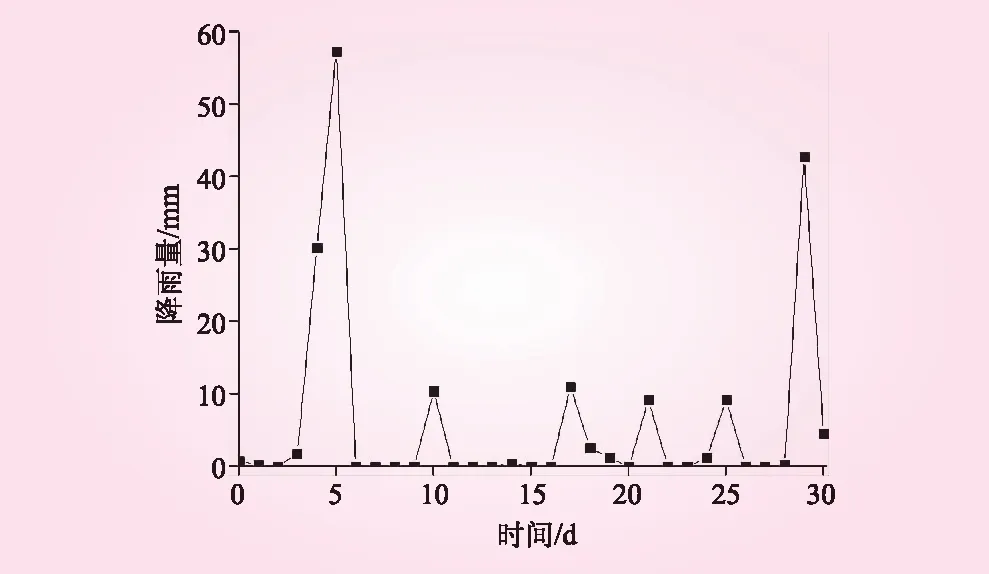
图4 2018年5月日降雨量变化
根据以上分析计算,模拟15d的库水下降和降雨情况,设定工况如下:工况1:降速0.674 m/day+降雨19.3 mm/day;工况2:降速0.674 m/day+无雨;工况3:降速0.064 m/day+降雨19.3 mm/day;工况4:降速0.064 m/day+无雨。
3.3 边界条件
初始地下水位线由野外勘测资料合理计算所得。模型边界条件:145~175 m水位范围内为变水头边界;边界函数为2018年库水位下降幅度最大的5月份库水位变化;库水位以上为潜在渗流边界;模型底部为不透水层。
3.4 稳定性分析
采用极限平衡法,模拟出4种工况的稳定性结果,见图5。从图5可以看出:
(1)在库水位相对较高降速和降雨情况下,滑坡稳定性呈现不均匀下降的趋势,且越往后下降趋势越明显,曲线呈上凸形。分析认为,三门洞滑坡体由粘土、碎块石土组成,渗透性差,降雨很容易形成坡面径流,随着从高处往低处流动,速度与动能增大,对坡面冲刷形成沟壑或小型塌陷,且从坡顶至坡脚的冲刷逐渐加重,使雨水从新造成的地表裂缝或已有裂缝入渗,并结合库水下降的滞后作用,存留在坡体内的地下水使得土体趋于饱和;随着降雨历时增加和库水的下降,越来越多滑体逐渐被软化,下滑力增大,阻滑力减小,稳定性也越来越差,也就造成曲线斜率越来越大。
(2)在库水位相对较高降速和无雨情况下,滑坡稳定性呈现均匀下降的趋势,但前期曲线斜率较工况1小,其曲线大致呈现线性曲线。分析认为,单纯的库位水下降和滑坡稳定性下降呈线性关系,使得曲线斜率均匀。
(3)在库水位相对较低降速和降雨情况下,滑坡稳定性呈现小范围上下波动的趋势。分析认为,存在轻微的浮托作用[10]使稳定性系数略有波动。所谓浮托作用是库水位在缓降的过程中,因土体渗透性较差,不能很快渗出坡体,此时,坡体内有地下渗流,坡脚处有库水阻滑压脚,使坡体内产生微小的方向向上的静水压力作用,即扬压力,所以稳定性会轻微增大。浮托作用达到一定程度,随着地下水渗出后,稳定性会再减小,这是稳定性波动的主要原因,但波动幅度在0.001精度左右,可认为稳定性基本不变。
(4)在库水位相对较低降速和无雨情况下,滑坡稳定性在前期基本不变,而在后期略微有所下降。分析认为,低速库水位下降对滑坡稳定性影响较小,10 d仅下降0.001,基本可认为不变。
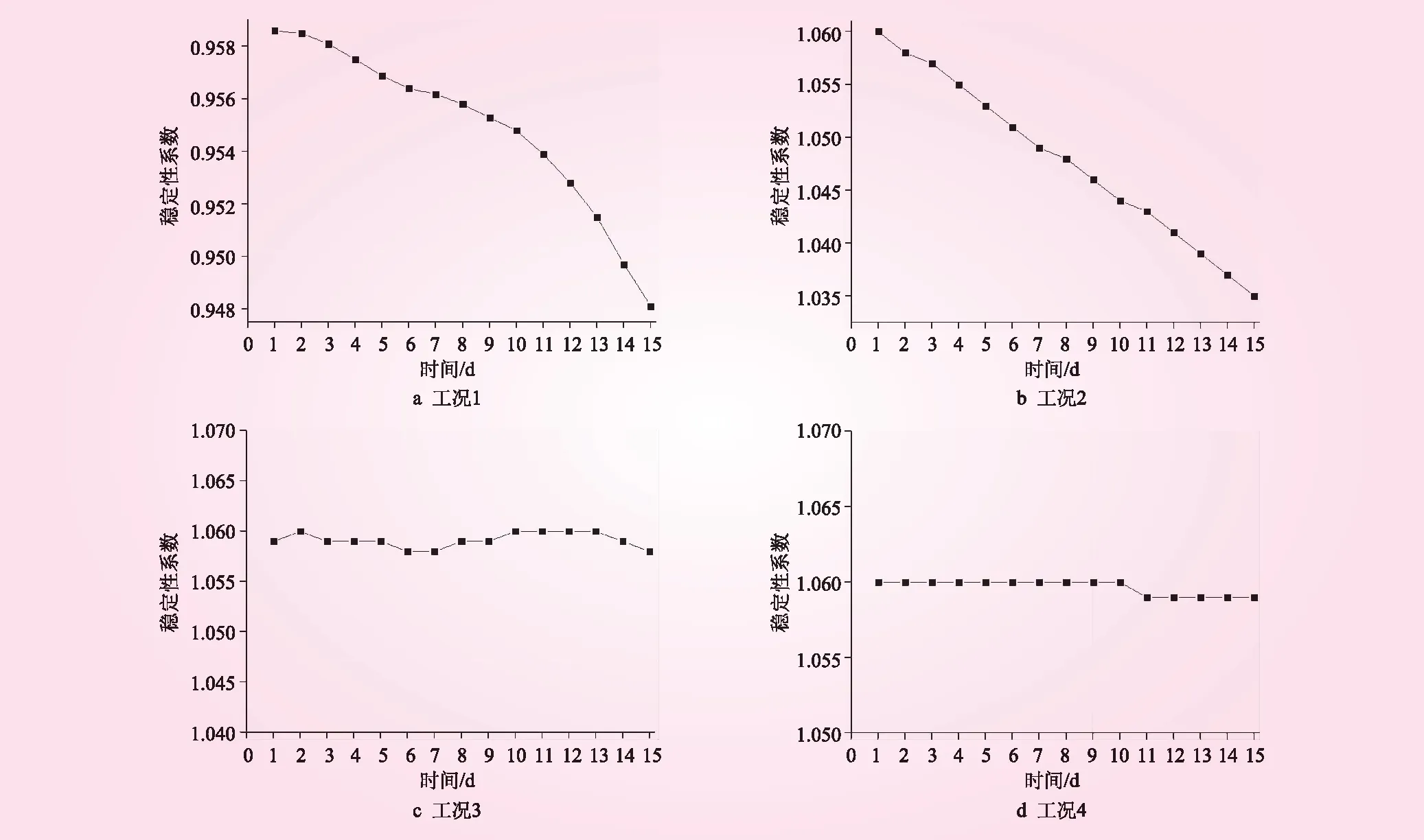
图5 不同工况下稳定性系数与时间的关系
不同工况下滑坡稳定性系数汇总见图6。从图6可知,在库水位相对较低降速时,在当前的降雨量情况下或未降雨时,对滑坡的稳定性影响作用不大,稳定性曲线基本持平;而在库水位相对较高降速时,稳定性才有明显的下降;对于无雨情况,其稳定性系数下降点基本与低降速时起点一致。而当相对较高降速和降雨耦合作用下,从第1 d后开始,就相对其他3种工况下的稳定性更低。
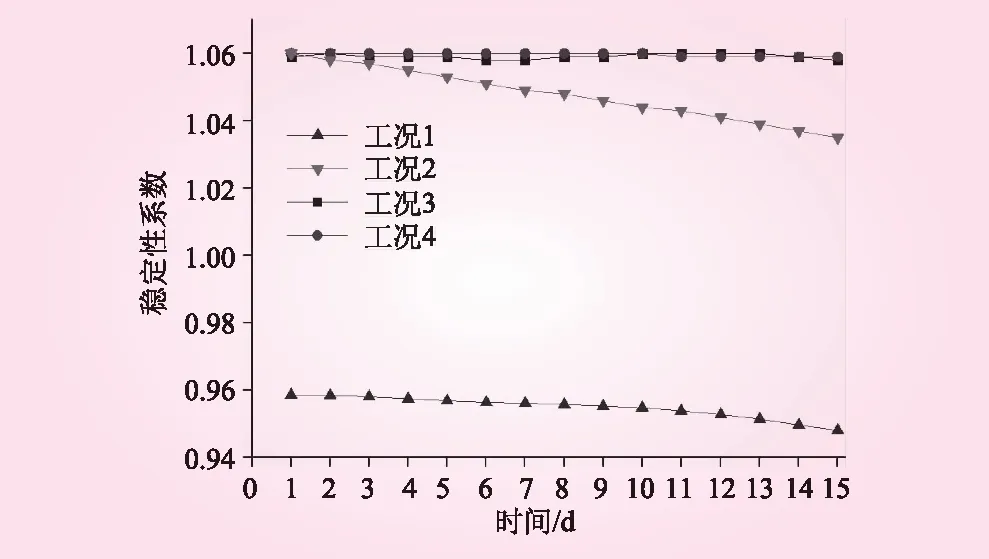
图6 不同工况下滑坡稳定性系数汇总
3.5 可靠度分析
按照点估计理论,将4种工况分别取平均数,由式(4)即得到4种不同的稳定性组合,即
F++=F(W+,R+)=0.955
F+-=F(W+,R-)=1.048
(12)
F-+=F(W-,R+)=1.059
F--=F(W-,R-)=1.060
(13)
经点估计理论,对安全系数加以简单、高效的计算。由式(5)得出稳定性系数均值为1.03,由式(6)得出稳定性系数标准差为0.044,由式(7)可靠度指标为0.693,由式(8)失效概率为24.41%。
根据三峡库区地质灾害防治工程地质勘察技术要求所规定的滑坡稳定状态分级(见表2)[11],该目前滑坡处于欠稳定阶段,也验证了易庆林等根据监测资料进行变形分析得出欠稳定的结论[2]。因此,通过点估计理论得出的评价指标也能得出相同的结论。

表2 滑坡稳定状态分级
注:Fst为滑坡稳定性安全系数。
工况1稳定性系数只有0.955,故在库水位相对较高降速和降雨情况下是最有可能滑动的。根据点估计理论得出的稳定性系数均值为1.030,虽然大于1,但可靠度不足0.7,失效概率为24.41%,应加强监测和巡查力度。
4 结 语
本文采用点估计法,基于库水位不同降速和有无降雨情况,计算了三门洞滑坡的稳定性,并进行可靠性分析,得出以下几个结论:
(1)库水位相对较低降速时,对滑坡的稳定性影响作用不大;而在库水位相对较高降速时,稳定性有明显的下降;对于无雨情况,其稳定性系数下降点基本与低降速时起点一致;而当相对较高降速和降雨耦合作用下,稳定性系数更低,也证实了三门洞滑坡为库水位下降-降雨型滑坡的结论。
(2)从可靠性分析计算中得出,三门洞滑坡稳定性系数均值为1.03,稳定性系数标准差为0.044,可靠度指标为0.693,失效概率为24.41%,具体的数值直观地体现了稳定性状况。其中,稳定性系数均值为1.03,可确定该目前滑坡处于欠稳定阶段。
(3)点估计理论为滑坡稳定性评价提供另一种评价指标,也验证了前人所得的结论,进一步说明基于点估计理论的可靠度分析在滑坡稳定性评价中的可靠性,可为涉水型滑坡的其他影响因素变量的选取研究建立基础,为滑坡的预测分析提供更加全面、科学、可靠的理论依据。

