近钻头电阻率测量理论及响应模拟

宋殿光,岳步江,狄帮让,范业活,贺明

(1.中国石油大学地球物理与信息工程学院,北京102249;2.航天科工惯性技术有限公司,北京100074;3.中国电波传播研究所,河南新乡453000)

0 引 言

随着越来越多的油气田被勘探开发,陆上浅层及浅海的油气资源已逐渐枯竭,中国油气资源呈现出整体分散、局部集中的分布,开发目标开始转向那些规模更小、油层更薄、裂缝油藏和物性差的油藏,这对成功钻遇油气层提出了更高的技术要求。地质导向技术在这样的大背景下得到快速发展,该技术通过井下传感器测量的地质及工程参数实时识别地下构造及属性信息,指导钻头顺利中靶及最大限度地在目的层中钻进。随钻电磁波电阻率及方位伽马仪器是目前地质导向应用最多的井下测量短节[1-6],但由于其距离钻头较远,在地层横向起伏较大、有断层存在时,经常出现当仪器识别出层界面时,钻头早已出目的层的现象。

因此,在地质导向应用中,近钻头测量[7-10]受到越来越多的青睐。针对侧向类近钻头电阻率的测量原理、响应特性进行了仿真模拟,可以为研制该类仪器提供一定的理论支持。

1 基本理论

1.1 工作原理

仪器发射和接收天线均为螺线环,将通电螺线环套在钻铤外,则螺线环上下端的钻铤上会产生感应电压,进而在钻铤中产生电流。电流沿着钻铤和周围的介质向外扩散,钻铤上分布电流的大小与周围地层电阻率的高低和非均质性相关,钻铤某处的电流可以利用测量该处接收螺线环天线上的电流得到,因此,通过测量接收螺线环天线上的电流,即可实现对钻铤周边电阻率信息的测量。

1.2 发射源的等效

由电流源Iin激励起的磁场HIinφ满足[12-13]

(1)

由Maxwell方程

Ein=-φjωμHinφ

(2)

令分布磁场电流Im为

Im=×Ein=

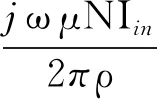
(3)

其中

(4)

总磁场电流IM为

IM=∬Imdρdz

(5)

则将式(3)代入式(5)可得

(6)

从上面的分析可知,通电螺线环可以采用磁流环的方式定量等效,进而方便在建模仿真时实现源的加载。

2 建模仿真分析

考虑到模型的复杂性,没办法用解析解进行分析,本文选择采用有限元仿真软件comsol[14-15]对仪器进行建模仿真。

2.1 2种等效源一致性的对比验证

根据螺线环与磁流源的等效关系,可以将模型简化为轴对称二维和三维模型,如图1、图2所示。2个模型的发射源均设置为单位磁流源,接收放置在近钻头测量位置处,测量该处的磁场强度。本文所有仿真,均采用该设置。

图1 轴对称二维磁流源模型

图2 三维磁流源模型

为验证2种等效模型的正确性,在1 Ω·m均匀地层模型中,分别对2种模型的响应进行仿真。将2种模型的所有参数设为相同,设钻铤内半径为0.05 m,外半径为0.085 725 m,钻铤总长25 m,天线与钻铤间距0.005 m,发射天线距离钻头端面1 m,分别计算钻头方向0.6、0.7、0.8、0.9 m源距和钻头反方向8、9、10、11、12 m源距下的接收磁场强度信号,结果见表1。

由于模型维数不同,受网格剖分精细度影响,两者结果会存在一定的误差。但从表1中看出,2个模型结果的差别最大为2.05%,最小为0.07%,总体上一致性很好,可以互相验证2个模型的正确性。

表1 不同源距下2种模型的结果比较

2.2 仿真结果与实验的对比验证

用实验方法对螺线环等效为磁流源模型进行验证。实验中,钻铤半径为0.05 m,螺线环天线半径为0.08 m,将钻铤和天线放入在地面挖出的狭长水槽中,水槽长10 m,水深约0.5 m,土壤及水的电阻率约为10 Ω·m。选择三维模型对实验装置的响应进行仿真,发射天线依然选择放在离钻铤端面1 m位置处,将接收天线放置在发射天线两侧不同位置,理论仿真得到的接收磁场强度值与实测螺线环上的电压值对比见表2、表3。

表2 钻头方向端接收信号随源距的变化关系

表3 钻头反方向端接收信号随源距的变化关系

由于螺线环输入电流不容易精确测得,则等效为磁流源的大小也无法精确得到,故仿真中设为单位磁流源。装置周围水电阻率与大地电阻率值用电阻率计测量得到。很明显,实验得到的螺线环上的电压值与该位置处轴向磁场强度具有定比例关系,因此可以将这两者进行比较分析,但由于发射源没法统一,故不能对两者进行直接比较。本文采取对不同位置处的计算值和测量值做归一化处理的方式,实现了对两者信号变化规律的比较。由于理论模型本身就是对实际模型的简化,再加上实际电路测量方面也会有一些误差,因此两者也必定会存在一定误差。从归一化的结果来看,两者的误差最大不超过3.6%,可以说明理论计算和实际测量具有很好一致性。

综上,通过2种仿真模型之间结果的对比,以及理论与实际结果之间的对比,可以充分说明所采用的物理仿真模型的正确性及适用性。

2.3 响应信号随电阻率的变化规律

为简化计算量,采用轴对称二维磁流源模型,令钻铤内半径为0.05 m,外半径为0.085 725 m,钻铤总长25 m,电阻率测量源距为0.6 m,测量天线距离钻头端面0.4 m,天线与钻铤间距0.011 m,计算频率分别为1 kHz和2 kHz时,近钻头测量信号(指磁场强度,后面算例中,无特别说明,均同此意)随地层电阻率的变化关系曲线见图3。

图3 测量信号随电阻率的变化关系

2.4 钻铤与天线间距对信号的影响

采用与2.3节相同的模型参数,在0.1 Ω·m地层下,计算1 kHz和2 kHz时,天线与钻铤间距从0.011 m变化到0.05 m时的信号变化,曲线见图4。从图4可见,2种频率下,近钻头信号都随间距的增大而减小,但减小的幅度不大,且间距的变化不影响频率对信号的影响规律。改变地层电阻率,规律不变。

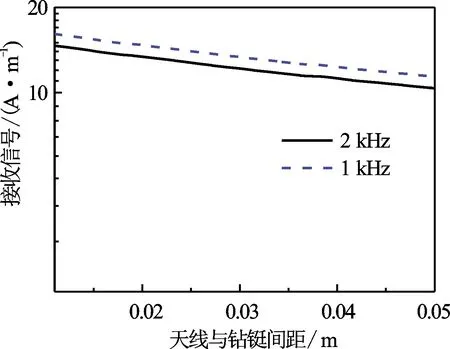
图4 天线与钻铤间距变化对信号的影响关系

2.5 探测深度分析

仪器模型同2.3节,频率选为1kHz,模拟仪器穿过地层界面的曲线特征(见图5),地层对比度为50∶1。从图5可见,距离界面1 m以外信号变化幅度很小,0.5 m内变化明显。将50 Ω·m地层的信号作为信号基值,计算出其他深度处信号相对于该基值的变化率(见图6)。从图6可见,如果以仪器信号变化2%作为预判前方有地层界面,则探测深度为1 m;如果以仪器信号变化5%为依据,则探测深度为0.67 m;如果以信号变化10%为依据则探测深度为0.5 m。

图5 仪器穿过地层界面时的变化曲线

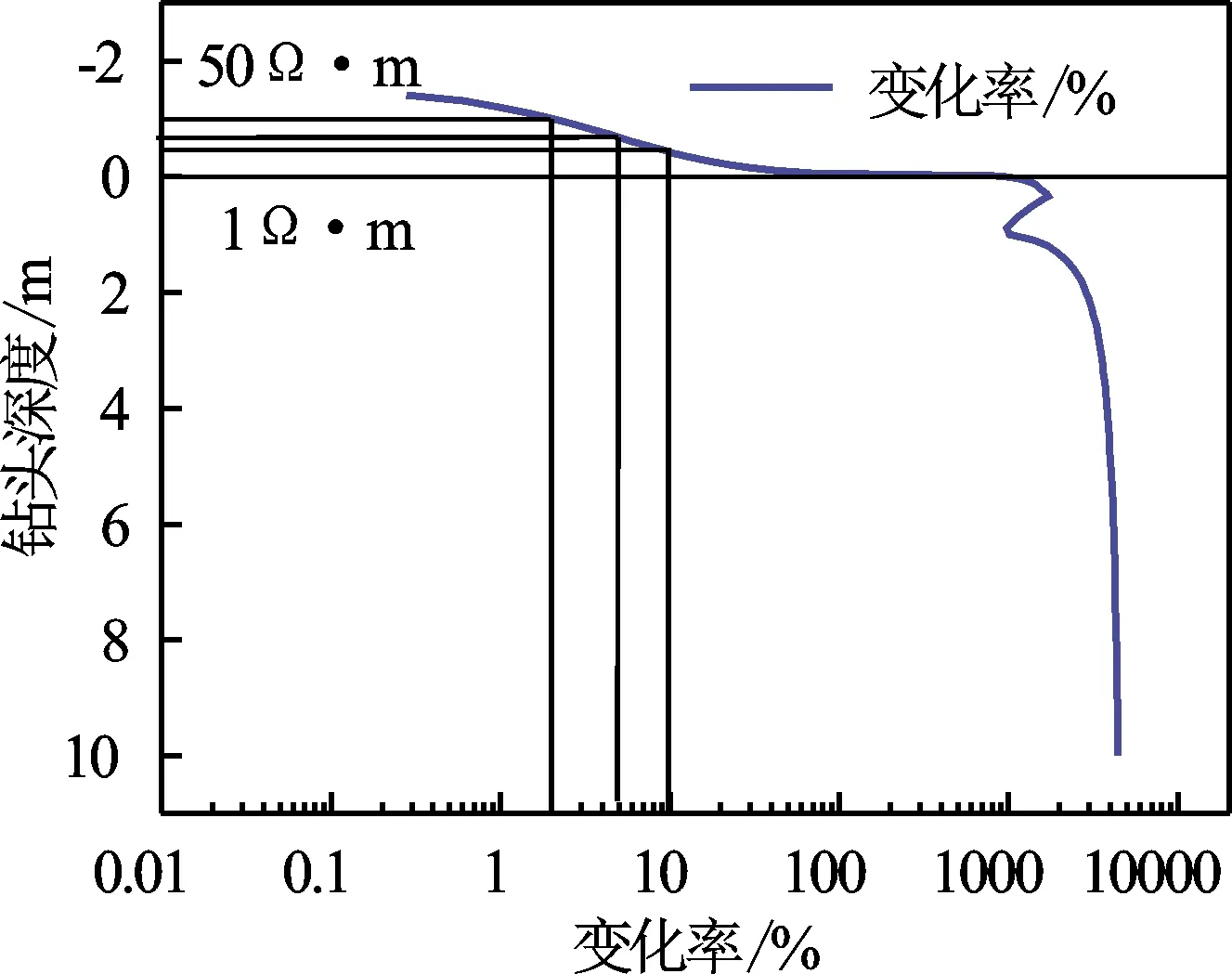
图6 信号变化率同仪器距边界距离的关系

仪器径向探测深度特性模型无法用轴对称二维简化,因此采用三维磁流源模型。图7为磁场信号随距离d的变化,同样将50 Ω·m的信号作为基值,绘制不同深度处信号相对于该基值的变化率曲线(见图8)。从图8可见,如将信号变化2%作为探测到地层边界的依据,则钻头电阻率的径向探测深度为2.5 m;如果以5%作为依据,则探测深度为1.15 m;如以10%为依据,则探测深度为0.7 m。

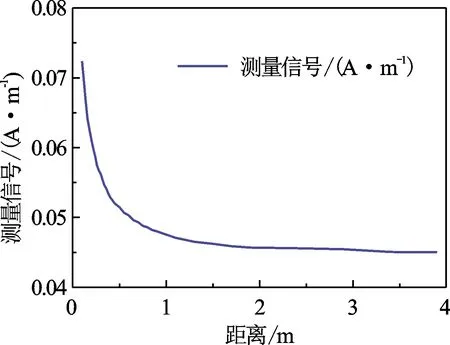
图7 响应随距离的变化曲线

图8 信号变化率同仪器与边界距离的关系

2.6 纵向分辨率特性分析

为考察仪器的分辨率特性,模拟了仪器垂直穿过一系列薄层的响应,选择层厚分别为0.012 7、0.025 4、0.050 8、0.076 2、0.152 4、0.304 8、0.61、1.219 2、2.438 4 m,目地层与围岩电阻率对比度分别选为10∶1和1∶10,仪器模型同2.3节,频率为1 kHz,采用轴对称二维模型,模拟曲线见图9、图10。可见,当目的层与围岩电阻率为10 Ω·m和1 Ω·m时,近钻头电阻率能分辨出0.3 m左右的地层;当目的层与围岩电阻率为1 Ω·m和10 Ω·m时,钻头电阻率分辨能力能达到0.15 m。说明该仪器分辨低阻层的能力要强于高电阻率层。

图9 10∶1地层近钻头电阻率曲线

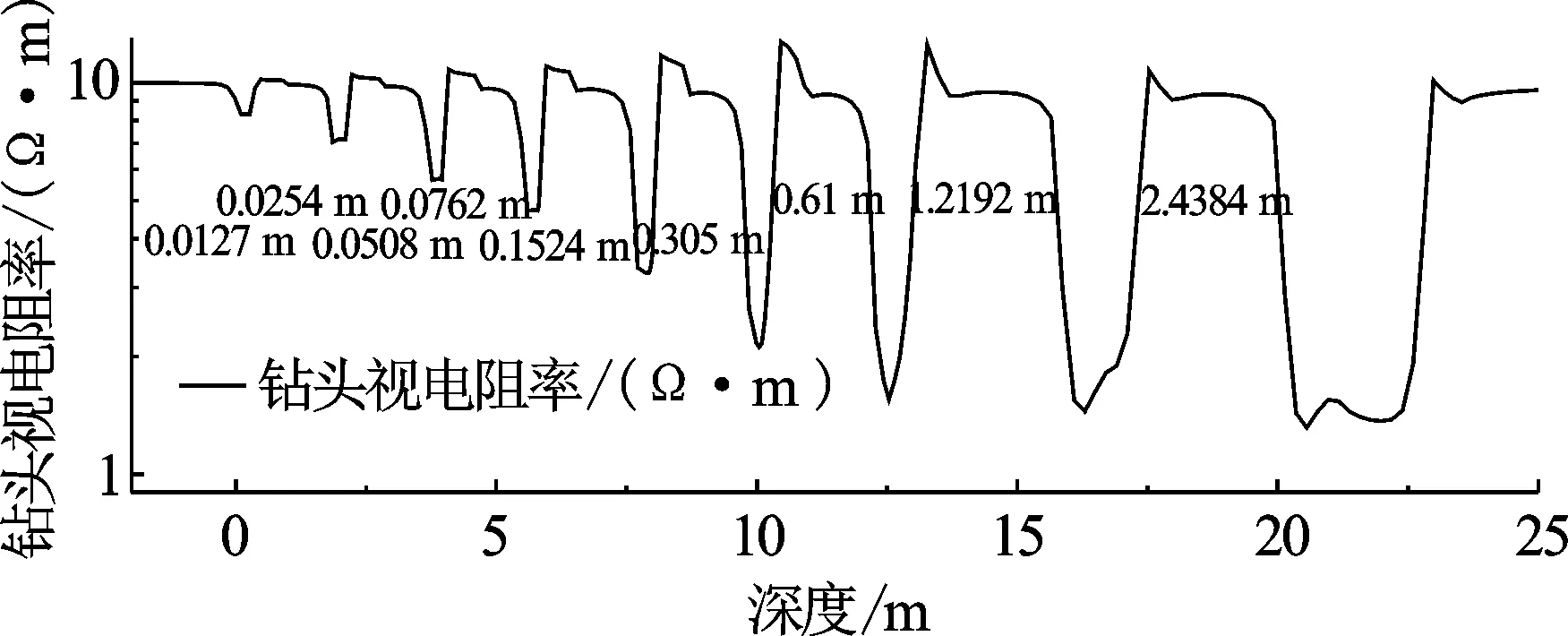
图10 1∶10地层近钻头电阻率曲线

3 结 论

通过对螺线环天线进行等效变换,利用comsol有限元仿真软件对近钻头电阻率仪器建立了轴对称二维和三维磁流源物理模型。通过2种模型间的结果对比和数值模拟与实验结果的对比,验证了2种磁流源等效模型的正确性及有效性。同时利用这2种模型对仪器的探测特性进行了仿真分析,得到了一些有价值的结论,对研制该类仪器及分析该类仪器的响应特性具有一定的借鉴意义,结论如下。

(1)采用通电螺线环作为发射源的近钻头测量,在仿真中可以将发射源等效为环形磁流源。

(2)在源距为0.6 m、接收位置距离钻头端面0.4 m、工作频率为1 kHz时,接收信号与地层电阻率呈线性反比关系,适当变化频率及源距,规律不变,因此可以通过刻度系数k实现视电阻率的转换。

(3)随着天线与钻铤间距的增大,测量信号变小,但变化幅度较小。因此,在设计仪器结构式,可不必过分考虑间距对信号的影响。

(4)按照本文仿真采用的结构尺寸计算,按信号变化10%作为探测到地层边界的依据,则仪器沿钻头前方向的探测深度为0.5 m,径向探测深度为0.7 m。可见,该仪器径向探测能力稍优于向前探测能力,有很好地识别钻头周边地质环境的能力。

(5)按照本文仿真采用的结构尺寸计算,该仪器的纵向分辨能力在目的层与围岩电阻率为10 Ω·m和1 Ω·m地层中约为0.3 m左右,在目的层与围岩电阻率为1 Ω·m和10 Ω·m的地层中分辨能力变高,可以达到0.15 m左右。