基于元素测井的束缚水饱和度计算方法

李鹏

(中海油田服务股份有限公司,天津300459)

0 引 言

束缚水饱和度是储层测井评价的重要参数之一,其主要依赖岩心实验分析获取,但岩心成本较高,且不连续,因此采用测井技术开展束缚水饱和度研究是解决束缚水饱和度评价的常用方法。束缚水饱和度在岩心实验分析过程中影响因素[1-2]较多,使得束缚水饱和度精度往往在一个区间范围[3],同时由于储层类型不同,其对束缚水饱和度影响因素[4]差异较大,不同测井方法计算的束缚水饱和度也存在一定差异。

目前,获取较为准确的束缚水饱和度方法主要包括毛细管压力实验[5]、核磁共振实验[6-7]或压汞与核磁共振联测[8]等,通过驱替的方法获取一定压力下岩心的束缚水饱和度,而测井资料计算束缚水饱和度方法相对较多。刑会民[9]通过常规测井计算钻井液侵入进行束缚水饱和度计算,由于侵入难以准确计算,使得束缚水饱和度计算精度相对较低。苏俊磊等[10]通过变T2截止值的方法确定束缚水饱和度,但变T2截止值方法不统一,划分的孔隙空间差异较大。陆云龙等[11]通过混合液电阻率反演确定束缚水饱和度,但钻井液矿化度与地层水矿化度要有较大差异。付晨东[12]通过T2谱组分建立模型计算束缚水饱和度,然而受流体性质影响,T2谱差异较大,对束缚水饱和度影响较大。常俊等[13]通过统计回归计算束缚水饱和度,受地区影响较大,难以推广应用。

元素测井通过测量地层元素含量进而计算矿物含量,实现地层岩性识别[14]。近几年在孔隙度、渗透率评价中取得较大进展,通过岩心标定能够得到较为精确的储层渗透率参数。本文基于元素测井获取的渗透率,根据Coates-Timur[15-16]公式建立新的束缚水饱和度模型,通过线性多元回归采用岩心标定精确计算束缚水饱和度,在渤海油田多种疑难层测井解释中发挥了较大作用。

1 元素测井渗透率计算方法

研究表明,储层渗透率与岩石颗粒表面积、孔隙体积、孔隙喉道有关,对于简单孔隙几何因子地层,地层渗透率与孔隙表面积同孔隙体积之比成反比[17-18]。孔隙表面积与孔隙体积之比,则与岩石矿物成分、骨架密度及颗粒比表面积有关,因此建立关于孔隙度、骨架密度、矿物成分与颗粒比表面的渗透率模型,即k_Lambda渗透率模型

(1)

式中,K为元素测井计算的渗透率,mD(1)非法定计量单位,1 mD=9.87×10-4 μm2,下同;φ为孔隙度,%;a为常数,无量纲;ρm为骨架密度,g/cm3;Mi为矿物含量,%;A0i为矿物的比表面积,m2/g;vi为矿物校正系数,无量纲。

实验分析[19]表明,不同矿物成分其比表面积不同但数值较为固定,同时考虑到并非每种矿物成分的所有比表面积都参与到流体流动,因此采用校正系数对不同矿物比表面积的渗透性贡献值进行校正,得到合理的比表面积。黏土矿物比表面较大,但权重相对较低,对渗透率贡献较小。

元素测井能够提供准确的地层矿物成分含量与骨架密度,结合常规测井计算的孔隙度、岩电分析的胶结指数,通过地区岩心刻度即可实现渗透率精细计算。

2 束缚水饱和度模型及参数确定

Coates-Timur模型为经典渗透率经验模型,用于描述储层渗透率、孔隙度、束缚水孔隙与可动水孔隙之间的关系,通常用于渗透率参数的定量计算,其公式如下

(2)

式中,K为渗透率,mD;φb为束缚流体孔隙度,%;a、b、c为常数,无量纲。

由式(2)可以推导出束缚水饱和度与渗透率、孔隙度之间的关系

(3)

式中,Swi为束缚水饱和度,无量纲。

对式(3)两边取对数,结果如下

(5)

(6)

式中,a′、b′、c′为常数,无量纲。

(7)

3 应用效果分析

实例1:复杂岩性储层束缚水饱和度计算。图1为渤海中部海域石臼坨凸起东段Q4井岩心分析孔渗关系及测井渗透率评价效果图。Q4井目的层段为沙河街组,地层岩性为混积岩,主要岩性包括灰质砂砾岩、鲕粒白云岩、白云质砂岩、砂砾岩、凝灰质砂岩等,储集空间以次生溶蚀孔隙和粒间孔为主。受岩性差异影响,储层物性差别大、非均质性强,岩心孔渗关系杂乱,无法用常规孔渗关系定量计算储层渗透率[图1(a)]。 通过元素测井计算的矿物含量,

图1 石臼坨凸起复杂岩性储层Q 4井渗透率评价效果图*非法定计量单位,1 ft=12 in=0.304 8 m,下同

图2 Q 5井束缚水饱和度计算效果图

根据式(1)对该井渗透率进行计算可以发现,复杂岩性储层元素测井计算的渗透率与岩心分析渗透率基本吻合,变化趋势一致,计算精度较高。

通过Q4井取心段岩心分析数据选取不同物性对应的实验参数(见表1),对式(6)进行多元线性回归拟合,得到该区束缚水饱和度计算公式,相关性达到0.73,其中a′、b′、c′常数分别为0.62、1.05、0.13。通过该公式对石臼坨凸起东段Q5井进行计算,采用Q5井元素测井计算的渗透率,结合常规测井计算的孔隙度,得到Q5井束缚水饱和度值,并将计算结果与Q5井岩心分析束缚水饱和度进行对比(见图2)。可以看出,通过式(7)计算的束缚水饱和度与岩心分析束缚水饱和度吻合较好,而常规电阻率测井曲线受岩性影响,储层发育段电阻率值较低,非储层段电阻率值较高,基于阿尔奇公式的传统饱和度模型难以准确计算储层含水饱和度,因此通过元素测井能够较好地解决复杂岩性储层饱和度计算难题。

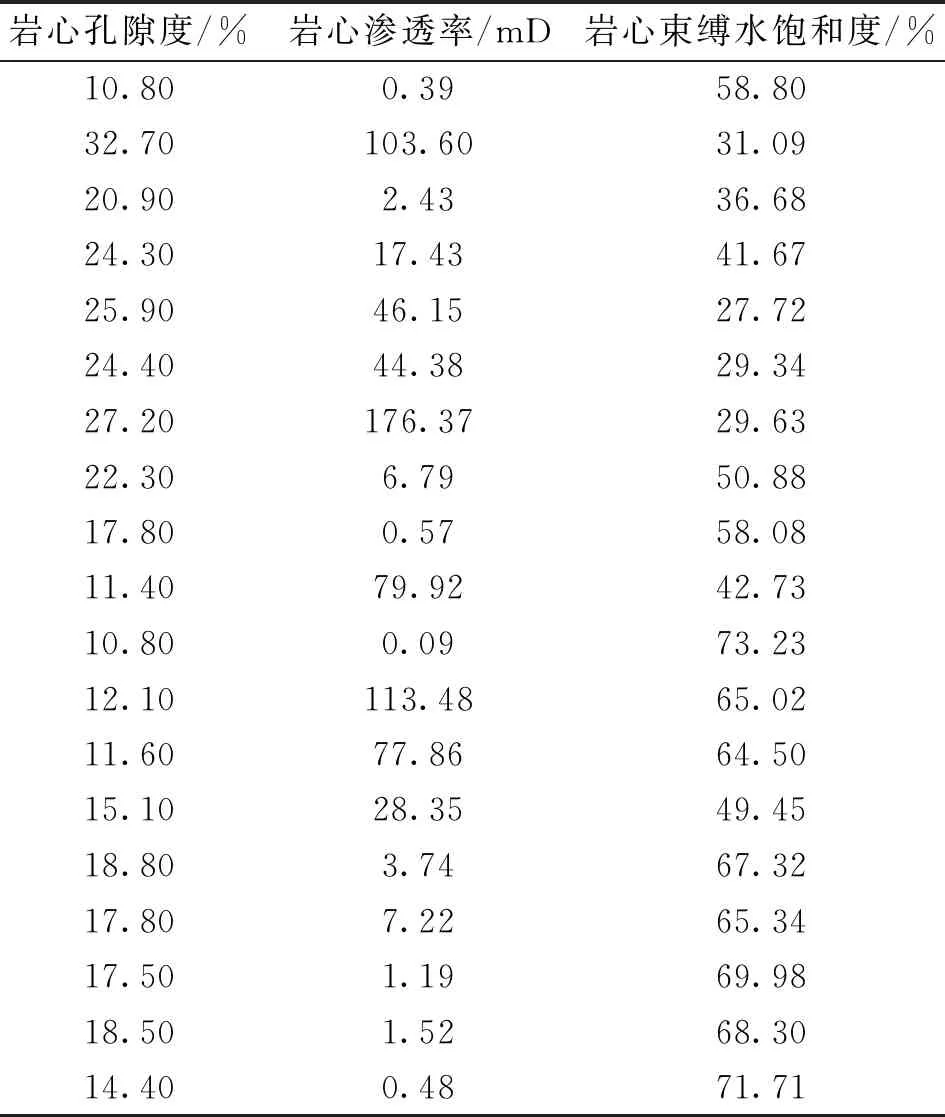
表1 Q 4井孔隙度、渗透率、束缚水饱和度岩心分析结果

实例2:水淹层定量评价。SZ油田为渤海开发较早的油田,采用注水开发,目前面临水淹问题,是渤海典型的高含水油田。该油田以水平井生产为主,水平段水淹层测井解释成为水淹层判别的主要手段。图3为该油田C34井通过束缚水饱和度计算进行水淹层测井解释效果图。从图3可见,水平段自然伽马值较低(第1道红线),主要钻遇砂层,井轨迹呈现“W”型(第1道黑线)。采用式(6)～式(7)计算水平段的束缚水饱和度(第6道黑线)与常规测井基于阿尔奇公式计算的当前储层含水饱和度(第6道红线)的对比可以看出,2 083.0～2 130.0 m井段两者差异明显,同时电阻率值较低(第4道),钻遇砂层部位较低(第1道黑线),解释为水淹层;2 130.0～2 240.0 m井段束缚水饱和度与常规测井解释含水饱和度基本重叠,且电阻率值较高,解释为未水淹。该井投产初期日产油60.0 m3,含水56.0%,1个月后含水上升到70.0%,证实水淹层解释较为合理。

图3 SZ油田C34井水淹层定量解释效果图

图4 QHD油田低电阻率油层饱和度计算效果

实例3:低电阻率油层饱和度计算。渤海油田发育大量低电阻率油层,其储量占比较大,图4为渤海QHD油田明化镇组低电阻率油层测井响应特征及束缚水饱和度计算效果图。从图4可见,常规油层电阻率值通常大于10.0 Ω·m,1 090.0～1 098.0 m、1 108.0～1 120.0 m井段电阻率值小于10.0 Ω·m,自然伽马相对较高,储层物性相对较差,为典型的低电阻率油层。采用式(6)～式(7)计算的束缚水饱和度在常规油层段(1 120.0～1 133.0 m)与低电阻率油层段(1 108.0～1 120.0 m)均与岩心分析束缚水饱和度吻合较好,因此计算的束缚水饱和度成为低电阻率油层饱和度计算的一项有效方法。

4 结 论

(1)提出基于元素测井束缚水饱和度计算方法,扩展了元素测井应用范围,是束缚水饱和度计算的一种有效方法。

(2)通过对Coates-Timur模型进行转换,得到束缚水饱和度计算模型,采用多元线性回归确定模型参数,使得方法适用于不同类型油田。

(3)基于元素测井的束缚水饱和度计算方法对复杂岩性储层、低电阻率油层饱和度计算应用效果较好,在水淹层定量判别中作用明显,值得推广应用。