一类具有强奇性的矩阵型偏微分方程的正解的存在性*

双 震，孙义静

(中国科学院大学数学科学学院， 北京 100049)

本文研究一类具有强奇性的矩阵型偏微分方程。

(1)

其中Ω⊂Rn是有界开集,M(x)是Ω上实对称矩阵, 满足存在正常数α,β使得M(x)ξ·ξ≥α|ξ|2,|detM(x)| ≤β,∀ξ∈Rn,∀x∈Ω, -p<-1, 00 a.e. in Ω,λ>0是参数。

1 本文的结论

(2)

注: 在定理1.1和定理1.2中, 要求Ω具有光滑边界, 实际上只要Ω具有锥性质就足够了。 因为只需要保证Sobolev嵌入定理成立, 具体可见文献[12]。

(3)

(4)

(5)

2 定理的证明

先介绍一些引理。

引理2.1设M(x)是定义Ω上实对称矩阵, 满足存在正常数α,β使得M(x)ξ·ξ≥α|ξ|2,|detM(x)| ≤β,∀ξ∈Rn,∀x∈Ω, 则

∀x∈Ω,∀ξ,η∈Rn.

(6)

证明固定x∈Ω。 因为M(x)是实对称矩阵, 所以存在正交矩阵Q(x)使得

其中λi(x),i=1，…，n是矩阵M(x)的特征值, 且λi(x)≥α>0,i=1，…，n, 这是因为λi(x)是M(x)的特征值, 所以存在x0≠0, 满足M(x)x0=λi(x)x0, 从而α|x0|2≤M(x)x0·x0=λi(x)x0·x0=λi(x)|x0|2, 故λi(x)≥α,i=1…n。

对任意ξ,η∈Rn, 令x=QTξ,y=QTη, 则Mξ·η=xQTMQy=λ1x1y1+λ2x2y2+…+λnxnyn, 故

因为|x|2=xTx=(QTξ)TQTξ=ξTQQTξ=ξTξ=|ξ|2, 同理|y|2=|η|2。

□

证明根据M(x)的性质和引理2.1, 可以得到

(7)

(8)

结合式(7), 可推得

‖u+v‖1≤‖u‖1+‖v‖1.

□

引理2.3N1是闭集。

从而

(9)

所以u∈N1。 因此N1是闭集。

□

则存在唯一的t0=t(u0)>0, 使得

1)I(t(u0)u0)≤I(tu0) ∀t>0, 即在t(u0)点达到最小值；

2)t(u0)u0∈N2。

(10)

容易看出dI(tu0)/dt在(0,+∞)内有唯一零点, 记为t(u0)=t0, 而且在区间(0,t0)内dI(tu0)/dt<0, 在区间(t0, +∞)内dI(tu0)/dt>0, 说明I(tu0),∀t>0在(0,t0]单调递减, 在[t0,+∞)单调递增, 所以I(tu0),∀t>0在t0处取得最小值, 从而式(1)成立。 另外还可得到

(11)

所以t(u0)u0∈N2。

□

引理2.5泛函I在N1中下半连续。

(12)

同引理2.3中的证明，由Fatou引理可知对ui的一个子列成立(仍记为ui)

□

引理2.6存在常数C0>0，使得∀u∈N1,‖u‖≥C0。

证明设u∈N1, 则

由反向 Hölder不等式和 Poincaré不等式可以得到

从而可以得到

‖u‖≥C0.

(这里C0与Ω,β,α,p,f(x)有关。)

□

□

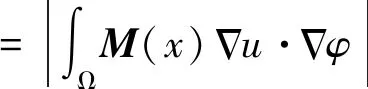
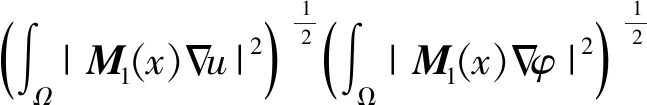
接下来开始定理1.1的证明。

定理1.1的证明由引理2.3, 2.4和2.5, 可知N1是闭集,N1非空,I在N1上有定义而且下半连续。 因为∀u∈N1有

(13)

所以I在N1上有下界。 从而根据Ekeland变分原理, 可取最优化极小值序列, 即存在序列{ui}⊂N1, 使得

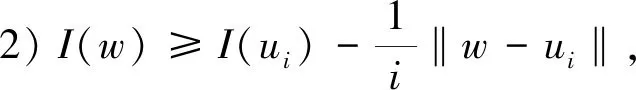
(14)

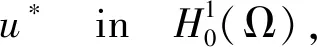
(15)

(16)

ui(x)→u*(x) a.e.in Ω.

(17)

下面需要分两种情况讨论。

情况1{ui}中有一个子列位于N2内(下面仍把这个子列记为ui)。

根据引理2.4，可知存在唯一的正实数, 记为fi,φ(t), 满足

下面证明fi,φ(t)在t≥0上连续。 记

(18)

任取t0∈[0,+∞), 考虑函数

能够得到f(x)在(0,+∞)内严格递增且在(0,+∞)内有唯一零点, 即fi,φ(t0)。 从而fi,φ(t)在t≥0上连续。

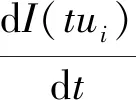
定义

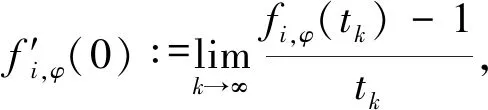
从而利用-p<-1,ui>0,t>0,φ≥0,f>0, 知

(19)

其中o(1)表示当t→0+时的无穷小。 利用控制收敛定理可以证明当t→0+时,

利用前面4个函数的连续性以及ui∈N2, 在式 (19)两边令t→0+可得到

(20)

根据式 (14)中的第2个结论以及fi,φ(t)(ui+tφ)∈N2,有

I(ui)≤I(fi,φ(t)(ui+tφ))+

代入计算, 因为ui∈N2, 得到

从而有

在上式中令t→0+,

(21)

由引理2.6和ui∈N2可以得到,

由于{ui}有界, 所以

从而可知存在N∈N*, 当i>N时有

(22)

∀i>N.

根据式 (14)中的第2个结论以及fi,φ(t)(ui+tφ)∈N2, 有

其中o(1)表示当t→0+时的无穷小。 在上式中令t→0+取下极限, 因为ui∈N2, 可知

(23)

另一方面，由Fatou引理可以得到

(24)

由式(17)用Fatou引理, 并结合式(23)和式(24), 可得

(25)

(26)

(27)

由式 (14)中第1个结论和式(16)可得

(28)

式(28)中还用到了引理2.4和下面两个结论。

1)由式(15)和引理2.2可知

2)由式(17)和Fatou引理可知

由式(28)可以得到I(u*)=I(t(u*)u*), 根据引理2.4中的最小值的性质可知t(u*)=1, 从而u*∈N2。

情况2对充分大的i有ui∈N1N2。

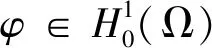
因为ui∈N1N2, 所以

由g(t),h(t),k(t)的连续性可知, 当t充分小时成立

即得ui+tφ∈N1N2.

代入计算, 两边同除以t得

令t→0+取上极限(通过引理2.7和式(15)), 得到

(29)

另外由ui(x)→u*(x) a.e.in Ω,利用Fatou引理可得

(30)

(31)

结合式(29),式(30)和式(31)可知

所以

所以u*∈N2.

无论是情况1还是情况2都得到这样的结果,

(32)

两边除以t, 令t→0+, 其中meas{u*+tψ<0}→0, 可知

(33)

从而

(34)

即说明u*是方程 (1)的弱解。

□

定理1.2是运用定理1.1的结论的一个例子。

定理1.2的证明设φ1是-Δ在Dirichlet边界条件下的第一特征向量, 即

而且在Ω内φ1>0, 其中λ1表示-Δ在Dirichlet边界条件下的第一特征值。

∀x∈Ω.

(35)

根据定理1.1即得要证结论。

□