易燃液体闪点预测模型综述

景冬莲 ，俞 英 ，商 杰 ，黄海燕 *

（1.中国石油大学（北京）理学院重质油加工国家重点实验室，北京 102249；2.广西出入境检验检疫局危险品检测技术中心，广西 南宁 536008）

闪点是衡量可燃液体火灾危险性的重要参数，在石油化工领域，生产、使用和储存有机物的场所均涉及危险等级的划分，而危险等级的划分以及相应的处理措施都取决于液体的闪点。闪点的实验测定方法有开口杯法和闭口杯法，是获得闪点数据的有效方法。但由于有机化合物数目众多，结构复杂，完全依靠实验方法测定，其工作量是十分巨大的，甚至是不可能的；其次，实验方法影响因素众多，实验结果差别较大，且费时费力；更重要的是，对于有毒、易挥发、易爆和放射性化合物，实验测试难度很大，有的根本无法通过实验进行测定。少数纯物质的闪点可以查阅化学品安全技术说明书，但不能满足闪点数据的大量需求。因此，探讨化合物闪点的预测方法具有重要的理论意义和实用价值。

本研究讨论了易燃物质的闪点预测方法，主要基于沸点，基团贡献和分子结构特性进行拟合预测。通过总结各种计算关联式和预测模型，也讨论了三种不同方法各自的优势和不足，以及特点和发展。

1 闪点预测方法及其发展

1.1 经验关联计算闪点

经验关联性为预测闪点Tf提供了最简单的方式，在可用的闪点预测关联性中，通常使用正常沸点Tb（NBP）、密度、蒸气压、临界性质和标准汽化焓（ΔHv）作为输入变量来预测闪点Tf，因为它们都代表化合物的挥发性[1]。

Bodhurtha[2]提出了最早的闪点预测的线性关联式(1)。该式适用于对烃类物质的闪点进行估算，估算值与实验值基本吻合。

式中:Tf-闪点，℃；Tb-沸点，℃。

王克强等人[3]采用拓扑化学方法，计算机建立了1457种有机化合物的闪点预测模型，如式(2)所示，其计算结果与实验数据符合较好，平均绝对误差11.96K，平均相对误差为3.75%，原理直观，方法简单，计算过程容易，但误差较大。

也有学者[4-6]提出了闪点Tf和正常沸点温度Tb之间的非线性关系式以及 Affen[7]、Butler[8]、Prug[9]、Hshieh[10]等不同计算方法。Affen方法[7]适用于正烯烃闪点的计算；Butler方法[8]分别对烷烃、醇、醛、胺和酮的闪点进行关联；Hshieh[10]预测一般有机化合物和有机硅化合物的闪点。显然，这些关联计算仅适用于特定类型的化合物，其应用范围受到一定限制。

Catoire和Naudet[13]以600个化合物的数据集提出了闪点Tf、正常沸点Tb，标准汽化焓ΔHv和碳原子数（n）之间的非线性关系，如式(3)所示，平均绝对偏差为6.36K，平均相对误差为1.84%。Gharagheizi等人[14]利用正常沸点和碳数得到经验关联式来预测1471种有机化合物闪点，其平均绝对偏差为2.4%，相关系数为0.979。

式中:ΔHv-标准汽化焓，kJ/mol；n-碳原子数。

高礼久等人[15]引入路径数Pn（反映分子的支化度）、路径数P3（极化数，用以表征分子的形状）、沸点(Tb)与C2～C20的烃类化合物(77种烷烃和烯烃)的闪点(Tf)进行相关分析。该模型的原理简单，方法实用，结果可靠，其预测值与实验值吻合良好，且置信度高达99.9%。但是路径数的引入比较繁琐。冯李立等人[16]设计了一个基于BP(Back-Propagation)算法的多层前馈网络模型，用于预测有机物闪点。以有机物沸点作为输入参数，闪点作为输出参数，共210种有机物作为实验样本，结果闪点预测值与实验值符合较好，其绝对平均相对误差为3.39%，小于沸点关联式法的绝对平均相对误差4.97%。

闪点的经验关联模型需要与相应物理性质如沸点、密度和汽化焓进行关联，通过关联式可以直观方便地得到有机物的闪点，便于理解，计算简单。

1.2 基团贡献法计算闪点

基团贡献法被广泛用于预测和估计纯有机物和混合物的热力学和其他性质。早期，Joback和Reid等人[17]根据基团贡献法（GCM），认为构成一个分子的官能团对所需的性质有线性或非线性的贡献，提出了一个最简单的模式称为Joback法。Dai等人[18]提出了一种基于基团贡献的多元线性回归方法来估计酯化合物的闪点。预测的80个酯的数据集的闪点与实验值有很好地一致性。得到的结果显示实验值的平方相关系数（R2）为0.9902，均方根误差为5.371K，平均绝对相对偏差为1.22%。

王克强等人[19]根据分子结构的特点，发展了一种预测有机化合物闪点的普适方法—三参数基团贡献法。将各类有机化合物的基团划分为50种基团，对750种有机化合物进行计算。结果表明，平均误差4.71%。闪点Tf的关联式为:

式中:ni为基团 i的数目，Δ(0)、Δ(1)和 Δ(2)为基团参数，xi=ni/∑nj为基团分率。该方法根据分子中基团的种类和数目预测化合物的性质，特点是基团划分简单易行、适用范围广，不足之处是对分子结构尤其是同分异构体的区分能力相对较差，预测精度不能令人满意。

Rowley等人[20,21]完全基于结构基团贡献开发了一种估算1062种有机化合物闪点的相关方法。Wang等人[22]通过结构基团贡献方法提出了有机硅化合物闪点的预测模型，建立的GCM模型包括39个贡献基团，是一个2阶多项式模型。Jia等人[23]使用GCM-MNLR模型（二阶基团贡献）预测了287种纯有机化合物的闪点，共计90个功能基团，其中76个二元基团，14个校正因子，其相关系数为0.9931，总绝对平均偏差和误差分别为3.77K和1.16%。Mathieu[24,25]基于 CH3-，-CH2-，>CH 和>C<四个结构基团的贡献，使用简单的代数表达式同样获得了92个烷烃的相同数据集的较好结果，相关系数为0.99，绝对平均偏差为4.12K。

Albahri等人[26,27]采用多元非线性回归（MNLR）和人工神经网络（ANN）两种方法确定闪点。模型的输入参数是37个结构基团在每个分子中出现的次数，传统的MNLR方法使用最小二乘法（R=0.90），ANN模型显著提高相关系数 （R=0.9961），ANN仅从分子结构预测纯化合物的闪点，总平均和最大误差分别为1.12%和6.62%。潘勇等人[28]建立了一个基于误差反向传播(Back-Propagation,BP)神经网络方法的基团贡献模型，优于传统基团贡献法所得结果。考虑到同分异构效应，Pan等人[29，30]利用基团贡献法建立了一种反向传播的9-5-1神经网络模型，对92个烷烃进行建模。虽然模型的准确度足够高，相关系数为0.99，绝对平均偏差为4.8K，但是它是基于少量分子开发的，这限制了它仅适用于烷烃。

Alibakhshi等人[31,32]提出了基于Joback基团贡献和正常沸点的模型来预测1533种有机化合物的闪点，平均相对偏差和平均偏差分别为1.61%和5.83K；Serat等人[33]提出了用分子结构和正常沸点作为输入信息的非线性基团贡献模型，该模型平均相对偏差和平均偏差为1.22%和5.7K。

基团贡献法在分子官能团与物质性质之间建立联系，通过此方法，利用分子结构即官能团组成就可预测有机物闪点等性质，为未知有机物的性质预测提供一定的帮助。

1.3 基于分子结构的闪点预测模型：定量结构-性质关系（QSPR）技术

近年来，定量结构-性质关系（QSPR）已经成为一个重要的方法，被广泛用于预测有机化合物的理化性质。典型的QSPR研究流程如图1所示。

图1 QSPR研究流程图

相比其他参数关联法及基团贡献法等理论预测方法，QSPR方法具有以下明显的优越性[34]:(l)仅根据分子的结构就能实现有机物性质的理论预测；(2)所获得的预测模型以具有明确物理化学意义的理论描述符作为输入参数，有助于找出与所研究的性质密切相关的结构因素，同时便于探索这些结构因素对性质的影响规律；(3)模型的输入参数较少，保证了模型的稳定性，便于计算处理，适用范围广，普适性强。

QSPR利用基于结构的物理量作为分子描述符来预测性质。在许多可用的描述符中，筛选出最有效的描述符，并通过数学关联或ANN来预测闪点，表1列举了使用不同描述符得到的QSPR模型的预测结果。

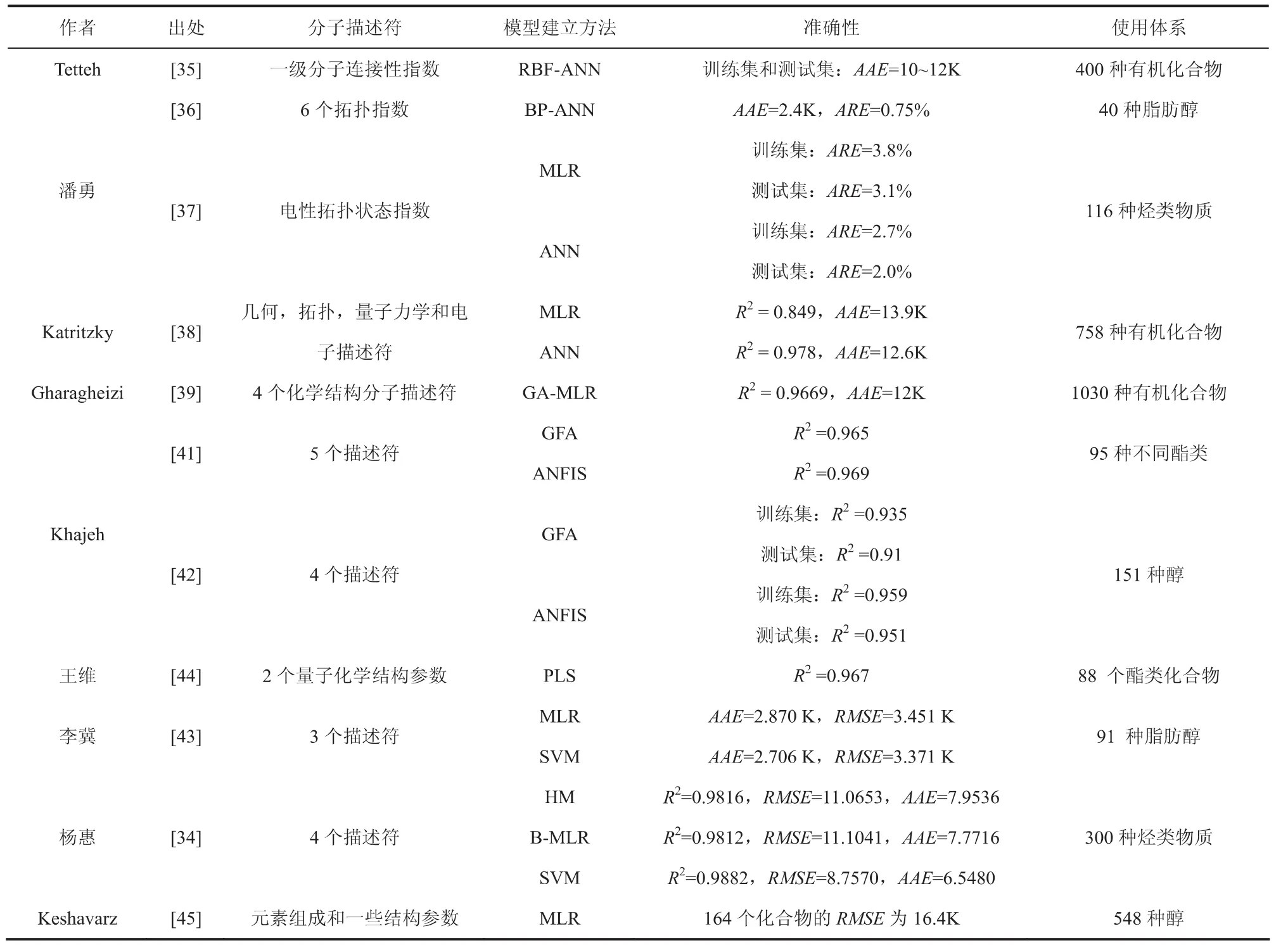
表1 纯组分QSPR模型预测结果

Tetteh等人[35]以一级分子连接性指数为分子描述符，建立了基于25个官能团的400种化合物径向基函数（RBF）神经网络模型。潘勇等人[36]根据分子结构的特点，提出一组拓扑指数作为表征物质结构特征的分子结构描述符，利用基于误差反向传播(Back-Propagation,BP)算法的人工神经网络用于脂肪醇的闪点预测；另外，潘勇等人[37]建立了一个应用电性拓扑状态指数(ETSI)预测116种烃类物质闪点的定量结构-性质相关性(QSPR)研究模型。分别采用线性回归分析法和人工神经网络法对所研究化合物的闪点与其分子结构之间的定量关系进行研究。训练集的线性回归方法和神经网络方法的平均相对误差分别为3.8%和2.7%；测试集的2种方法的平均相对误差分别为3.1%和2.0%。实验结果表明，无论是线性回归分析法还是人工神经网络法，闪点预测值与实验值均符合良好，优于传统基团贡献法所得结果。ANN方法建立的是一种“黑箱”模型，不能给出直观的数学模型，因而无法准确了解各结构参数对模型的贡献值，而这些正是线性回归模型的优势。因此，MLR和ANN这两种方法各有利弊，并存在一定的互补性。

Katritzky等人[38]使用几何、拓扑、量子力学和电子描述符来模拟758种有机化合物的闪点。在该模型中出现的描述符也具有物理意义，主要是涉及静电和氢键相互作用以及分子形状，除了多元线性模型外（R2=0.849，平均误差13.9K），还使用人工神经网络的方法进行了预测（R2=0.978，平均误差12.6K）。

Gharagheizi[39,40]采用QSPR模型和基于遗传算法的多元线性回归（GFA-MLR）技术，选取4个化学结构为基础的分子描述符，预测1030个有机化合物的闪点。Khajeh[41,42]建立了基于不同酯类和醇类的闪点预测模型，利用遗传函数逼近（GFA）方法从1124个描述符中选择四或五个最重要的分子描述符，作为自适应神经模糊推理系统（ANFIS）的输入参数，建立了QSPR模型。这些分子描述符，具体量化说明了分子的结构多样性、对称性、复杂性对闪点的影响。李冀等人[43]应用 Dragon软件，利用遗传函数算法 (GFA)从1481个描述符中筛选出3个与脂肪醇闪点关系最密切的分子描述符，分别用多元线性回归(MLR)方法和支持向量机(SVM)方法进行建模，并采用内部验证和外部检验的方式对模型的拟合度、预测性等性能进行验证。

王维等人[44]对88个酯类化合物进行了B3LYP/6-31G*水平上的结构优化，并在优化结构基础上进行了量子化学结构参数的计算，应用偏最小二乘法(PLS)对酯类化合物闪点与量子化学参数（分子热力学自由能(ΔG)结合偶极距(μ)）进行了关联。结果表明分子热力学自由能与化合物闪点温度呈负相关，而偶极距和酯类化合物的闪点呈正相关性，这是因为分子极性(偶极距)越大，范德华相互作用越大，同时酯类化合物形成氢键的能力也越大。Keshavarz等人[45]基于元素组成和一些结构参数，研究了不同分子结构的醇类和酚类化合物，即无环醇类和环状醇类以及具有脂肪族-芳香族复合结构的酚类和醇类。作者考虑了校正因子(CF)（包括特定分子内吸引力、分支、较重原子和长链烷）对闪点的影响。

杨惠[34]用CODESSA软件中的HM方法和B-MLR方法来筛选374种分子结构描述符，最终得到与烃类物质闪点密切相关的4个描述符，进行线性拟合；利用支持向量机(SVM)的研究直接采用B-MLR方法筛选出的分子描述符作为输入参数建立非线性模型。在HM、B-MLR和SVM三种方法所建立的闪点预测模型中，SVM模型的效果最佳，不仅揭示了烃类物质闪点与其分子结构间可能存在较强的非线性关系，也说明了将SVM应用于QSPR研究的优越性，它能有效地解决小样本、非线性、过拟合、维数灾难和局部极小等问题，并具有较强的泛化推广性能。但SVM不能给出直观的数学表达式，因而很难直接根据预测模型准确地了解和掌握各结构参数对闪点的影响程度和规律。

2 闪点计算与预测模型的特点与发展

闪点(FP)是易燃液体及其分类标准的重要划分依据，同时也是衡量可燃液体火灾危险性的重要参数。为弥补实验测定的不足，借助模型预测来计算闪点具有重要的理论意义和实用价值。通过分析归纳，易燃液体闪点的估算方法主要分为三类:经验关联计算，基团贡献法计算和基于分子结构的模型预测，三类方法具有各自的优势和特点。

闪点的经验关联计算是从可靠的实验数据出发，依据相关的物理性质如沸点、密度和汽化焓等，利用数学手段（线性拟合、非线性拟合等）构建相应的关联式。其优势在于此方法直观简单，便于理解和计算，而不足之处在于此方法不适用于预测基础物理性质未知的物质闪点，因为对于设计合成具有一定功能和特定基团的有机物而言，有结构的设想，但没有具体物理性质如沸点、密度和汽化焓等的数据，因此无法获知其相应的闪点预测值。

基团贡献法计算闪点是基于有机物所包含的官能团种类及数量，依据各官能团对闪点的贡献，再利用数学模型（线性函数模型、非线性函数模型、人工神经网络等）来预测物质的性质。人工神经网络能够从分子结构的角度预测纯化合物的闪点，推测对纯化合物闪点有重要贡献的结构基团，具有一定的优势。然而，由于异构体具有相同数量和种类的基团，使得计算结果不可避免地相同，因此大多数基团贡献方法无法区分结构异构体的性质差异。近年来，基团贡献法的发展是将基于分子结构的基团贡献与有机物物理性质如沸点等进行结合，利用非线性拟合得到模型，可以用于分辨结构异构体闪点性质的差异。

定量结构-性质关系的方法已成为研究的热点之一，因其不需要任何物理性质，直接通过分子结构特点来预测新物质的闪点，受到广泛关注。此方法的关键在于分子描述符的计算与选择，因分子描述符的计算与选择过程非常繁琐，需要借助计算分子描述符的专门软件，同时分子描述符对分子结构信息表征不足将会影响预测模型的精度。今后对有机物的分子结构特征进行更为全面、有效的表征，将量子化学描述符、结构化学描述符引入进行丰富分子描述符，将得到更为精细的分子结构信息，会大大提高预测模型的精度。

以上三种方法预测闪点各有其优势和特点，并存在一定的互补性，借用各模型的优势来预测闪点的研究受到广泛关注。借助于实验数据和理论模型的优势，为有机物闪点的预测提供了一个快速简便的有效途径。